高中 | 带电粒子在交变电场中的运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在交变电场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在交变电场中的运动
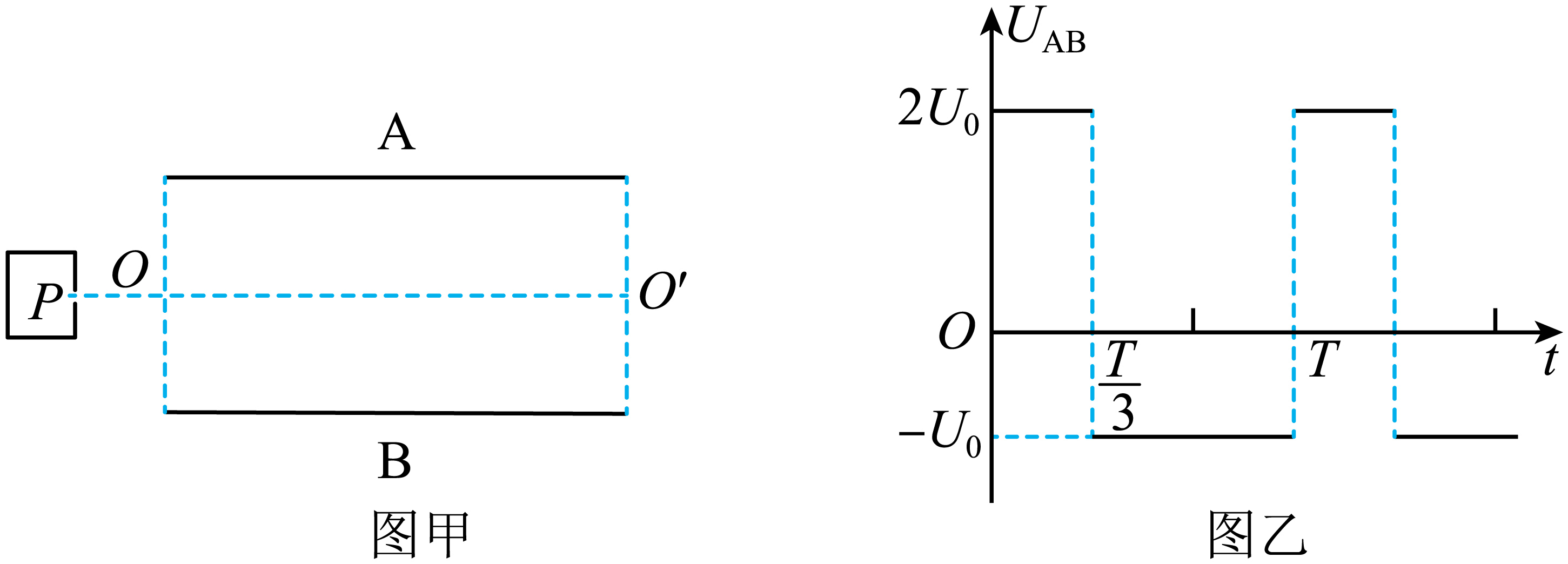
如图甲所示,两水平放置的平行导体板$A$、$B$,板长为$L$,板间距离为$d$,$OO'$为两板中心线,两板间加上有周期性变化的电压$U_{AB}$,如图乙所示(图中$T$为已知值,$U_{0}$为未知值)。左侧$P$为粒子源,源源不断地发出质量为$m$、带电量为$q(q\gt0)$的带电粒子,粒子均以相同的初速度从$O$点水平射入两板间。若带电粒子在$t=0$时刻从$O$点射入平行板,$T$时刻刚好从$B$板的右边缘射出。带电粒子的重力、粒子间相互作用均忽略不计,两板间电场为理想的匀强电场。求:
带电粒子射入平行板的初速度;
$\\dfrac{L}{T}$
"]]由题可知,粒子在电场中沿水平方向做匀速直线运动,故粒子进入平行板的初速度$v_{0}=\dfrac{L}{T}$
图乙中$U_{0}$的值;
$\\dfrac{3md^{2}}{2qT^{2}}$
"]]粒子在平行板竖直方向做匀加速运动,$0 \sim \dfrac{T}{3}$粒子的加速度为$a_{1}$,根据牛顿第二定律可得$\dfrac{q \cdot 2U_{0}}{d}=ma_{1}$
解得$a_{1}=\dfrac{2qU_{0}}{md}$
方向竖直向下,此阶段沿竖直方向偏转的位移$y_{1}=\dfrac{1}{2}a_{1}{\left(\dfrac{T}{3}\right)}^{2}=\dfrac{qU_{0}T^{2}}{9md}$
此时粒子沿竖直方向的速度$v_{y}=a_{1} \cdot \dfrac{T}{3}=\dfrac{2qU_{0}T}{3md}$
$\dfrac{T}{3} \sim T$时间内,粒子竖直方向的加速度为$a_{2}$,根据牛顿第二定律则有$\dfrac{qU_{0}}{d}=ma_{2}$
解得$a_{2}=\dfrac{qU_{0}}{md}$
方向竖直向上,此阶段粒子在竖直方向做匀减速直线运动,偏转位移为$y_{2}=v_{1} \cdot \left(\dfrac{2T}{3}\right)-\dfrac{1}{2}a_{2}{\left(\dfrac{2}{3}T\right)}^{2}=\dfrac{2qU_{0}T^{2}}{9md}$
根据题意可得$y_{1}+y_{2}=\dfrac{d}{2}$
联立解得$U_{0}=\dfrac{3md^{2}}{2qT^{2}}$
$0 \sim \dfrac{T}{3}$时间内$t_{0}$时刻射入平行板的粒子恰好从$O'$点射出,求$t_{0}$。
$\\dfrac{T}{6}$
"]]粒子在$t_{0}$时刻进入平行板,$t_{0} \sim \dfrac{T}{3}$粒子在竖直方向的加速度为$a_{1}=\dfrac{2qU_{0}}{md}$
竖直方向上的位移$y_{1}'=\dfrac{1}{2}a_{1}{\left(\dfrac{T}{3}-t_{0}\right)}^{2}$
此时粒子的速度$v_{1}'=\dfrac{2qU_{0}}{md} \cdot\left(\dfrac{T}{3}-t_{0}\right)$
粒子在$\dfrac{T}{3} \sim T$的时间内,其加速度$a_{2}=\dfrac{qU_{0}}{md}$
此阶段的位移$y_{2}'=v_{1}' \cdot \left(\dfrac{2T}{3}\right)-\dfrac{1}{2}a_{2}{\left(\dfrac{2}{3}T\right)}^{2}$
$T$末时刻粒子的速度$v_{2}=v_{1}'-a_{2}\left(\dfrac{2}{3}T\right)$
设经过$t$时间粒子到达$O'$,此阶段粒子的加速依然为$a_{1}=\dfrac{2qU_{0}}{md}$
此阶段竖直方向的位移$y_{3}=v_{2}t_{0}+\dfrac{1}{2}a_{1}t_{0}^{2}$
由于在竖直方向位移为零,即$y_{1}'+y_{2}'+y_{3}=0$
联立解得$t_{0}=\dfrac{T}{6}$
高中 | 带电粒子在交变电场中的运动题目答案及解析(完整版)
