高中 | 带电粒子在交变电场中的运动 题目答案及解析
稿件来源:高途
高中 | 带电粒子在交变电场中的运动题目答案及解析如下,仅供参考!
选修3-1
第一章 静电场
1.9 带电粒子在电场中的运动
带电粒子在交变电场中的运动
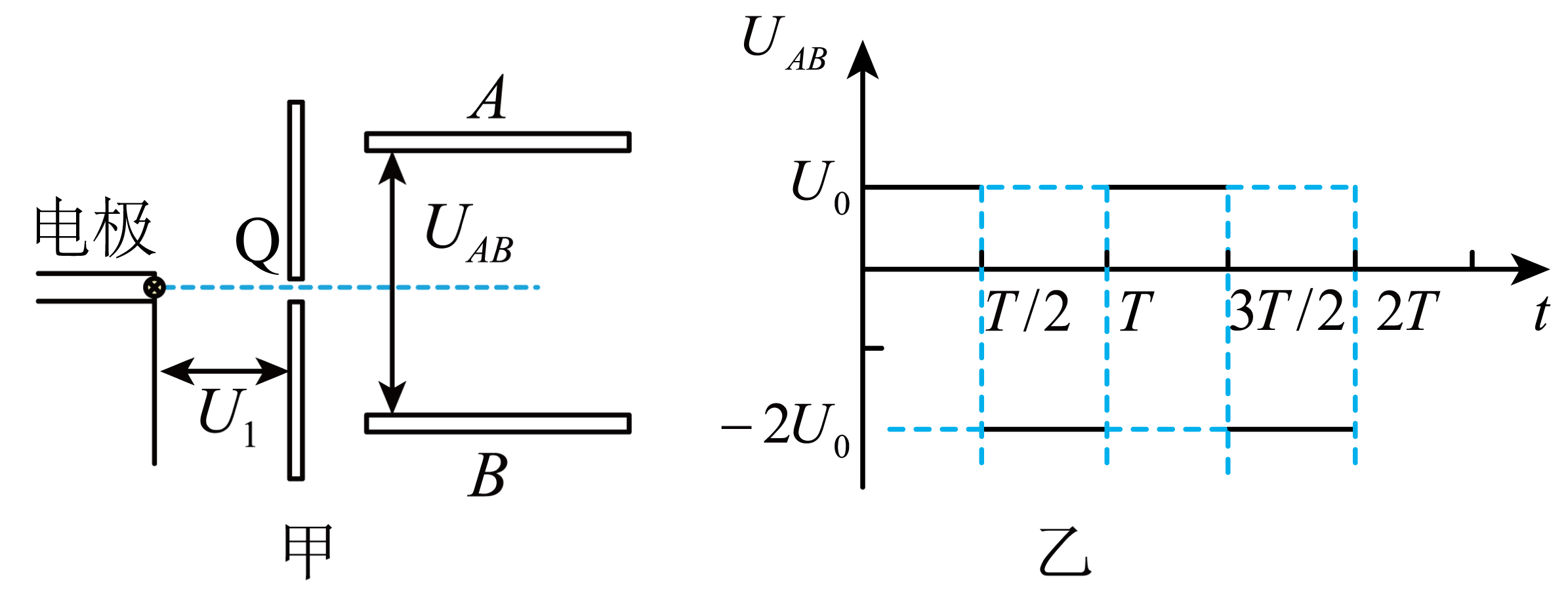
如图甲所示,真空中的电极可连续不断地均匀飘出电子(电子的初速度可视为零)。电子经电场加速后,由小孔$Q$穿出并沿平行板电容器中轴线射入偏转电场,$AB$两板间距为$d$,板长为$2L$,两板间加周期性变化的电压$U_{AB}$如图乙所示,已知加速电压为$U_{1}=\dfrac{2mL^{2}}{eT^{2}}$,电子质量为$m$,电量为$e$,$T$为偏转电场的周期,图中$U_{0}$为已知量。不计电子的重力,不计电子间的相互作用力,且所有电子都能离开偏转电场,求:
电子从加速电场$U_{1}$飞出后的水平速度$v_{0}$大小?
$\\dfrac{2L}{T}$
"]]粒子在加速电场中则$U_{1}e= \dfrac{1}{2}mv_{0}^{2}$
其中$U_{1}=\dfrac{2 mL^{2}}{eT^{2}}$
解得$v_{0}=\dfrac{2L}{T}$
$t=0$时刻射入电容器的电子离开电场时偏离$AB$中轴线的距离$y$;
$\\dfrac{U_{0}eT^{2}}{8md}$
"]]粒子在偏转电场中水平方向匀速运动,则时间$t=\dfrac{2L}{v_{0}}=T$
加速度$a_{1}=\dfrac{U_{0}e}{md}$
则$0 \sim \dfrac{T}{2}$竖直位移$y_{1}=\dfrac{1}{2}a_{1}{\left(\dfrac{T}{2}\right)}^{2}=\dfrac{U_{0}eT^{2}}{8md}$
$\dfrac{T}{2} \sim T$时间内做减速运动,加速度$a_{2}=\dfrac{2U_{0}e}{md}=2a_{1}$
则$y_{2}=\left(a_{1}\dfrac{T}{2}\right)\dfrac{T}{2}-\dfrac{1}{2}a_{2}{\left(\dfrac{T}{2}\right)}^{2}=0$
电子离开电场时偏离$AB$中轴线的距离$y=y_{1}+y_{2}=\dfrac{U_{0}eT^{2}}{8md}$
在足够长的时间内从中线上方离开偏转电场的电子占电子总数的比值。
$\\dfrac{1}{6}$
"]]设从$t_{1}$时刻进入电容器。$\dfrac{1}{2}a_{1}{\left(\dfrac{T}{2}-t_{1}\right)}^{2}+\left\{ a_{1}\left( \dfrac{T}{2}-t_{1} \right)\dfrac{T}{2}-\dfrac{1}{2}2a_{1}{\left(\dfrac{T}{2}\right)}^{2}\right\}+\left\{ \left(-\dfrac{T}{2}a_{1}-a_{1}t_{1} \right)t_{1}+\dfrac{1}{2}a_{1}t_{1}^{2} \right\}=0$
可得$t_{1}=\dfrac{T}{12}$
设从$T$时刻前的一段时间$t_{2}$进入电容器。$\dfrac{1}{2} \times 2a_{1}t_{2}^{2}+\left\{ 2a_{1}t_{2}\dfrac{T}{2}-\dfrac{1}{2}a_{1}{\left(\dfrac{T}{2}\right)}^{2}\right\}+\left\{\left( 2a_{1}t_{2}-a_{1}\dfrac{T}{2} \right)\left( \dfrac{T}{2}-t_{2} \right)+\dfrac{1}{2} \times 2a_{1}{\left(\dfrac{T}{2}-t_{2}\right)}^{2}\right\}=0$
$t_{2}=\dfrac{T}{12}$
综上,在足够长的时间内从中线上方离开偏转电场的电子占电子总数的比值为$\dfrac{\dfrac{T}{12}+\dfrac{T}{12}}{T}=\dfrac{1}{6}$
高中 | 带电粒子在交变电场中的运动题目答案及解析(完整版)
