如图所示，甲、乙两小球带电量的绝对值均为$q$，甲用绝缘支架固定，质量为$m$的乙用轻质绝缘细线悬挂在横杆上，当两球处于静止状态时，两球心等高，两球心的连线，悬点与两球心的连线构成等边三角形。已知静电力常量为$k$，重力加速度为$g$，两球均视为质点和点电荷，下列说法正确的是$(\qquad)$

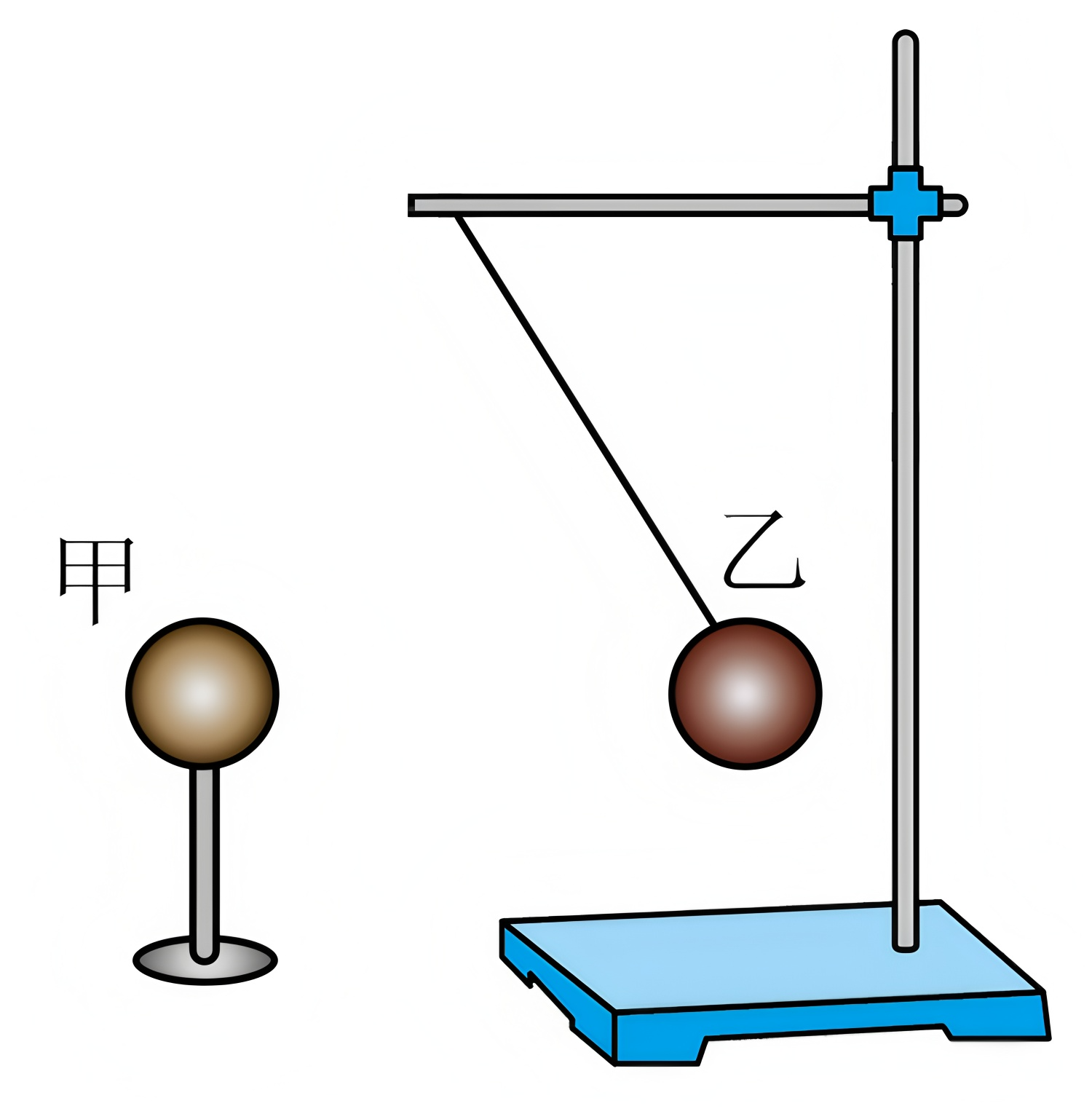
两球均带正电

甲的质量为$\\sqrt{3}m$

细线的拉力为$\\sqrt{3}mg$

细线的长度为$q\\sqrt{\\dfrac{\\sqrt{3}k}{mg}}$

$\rm A$．通过受力分析可知，两球之间的相互作用力为斥力，所以两球带同种电荷，可均带正电，也可均带负电，$\rm A$错误；

$\rm B$．被绝缘支架固定，虽处于受力平衡状态，因支架对甲的作用力未知，故无法求出甲的质量，$\rm B$错误；

$\rm C$．对乙受力分析，由三力平衡的矢量三角形可得$\dfrac{mg}{T}=\sin 60{^\circ}$，$\dfrac{F_{斥}}{mg}=\tan 30{^\circ}$

解得$T=\dfrac{2\sqrt{3}}{3}mg$，$F_{斥}=\dfrac{\sqrt{3}mg}{3}$

$\rm C$错误；

$\rm D$．由$F_{斥}=\dfrac{kq^{2}}{L^{2}}=\dfrac{\sqrt{3}mg}{3}$

解得两球心间的距离$L=q\sqrt{\dfrac{\sqrt{3}k}{mg}}$

则细线的长度为$L=q\sqrt{\dfrac{\sqrt{3}k}{mg}}$

$\rm D$正确。

故选：$\rm D$。