如图所示质量为$3m$、电荷量为$q$的带电小球$A$用绝缘细线悬挂于$O$点，带有电荷量为$Q$的小球$B$固定在$O$点正下方绝缘柱上。其中$O$点与小球$A$的间距为$l$。$O$点与小球 $B$的间距为$\sqrt{3}l$，当小球$A$平衡时，悬线与竖直方向夹角$\theta=30^\circ $，带电小球$A$、$B$均可视为点电荷，静电力常量为$k$，则$(\qquad)$

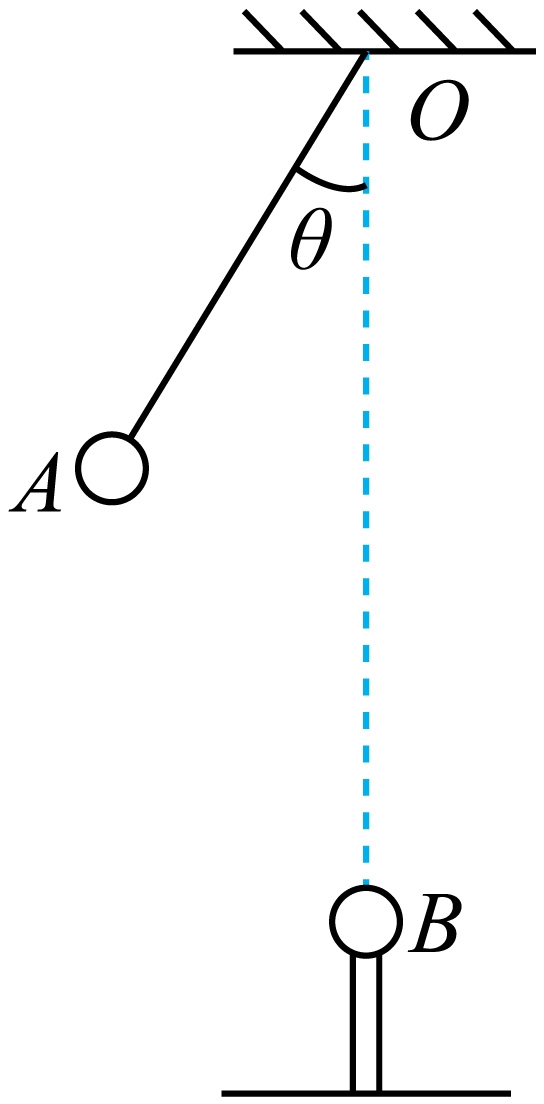
$A$、$B$间库仑力大小$F=\\dfrac{kq^{2}}{2l^{2}}$

$A$、$B$间库仑力$F=\\dfrac{\\sqrt{3}mg}{3}$

小球$B$的带电量为$\\dfrac{\\sqrt{3}mgl^{2}}{3kq}$

细线拉力大小$F_{\\text{T}}=\\sqrt{3}mg$

$\rm D$．$A$的受力如图所示

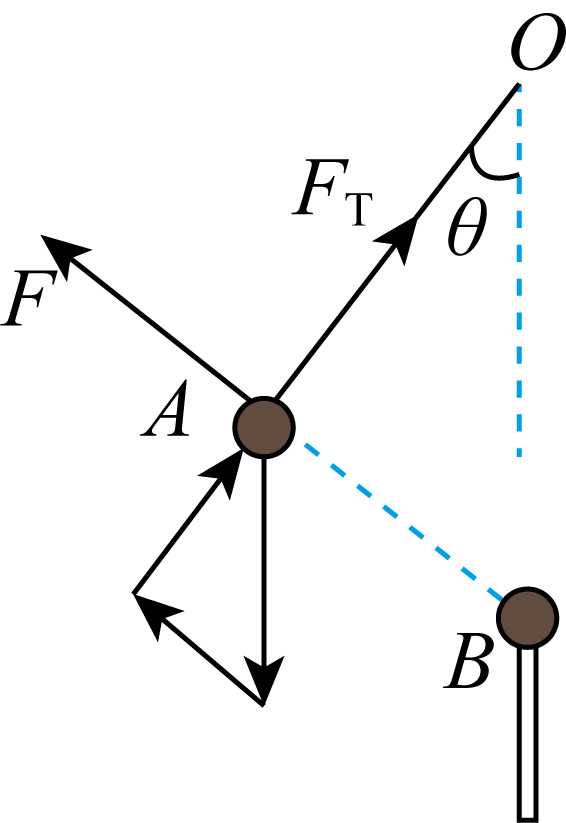
几何三角形$OAB$与力三角形相似，由对应边成比例$\dfrac{F_{\text{T}}}{3mg}=\dfrac{l}{\sqrt{3}l}$

解得$F_{\text{T}}=\sqrt{3}mg$

故$\rm D$正确；

$\rm ABC$．由余弦定律得$AB=\sqrt{l^{2}+{(\sqrt{3}l)}^{2}-2\sqrt{3}l^{2}\cos 30{^\circ}}=l$

几何三角形$OAB$与力三角形相似，由对应边成比例$\dfrac{F_{\text{T}}}{F}=\dfrac{l}{AB}$

可得$F_{\rm T}=F=k\dfrac{Qq}{l^{2}}$

解得$Q=\dfrac{\sqrt{3}mgl^{2}}{kq}$

故$\rm ABC$错误。

故选：$\rm D$。