如图所示的装置装有一根羽毛与一个金属小球，该装置可在地球上重现斯科特的实验，将管倒置，向外拉动注射器活塞，羽毛竖直下落的加速度大小将                 （选涂：$\rm A$．变大    $\rm B$．不变    $\rm C$．变小）；

上述实验现象在地球上重现，原因是排除了空气阻力的影响；将管倒置，向外拉动注射器活塞，羽毛因为失去空气阻力的影响，根据$mg − f=ma$可知，其加速度大小将变大；

故选：$\rm A$；

伽利略在对落体运动的研究过程中开创的科学研究方法可以用下面的流程图表示：

则方框$1$和$2$中的方法和对应内容存在不正确的是有$(\qquad)$

$1$是猜想假设：落体运动的速度$v$和时间$t$成正比

$1$是数学推演：落体运动的位移$x$和时间的平方$t^{2}$成正比

$2$是得出结论：落体运动的速度$v$和时间$t$成正比

$2$是得出结论：落体运动的位移$x$和时间的平方$t^{2}$成正比

$\rm AB$．提出问题后$1$是猜想假设：落体运动的速度$v$和时间$t$成正比，故$\rm A$正确，不符合题意，$\rm B$错误，符合题意；

$\rm CD$．$2$是得出结论：小球沿光滑斜面运动的位移$x$和时间的平方$t^{2}$成正比，故$\rm CD$错误，符合题意；

故选：$\rm BCD$；

如图所示，甲突然释放刻度尺，乙迅速夹住，由此判断乙的反应时间。现在尺上贴上间隔$0.02\;\rm s$的刻度制成反应时间尺。下列说法正确的是$(\qquad)$

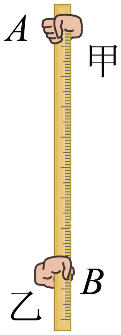
反应时间尺的“$0$”刻度位于$A$处

反应时间尺的刻度疏密均匀

反应时间尺的刻度$A$处较密

反应时间尺的刻度$B$处较密

$\rm A$．反应时间为零指的是甲一释放刻度尺，乙就夹住，刻度尺并未下落，故反应时间尺的“$0$”刻度位于$B$处，故$\rm A$错误；

$\rm BCD$．做匀加速直线运动的物体，相同时间内的位移逐渐增大，即随着刻度尺的下落，每隔$0.02\;\rm s$的位移逐渐增大，可知反应时间尺的刻度疏密不均匀，反应时间尺的刻度$B$处较密，$A$处较疏，故$\rm BC$错误，$\rm D$正确；

故选：$\rm D$；

如图所示，$AB$为空心圆管，长度为$L=10\:\rm m$，$ C$为可视为质点的小球，$B$与$C$在同一竖直线上。$A$、$C$之间距离为$h=20\:\rm m$。$t=0$时刻，由静止释放圆管$AB$。同时小球$C$从地面以初速度$v_{0}$竖直向上抛出。忽略空气阻力，圆管$AB$若落地，则立即静止，取$g=10\;\rm m/s^{2}$。要使小球$C$在圆管$AB$落地前从$B$端穿出，$v_{0}$至少为                 $\;\rm m/s$；若$v_{0}=20\;\rm m/s$，则小球$C$从$A$端进入管中至由$B$端穿出所经过的时间$\Delta t$为                 $\;\rm s$；

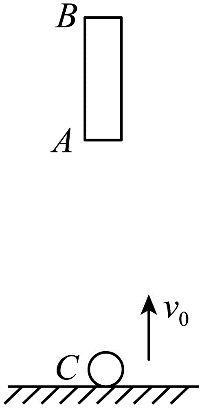
根据题意，由公式$h= \dfrac{1}{2}gt^{2}$可得，$AB$落地时间为$t=2\;\rm s$，要使$C$在$AB$落地前从$B$端穿出，则有$v_{0}t-\dfrac{1}{2}gt^{2} \geqslant L$，代入数据解得$v_{0}\geqslant 15\;\rm m/s$

若$v_{0}=20\;\rm m/s$，设$C$从$B$端穿出时运动的时间为$t_{1}$，$C$从$A$端穿入时运动的时间为$t_{2}$，则有$\dfrac{1}{2}gt_{1}^{2}+v_{0}t_{1}-\dfrac{1}{2}gt_{2}^{2}=L+h$、$\dfrac{1}{2}gt_{2}^{2}+v_{0}t_{2}-\dfrac{1}{2}gt_{2}^{2}=h$，则$C$从$A$端进入管中至由$B$端穿出所经过的时间为$t=t_{1} − t_{2}$，联立代入数据解得$t=0.5\;\rm s$；

如图（$a$）所示，将质量为$m$的小球在长为$l$、倾角为$\theta$的光滑斜面最上端由静止释放。（重力加速度为$g$）请借助此模型，通过数学推演证明：如图（$b$）所示的实验中理想斜面倾角$\theta$越小，越容易测量时间。

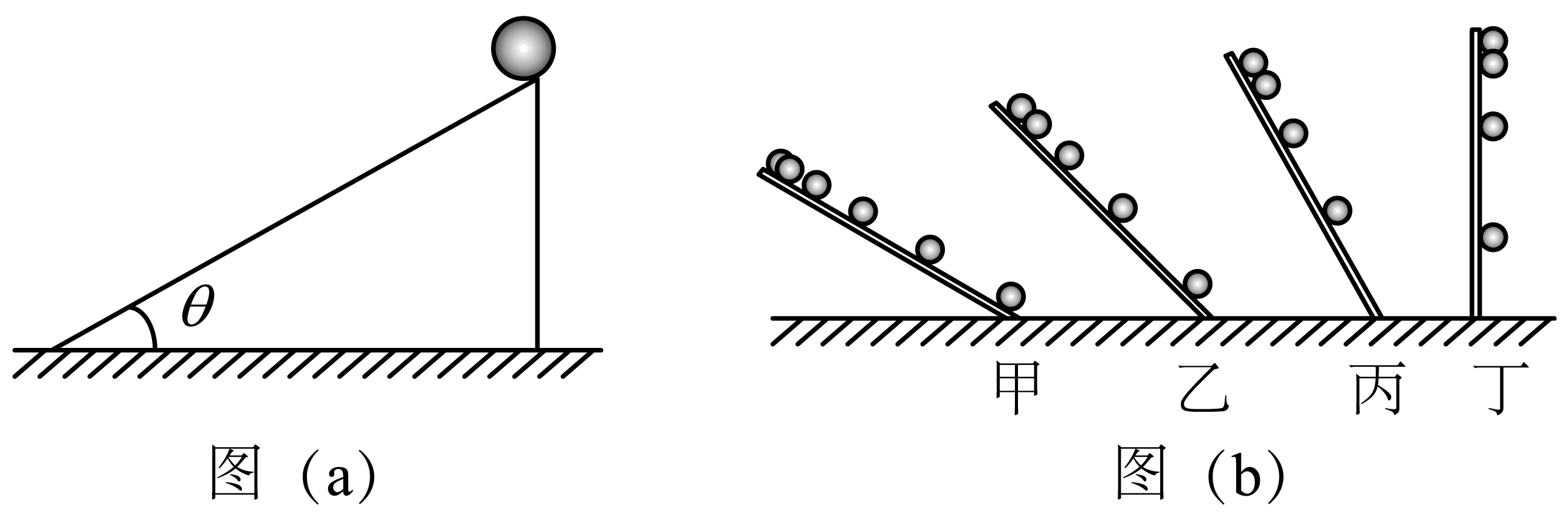
见解析

对小球进行受力分析，如图所示

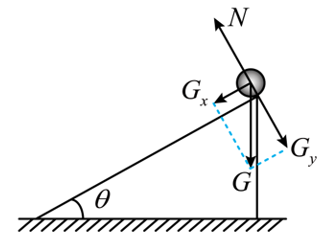
沿斜面方向正交分解可知，水平方向有$mg\sin \theta=ma$，即$a=g\sin \theta$，由于$l=\dfrac{1}{2}at^{2}$，可得$t=\sqrt{\dfrac{2l}{g\sin\theta}}$，$\theta$越小，$t$越大，越容易测量。