如图所示，足够长的传送带与水平面的夹角为$\theta$，速率恒为$v_{0}$，宽为$d$的$MNQP$区域存在与传送带平面垂直向上的匀强磁场，磁感应强度大小为$B$。边长为$l(l \lt \dfrac{d}{2})$、质量为$m$、电阻为$R$的正方形线框$efgh$置于传送带上，进入磁场前与传送带保持相对静止，线框$ef$边刚离开磁场区域时的速率恰为$v_{0}$。若线框$ef$或$gh$边受到安培力，则其安培力大于$2mg\sin\theta$。线框受到的最大静摩擦力等于滑动摩擦力，动摩擦因数$\mu =\tan\theta$，$ef$边始终平行于$MN$，重力加速度为$g$。下列选项正确的是$(\qquad)$

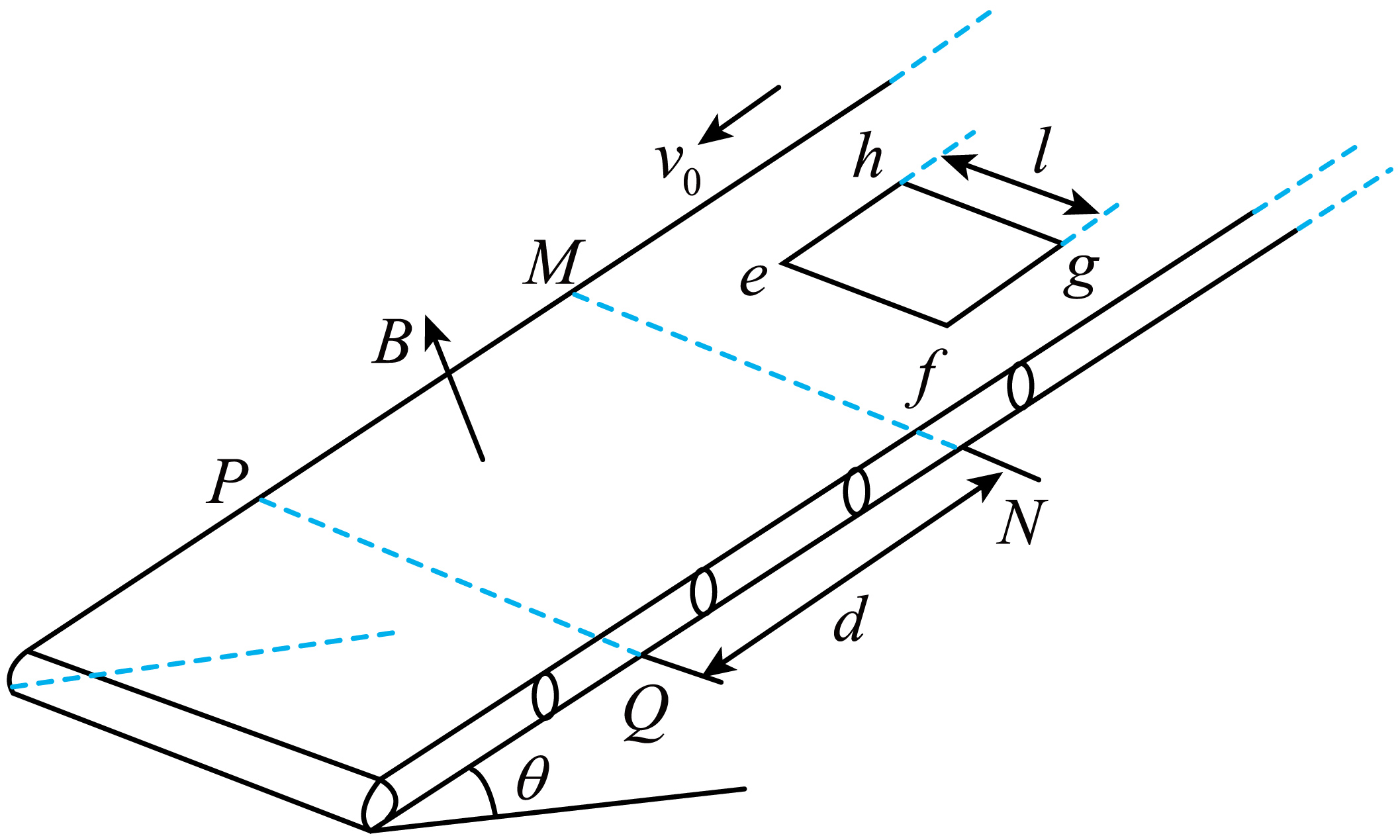
线框速率的最小值为$\\sqrt{v_{0}^{2}-4g(d-l)\\sin\\theta}$

线框穿过磁场区域产生的焦耳热为$2mgd\\sin \\theta$

线框穿过磁场区域的时间为$\\dfrac{B^{2}l^{3}+mR\\left( \\sqrt{v_{0}^{2}-4g(d-l)\\sin\\theta}-v_{0} \\right)}{2mgR\\sin\\theta}$

$ef$边从进入到离开磁场区域的时间内，传送带移动距离为$\\dfrac{B^{2}l^{3}v_{0}}{2mgR\\sin\\theta}$

$\rm A$．在$ef$边进入磁场而$gh$边未进入磁场的过程中，线框受到沿传送带平面向上的安培力$BIL$和沿传送带平面向下的重力分力$mg\sin \theta$。若线框相对传送带滑动，则滑动摩擦力为$\mu mg\cos \theta$，而$\mu =\tan \theta$，故$\mu mg\cos \theta=mg\sin \theta$

已知线框受到的安培力$BLI \gt 2mg\sin \theta$

即$BIL \gt mg\sin \theta+\mu mg\cos \theta$

因此线框将相对传送带向上滑动，滑动摩擦力方向沿传送带平面向下。线框在沿传送带平面的安培力、重力分力、摩擦力作用下做减速运动。在$gh$边进入磁场到$ef$边离开磁场的过程中，因线框速度小于传送带速度，故其所受滑动摩擦力方向沿传送带平面向下。又因线框不受安培力，所以其在沿传送带平面的滑动摩擦力和重力分力作用下做匀加速直线运动。综上分析可知，当$gh$边刚进入磁场时，线框有最小速度$v_{\min}$。设线框加速度为$a$，根据牛顿第二定律有$mg\sin \theta+\mu mg\cos \theta=ma$

$ef$边离开磁场时速度恰好为$v_{0}$，则有$v_{0}^{2} − v_{\min}^{2}=2a(d − l)$

联立解得$v_{\min}=\sqrt{v_{0}^{2}-4g(d-l)\sin\theta}$，故$\rm A$正确；

$\rm B$．在$ef$边进入磁场到$gh$边进入磁场的过程中，由动能定理有$mgl\sin\theta+\mu mgl\cos\theta+W_{安}=\dfrac{1}{2}mv_{\min}^{2}-\dfrac{1}{2}mv_{0}^{2}$

则该过程产生的焦耳热$Q=−W_{安}=2mgd\sin \theta$

在$ef$边离开磁场到$gh$边离开磁场的过程中，线框产生的焦耳热也为$Q$。因此，线框穿过磁场区域产生的焦耳热为$4mgd\sin \theta$，故$\rm B$错误；

$\rm C$．设$ef$边进入磁场到$gh$边进入磁场的时间为$t_{1}$，根据闭合电路欧姆定律得$I=\dfrac{BLv}{R}$

根据动量定理有$mg\sin \theta ⋅ t_{1}+\mu mg\cos \theta ⋅ t_{1} − ∑BIL\Delta t=mv_{\min} − mv_{0}$

设$gh$边进入磁场到$ef$边离开磁场的时间为$t_{2}$，有$v_{0} − v_{\min}=at_{2}$

因为$ef$边离开磁场到$gh$边离开磁场所用时间也为$t_{1}$，所以线框穿过磁场区域的总时间$t=2t_{1}+t_{2}$

联立解得$t=\dfrac{2B^{2}l^{3}+mR\left( \sqrt{v_{0}^{2}-4g(d-l)\sin\theta}-v_{0} \right)}{2mgR\sin\theta}$，故$\rm C$错误；

$\rm D$．$ef$边从进入到离开磁场区域的时间$t^{^\prime}=t_{1}+t_{2}$

该段时间内传送带移动的距离$s=v_{0}t^{'}=\dfrac{B^{2}l^{3}v_{0}}{2mgR\sin\theta}$，故$\rm D$正确。

故选：$\rm AD$。