高中 | 牛顿第二定律的两类基本问题 题目答案及解析
稿件来源:高途
高中 | 牛顿第二定律的两类基本问题题目答案及解析如下,仅供参考!
必修1
第四章 牛顿运动定律
4.6 用牛顿运动定律解决问题(一)
牛顿第二定律的两类基本问题
如图$1$所示,细杆两端固定,质量为$m$的物块穿在细杆上。初始时刻。物块刚好能静止在细杆上。现以水平向左的力$F$作用在物块上,$F$随时间$t$的变化如图$2$所示。开始滑动瞬间的滑动摩擦力等于最大静摩擦力。细杆足够长,重力加速度为$g$,$\theta=30^\circ$。
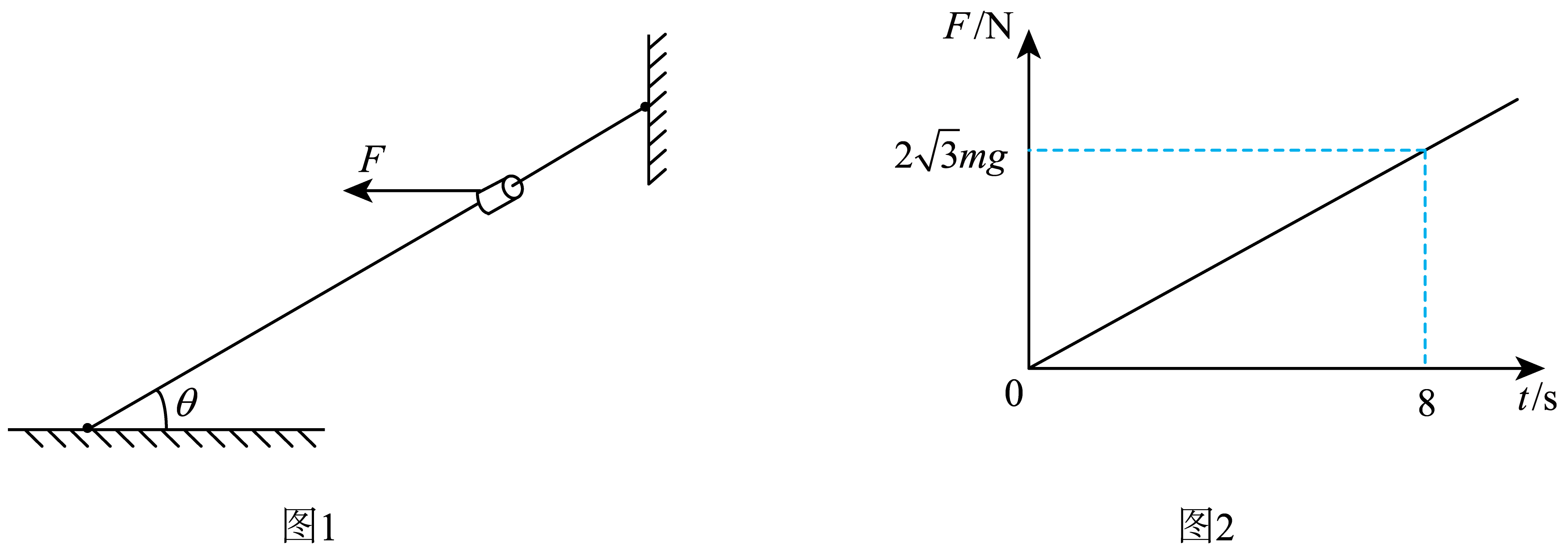
求:
$t=6\;\rm s$时$F$的大小,以及$t$在$0$~$6\;\rm s$内$F$的冲量大小。
$F= \\dfrac{3\\sqrt{3}mg}{2}$,$\\dfrac{9\\sqrt{3}mg}{2}$
"]]由图$2$可知$F$随时间线性变化,根据数学知识可知$F=\dfrac{\sqrt{3}mg}{4}t$
所以当$t=6\;\rm s$时,$F=\dfrac{3\sqrt{3}mg}{2}$
$0$~$6\;\rm s$内$F$的冲量为$F$−$t$图围成的面积,即$I=\dfrac{1}{2} \times \dfrac{3\sqrt{3}}{2}mg \times 6=\dfrac{9\sqrt{3}}{2}mg$
$t$在$0\sim 6\;\rm s$内,摩擦力$f$随时间$t$变化的关系式,并作出相应的$f−t$图像。
见解析
"]]由于初始时刻。物块刚好能静止在细杆上,则有$mg\sin 30^\circ =\mu mg\cos 30^\circ $
即$\mu=\tan 30^{{^\circ}}=\dfrac{\sqrt{3}}{3}$
在垂直杆方向,当$F\sin \theta=mg\cos \theta$时,$t=4\;\rm s$
则$0-4\;\rm s$,垂直杆方向$F\sin \theta+N=mg\cos \theta$
摩擦力$f=\mu N=\dfrac{\sqrt{3}}{3}\left( \dfrac{\sqrt{3}}{2}mg-\dfrac{\sqrt{3}}{8}mgt \right)=\left( \dfrac{1}{2}-\dfrac{1}{8}t \right)mg$ $(0 ≤ t ≤ 4)$
在$4-6\;\rm s$内,垂直杆方向$F\sin \theta=mg\cos \theta+N$
摩擦力$f=\mu N=\dfrac{\sqrt{3}}{3}\left( \dfrac{\sqrt{3}}{8}mgt-\dfrac{\sqrt{3}}{2}mg \right)=\left( \dfrac{1}{8}t-\dfrac{1}{2} \right)mg$ $(4 ≤ t ≤ 6)$
相应的$f$−$t$图像如图
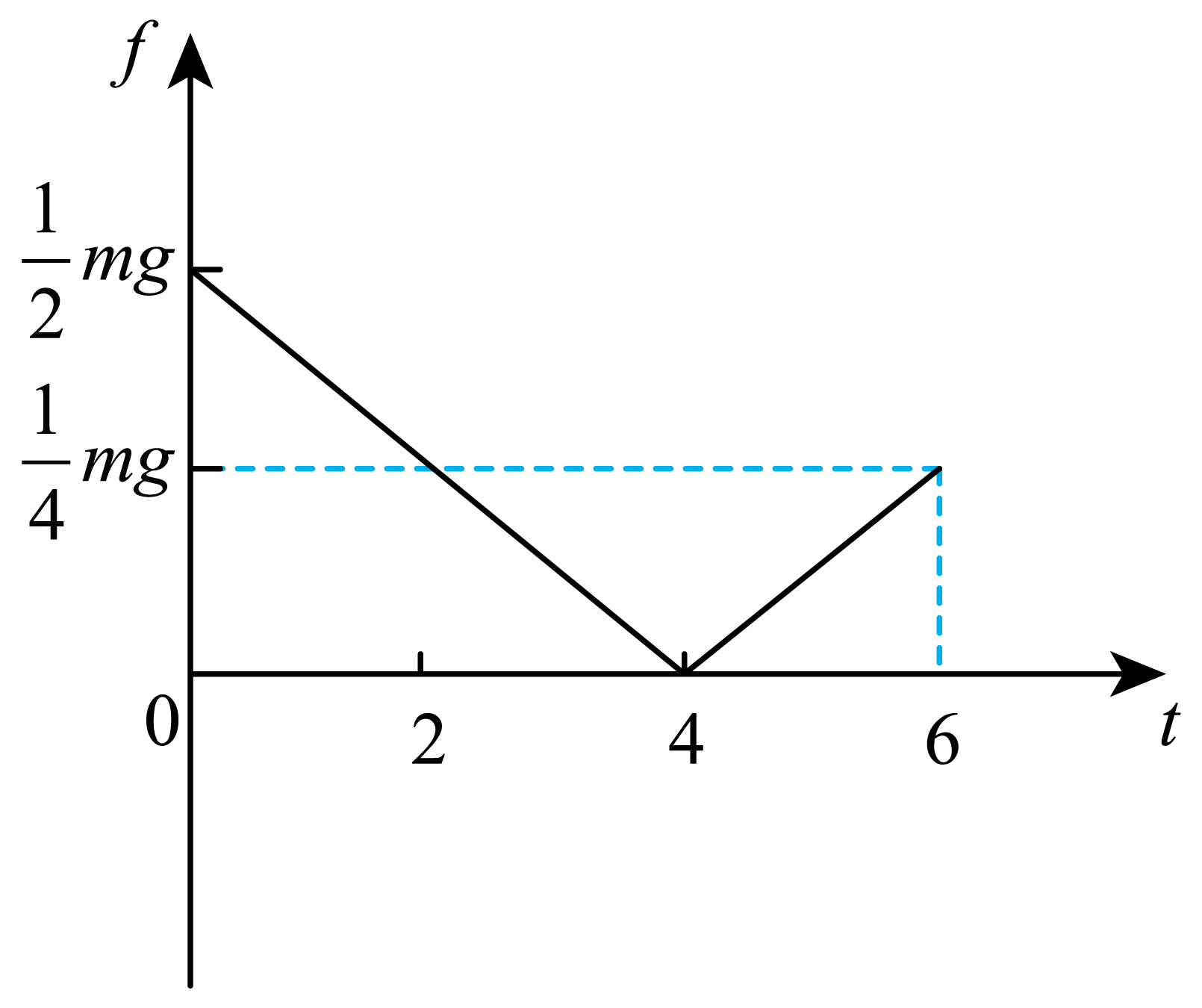
$t=6\;\rm s$时,物块的速度大小。
$v=\\dfrac{17}{2}g$
"]]在$0$~$6\;\rm s$内沿杆方向根据动量定理有$I_{F}\cos \theta − I_{f}+mg\sin \theta \times t=mv$
在$0$~$6\;\rm s$内摩擦力的冲量为$f$−$t$图围成的面积,则$I_{\text{f}}=\dfrac{1}{2} \times \dfrac{1}{2}mg \times 4+\dfrac{1}{2} \times \dfrac{1}{4}mg \times 2=\dfrac{5}{4}mg$
联立有$\dfrac{9\sqrt{3}}{2}mg \cdot \cos 30^{^\circ}+3mg-\dfrac{5}{4}mg=mv$
可得$v=\dfrac{17}{2}g$
高中 | 牛顿第二定律的两类基本问题题目答案及解析(完整版)
