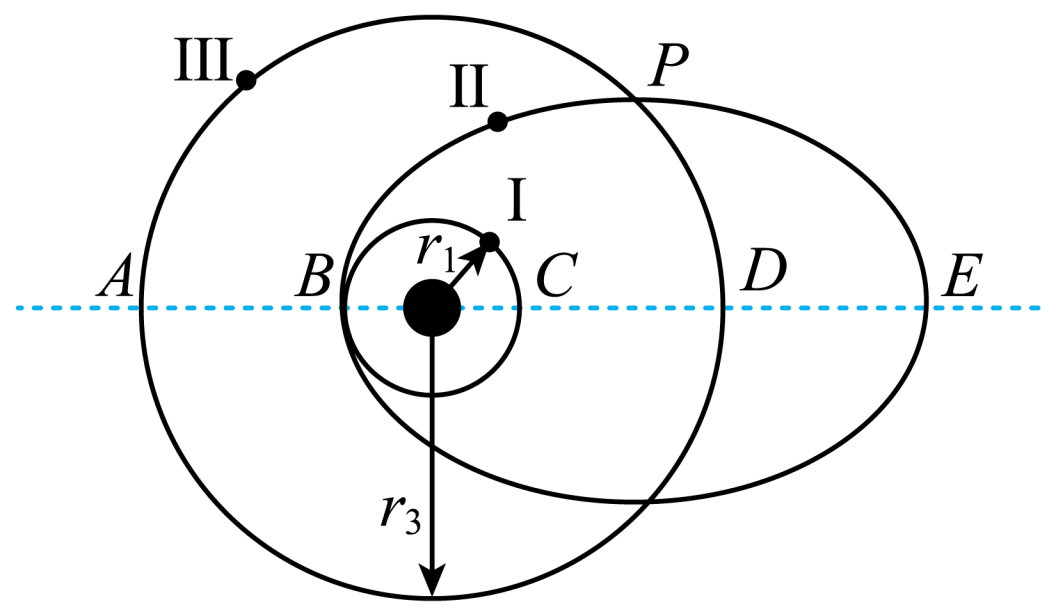
宇宙中有一孤立星系，中心天体的周围有三颗行星，如图所示。中心天体质量远大于行星质量，不考虑行星之间的万有引力，行星$\rm I$、$\rm III$运行的圆轨道半径分别为$r_{1}$、$r_{3}$，行星$\rm II$运行的椭圆轨道半长轴$a=r_{3}$，且与行星$\rm I$轨道在$B$点相切，行星$\rm II$轨道距中心天体最远处为$E$，则行星$\rm II$、$\rm III$的运行周期之比为                 ，行星$\rm I$、$\rm II$在$B$点的加速度之比为                 ，行星$\rm II$在$B$、$E$两点的速率之比为                 。

根据开普勒第三定律可得$\dfrac{a^{3}}{T_{2}^{2}}=\dfrac{r_{3}^{3}}{T_{3}^{2}}$，可得$T_{2}:T_{3}=1:1$

根据牛顿第二定律$G\dfrac{Mm}{r^{\text{2}}}=ma$，解得$a=G\dfrac{M}{r^{\text{2}}}$

又因为行星$I$、$II$在$B$点时到中心天体的距离相等，所以$a_{1}:a_{2}=1:1$

分别在$B$、$E$两点附近取很小的一段相等的时间$\Delta t$，则行星与中心天体在$\Delta t$连线扫过的面积近似可看成扇形，根据开普勒第二定律有$\dfrac{1}{2}r_{B}v_{B}\Delta t=\dfrac{1}{2}r_{E}v_{E}\Delta t$，解得$\dfrac{v_{B}}{v_{E}}=\dfrac{r_{E}}{r_{B}}=\dfrac{2r_{3}-r_{1}}{r_{1}}$