北斗卫星导航系统采用了混合轨道部署模式，三十多颗北斗卫星的圆轨道拥有共同的圆心，卫星做圆周运动的向心力由                 力提供。

由题可知，卫星圆周运动的向心力由地球对卫星的万有引力提供；

如图所示为在同一轨道平面上的三颗不同的人造地球卫星，关于各物理量的关系，下列说法正确的是$(\qquad)$

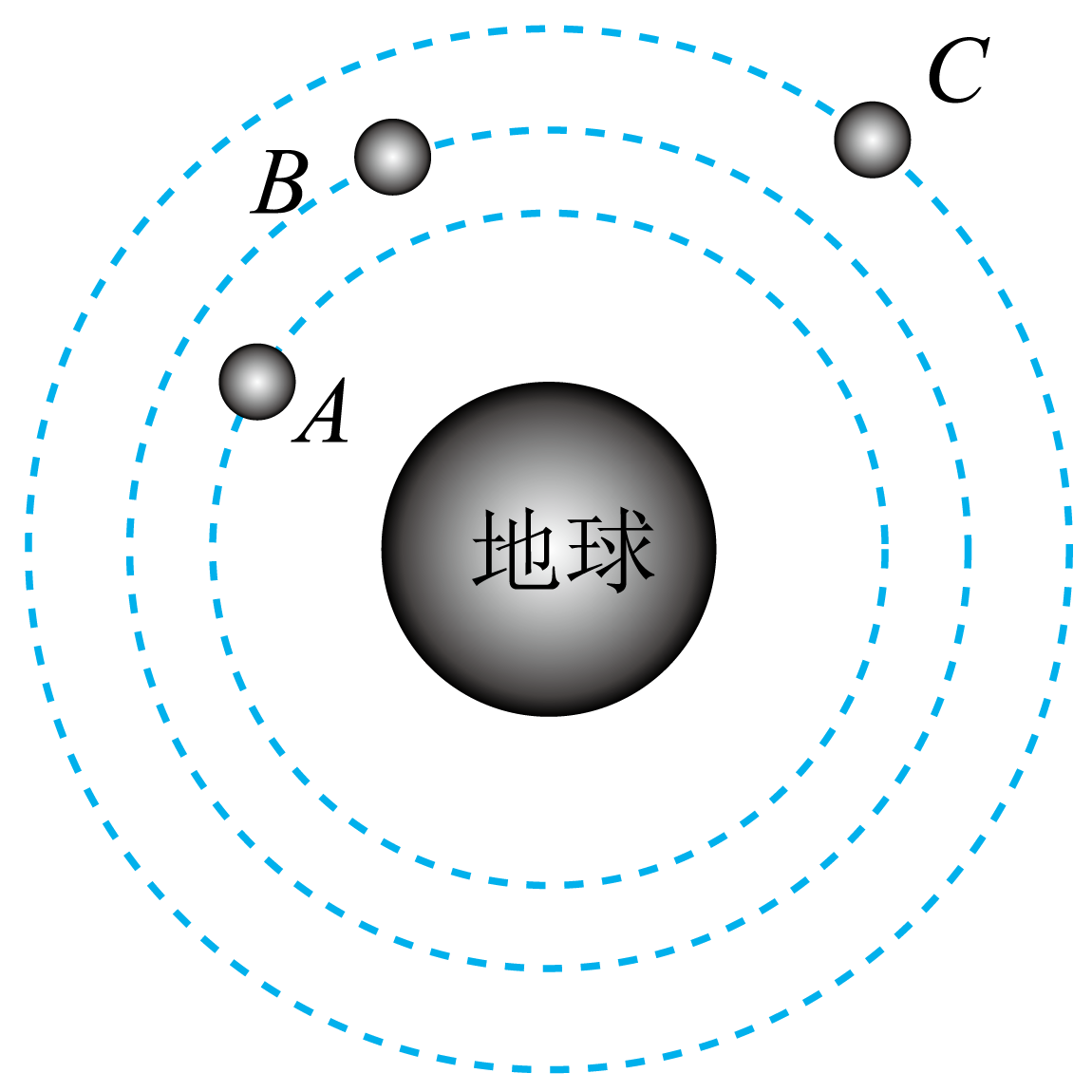
三颗卫星的线速度$v_{A}\\gt v_{B}\\gt v_{C}$

根据万有引力定律，可知三颗卫星所受地球引力$F_{A}\\gt F_{B}\\gt F_{C}$

三颗卫星的周期$T_{A}\\gt T_{B}\\gt T_{C}$

三颗卫星的向心加速度$a_{A}\\lt a_{B}\\lt a_{C}$

$\rm A$．根据万有引力提供向心力则有$\dfrac{GMm}{r^{2}}= \dfrac{mv^{2}}{r}$，解得$v= \sqrt{\dfrac{GM}{r}}$，由于三颗卫星的轨道半径$r_{A}\lt r_{B}\lt r_{C}$，因此三颗卫星的线速度大小关系为$v_{A}\gt v_{B}\gt v_{C}$，故$\rm A$正确；

$\rm B$．根据万有引力定律$F=\dfrac{GMm}{r^{2}}$可知，由于三颗卫星的质量$m$未知，故无法比较卫星受到地球对其万有引力的大小，故$\rm B$错误；

$\rm C$．根据万有引力定律可得$\dfrac{GMm}{r^{2}}=m{\left(\dfrac{2\pi}{T}\right)}^{2}r$，解得$T=2\pi\sqrt{\dfrac{r^{3}}{GM}}$，由于三颗卫星的轨道半径$r_{A}\lt r_{B}\lt r_{C}$，因此三颗卫星的周期$T_{A}\lt T_{B}\lt T_{C}$，故$\rm C$错误；

$\rm D$．根据万有引力定律可得$\dfrac{GMm}{r^{2}}=ma$，解得$a=\dfrac{GM}{r^{2}}$，由于三颗卫星的轨道半径$r_{A}\lt _{B}\lt r_{C}$，因此三颗卫星的加速度$a_{A}\gt a_{B}\gt a_{C}$，故$\rm D$错误。

故选：$\rm A$。

$2023$年$5$月$30$日，“神舟十六号”载人飞船发射成功，将航天员送入空间站，他们执行任务时通过同步卫星与地面实时联系。已知空间站运行周期约为$90\;\rm \min$，它与同步卫星的运行轨道均视为圆周轨道，则$(\qquad)$

空间站相对地面静止

空间站的速度大于同步卫星的速度

空间站的速度大于第一宇宙速度

空间站的加速度小于同步卫星的加速度

$\rm A$．以地面为参考系，空间站是运动的，故$\rm A$错误；

$\rm B$．根据万有引力定律可得$\dfrac{GMm}{r^{2}}=m{\left(\dfrac{2\pi}{T}\right)}^{2}r$，解得$T=2\pi\sqrt{\dfrac{r^{3}}{GM}}$，可知$T \propto \sqrt{r^{3}}$，由题可知，空间站的周期小于地球同步卫星的周期，故空间站的轨道半径小于同步卫星的轨道半径，根据$\dfrac{GMm}{r^{2}}=\dfrac{mv^{2}}{r}$，可得$v=\sqrt{\dfrac{GM}{r}}$，因此空间站的速度大于同步卫星的速度，故$\rm B$正确；

$\rm C$．第一宇宙速度是最大的环绕速度，所以空间站的速度小于第一宇宙速度，故$\rm C$错误；

$\rm D$．结合上述分析可知，空间站的轨道半径小于同步卫星的轨道半径，由于万有引力提供向心力，根据牛顿第二定律可得$\dfrac{GMm}{r^{2}}=ma$，解得$a=\dfrac{GM}{r^{2}}$，因此空间站的加速度大于同步卫星的加速度，故$\rm D$错误。

故选：$\rm B$。

预计我国将在$2030$年前后实施航天员登月计划，航天员乘飞船登月后将进行一系列科学探测与实验。假如到达月球前航天员将乘飞船沿半径为$r$的轨道绕月做匀速圆周运动。登月后航天员在月球表面用测力计测得质量为$m_{0}$的物块重力为$G_{0}$。已知月球的半径为$R$，求：

①月球的质量。

②航天员乘飞船绕月运行一周所用的时间（写出计算过程）

①$\\dfrac{G_{0}R^{2}}{Gm_{0}}$；②$\\dfrac{2\\pi}{R}\\sqrt{\\dfrac{m_{0}r^{3}}{G_{0}}}$

①设月球的质量为$M$，根据牛顿第二定律可得$\dfrac{GMm_{0}}{R^{2}}=G_{0}$，解得$M=\dfrac{G_{0}R^{2}}{Gm_{0}}$

②根据牛顿第二定律可得$\dfrac{GMm_{0}}{r^{2}}=m_{0}{\left(\dfrac{2\pi}{T}\right)}^{2}r$，解得$T=2\pi\sqrt{\dfrac{r^{3}}{GM}}$

结合上述结论$GM=\dfrac{G_{0}R^{2}}{m_{0}}$，解得$T=\dfrac{2\pi}{R}\sqrt{\dfrac{m_{0}r^{3}}{G_{0}}}$