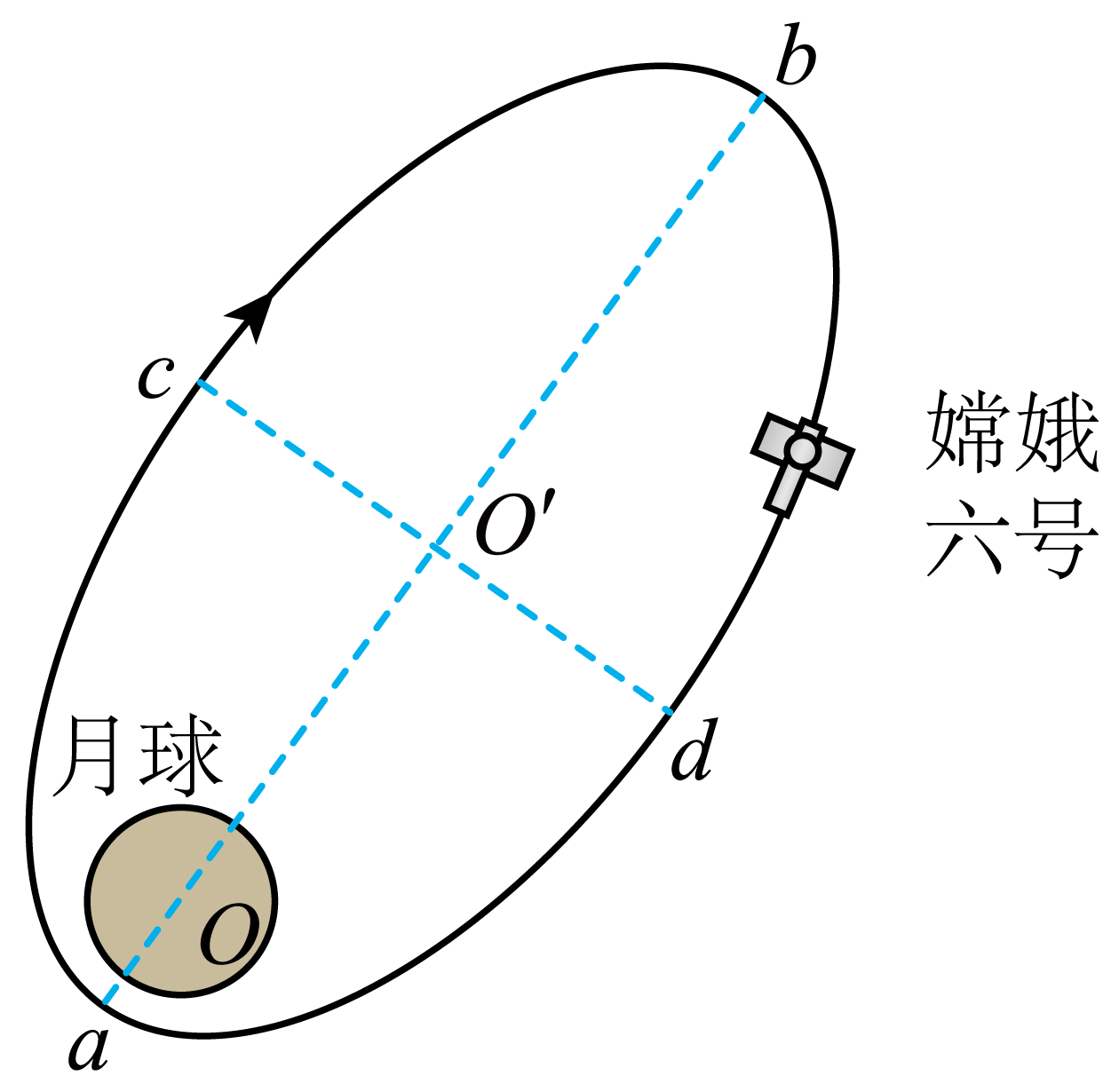
如图，嫦娥六号在环月椭圆轨道上沿图中箭头方向运动，仅考虑月球对它的引力，$ab$为椭圆轨道长轴，$cd$为椭圆轨道短轴。嫦娥六号从$a$点运动到$b$点的过程中，动能$(\qquad)$

增大

先增大后减小

减小

先减小后增大

根据开普勒第二定律可知，相同时间内嫦娥六号与月球连线扫过的面积相等，又因为嫦娥六号从$a$点运动到$b$点的过程中，嫦娥六号与月球连线变大，所以速率减小，动能减小；

故选：$\rm C$；

嫦娥探测器从椭圆环月轨道变轨为圆形环月轨道，圆形环月轨道对应的周期为$T$，离月球表面高度为$h$。已知月球半径为$R$，万有引力常量为$G$。

①求月球的质量$M$                ；

②求月球表面的重力加速度大小$g_{月}$                ；

③假设未来的你是宇航员，登陆月球后，要测量月球表面的重力加速度，请简要写出一种测量方案                。

$\\dfrac{4\\pi^{2}{(R+ h)}^{3}}{GT^{2}}$; $\\dfrac{4\\pi^{2}{(R+ h)}^{3}}{T^{2}R^{2}}$ ;见解析

设嫦娥六号的质量为$m$，根据万有引力提供向心力$G\dfrac{Mm}{{(R+h)}^{2}}= m\dfrac{4\pi^{2}}{T^{2}}(R+h)$，解得月球的质量为$M=\dfrac{4\pi^{2}{(R+ h)}^{3}}{GT^{2}}$

设月球表面上一个物体的质量为$m'$，则$G\dfrac{Mm'}{R^{2}}=m'g_{月}$，解得月球表面的重力加速度大小$g_{月}=\dfrac{4\pi^{2}{(R+h)}^{3}}{T^{2}R^{2}}$

用弹簧测力计测出一个质量为$m$的钩码的重力$G$，则月球表面的重力加速度$g=\dfrac{G}{m}$，在距月球表面高$h$处，由静止释放一个小钢球，测出其运动时间$t$，则月球表面的重力加速度$g=\dfrac{2h}{t^{2}}$，或在月球表面某一高度释放手机，利用手机内的加速度传感器测月球表面的重力加速度。