小明在学习完圆周运动知识后对修正带的内部结构进行研究。如图，修正带盘固定在大齿轮的转轴上大、小齿轮相互咬合，齿数之比为$2:1$。图中$a$、$b$点分别位于大、小齿轮的边缘，$c$点位于大齿轮的转轴半径中点。当修正带被匀速拉动进行字迹修改时，$a$、$b$点的角速度大小之比为                 ，$b$、$c$点的向心加速度大小之比为                 。

由题可知，$a$、$b$两点的线速度相等，则有$v_{a}=v_{b}$，$v=\omega r$，联立可得$\omega_{a}:\omega_{b}=r_{b}:r_{a}=1:2$

由题可知$\omega_{c}=\omega_{a}$，$r_{c}=r_{b}$，根据$a_{n}=\omega^{2}r$，可得$b$、$c$点的向心加速度大小之比为$a_{b}:a_{c}=\omega_{b}^{2}r_{b}:\omega_{c}^{2}r_{c}=\omega_{b}^{2}:\omega_{c}^{2}=\omega_{b}^{2}:\omega_{a}^{2}=4:1$

在铁路转弯处，外轨往往略高于内轨，火车在某个弯道按规定的运行速度转弯时，内、外轨对车轮皆无侧压力。火车提速后在该弯道运行时，下列说法正确的是$(\qquad)$

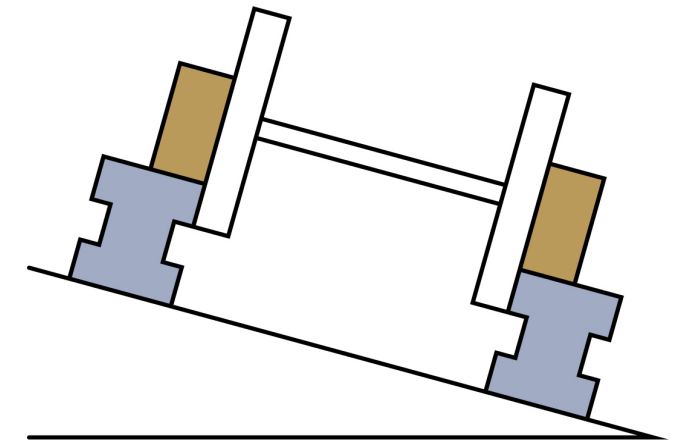
内轨对车轮的轮缘有侧压力

外轨对车轮的轮缘有侧压力

内、外轨对车轮的轮缘都有侧压力

内、外轨对车轮的轮缘均无侧压力

火车提速后，火车转弯的速度大于规定的速度，火车有做离心运动的趋势，重力和支持力的合力小于火车需要的向心力，此时外轨对轮缘有侧压力。

故选：$\rm B$。

为探究向心力大小与半径、角速度、质量的关系，小明按如图装置进行实验，物块放在平台卡槽内，平台绕轴转动，物块做匀速圆周运动，平台转速可以控制，光电计时器可以记录转动一周的时间。

①为了探究向心力与角速度的关系，需要控制                 保持不变，小明由计时器测转动的周期$T$，计算$\omega^{2}$的表达式是                 。

②小明按上述实验将测算得的结果用作图法来处理数据，如图所示纵轴$F$为力传感器读数，横轴为$\omega^{2}$，图线不过坐标原点的原因是                 ，用电子天平测得物块质量为$1.50\;\rm kg$，直尺测得半径为$50.00\;\rm cm$，图线斜率大小为                 （结果保留两位有效数字）。

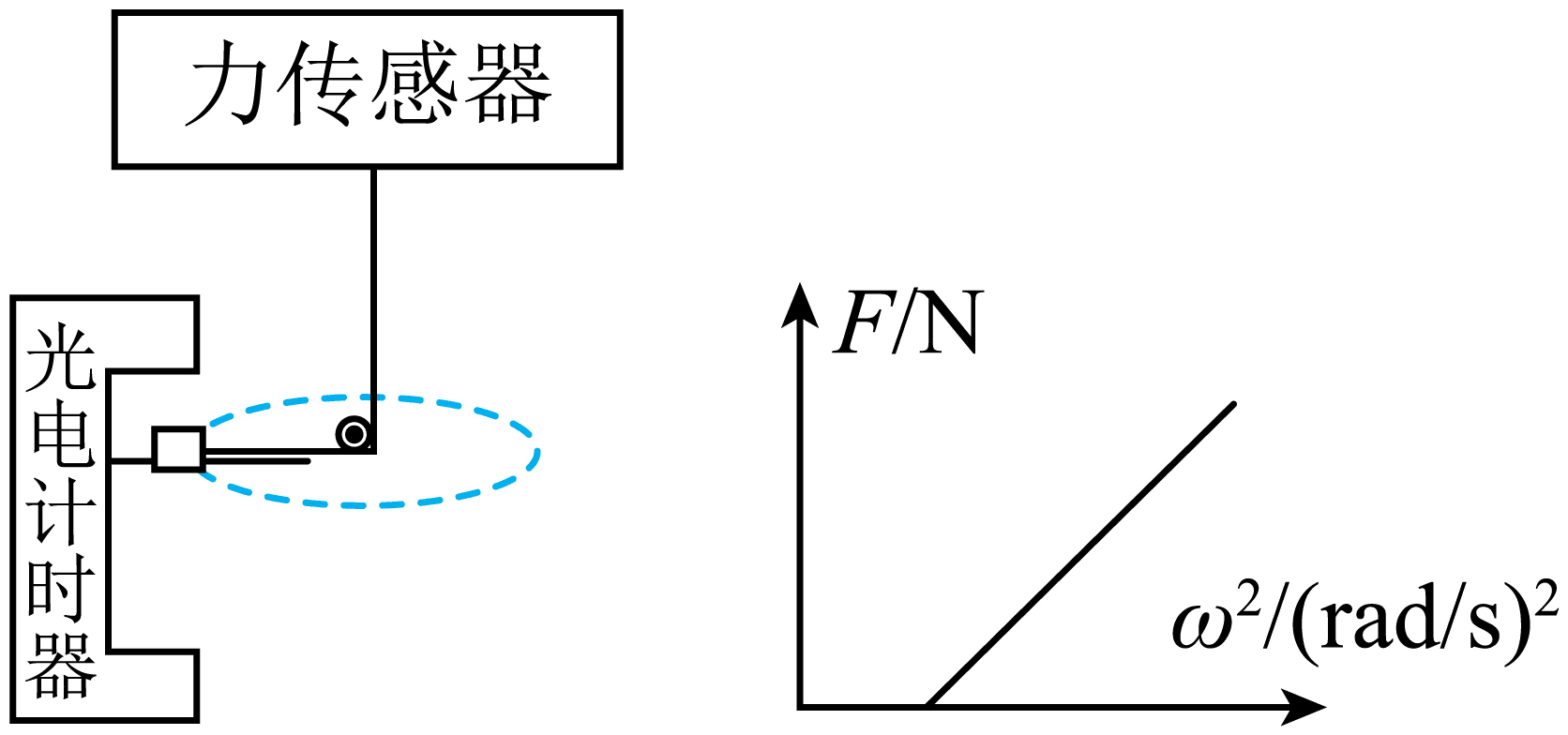
①根据控制变量法可知，要探究向心力与角速度的关系，需控制小球的质量和轨道半径不变，只改变小球的角速度即可；

根据$T=\dfrac{2\pi}{\omega}$，可得$\omega^{2}=\dfrac{4\pi^{2}}{T^{2}}$

②对物体受力分析，结合牛顿第二定律可得$F+f=m\omega^{2}r$，解得$F=m\omega^{2}r-f$，故在$F-\omega^{2}$图像中，其纵截距表示物体受到的摩擦力的大小，故图像不过原点是由于物体受到摩擦力的影响；

结合上述分析可知，$F-\omega^{2}$图线的斜率为$k=mr=1.50 \times 0.5\;\rm kg ⋅ m=0.75\;\rm kg ⋅ m$

图甲为游乐园中“空中飞椅”的游戏设施。若将人和座椅看成一个质点，则可简化为如图乙所示的物理模型，其中$P$为处于水平面内的转盘，可绕竖直转轴$OO'$转动，$O$点距地面高度为$18\;\rm m$，设绳长$L=10\;\rm m$，质点的质量$m=60\;\rm kg$，转盘静止时质点与转轴之间的距离$d=4.0\;\rm m$，转盘逐渐加速转动，经过一段时间后质点与转盘一起做匀速圆周运动，此时绳与竖直方向的夹角$\theta=37^\circ $，不计空气阻力及绳重，且绳不可伸长，$\sin37^\circ =0.6$，$\cos37^\circ =0.8$，$g=10\;\rm m/s^{2}$，求质点与转盘一起做匀速圆周运动时（写出计算过程）：

①绳子拉力的大小；

②转盘角速度的大小；

①$750\\;\\rm N$；②$\\dfrac{\\sqrt{3}}{2}\\ \\text{rad/s}$

对人和座椅受力分析，如图所示

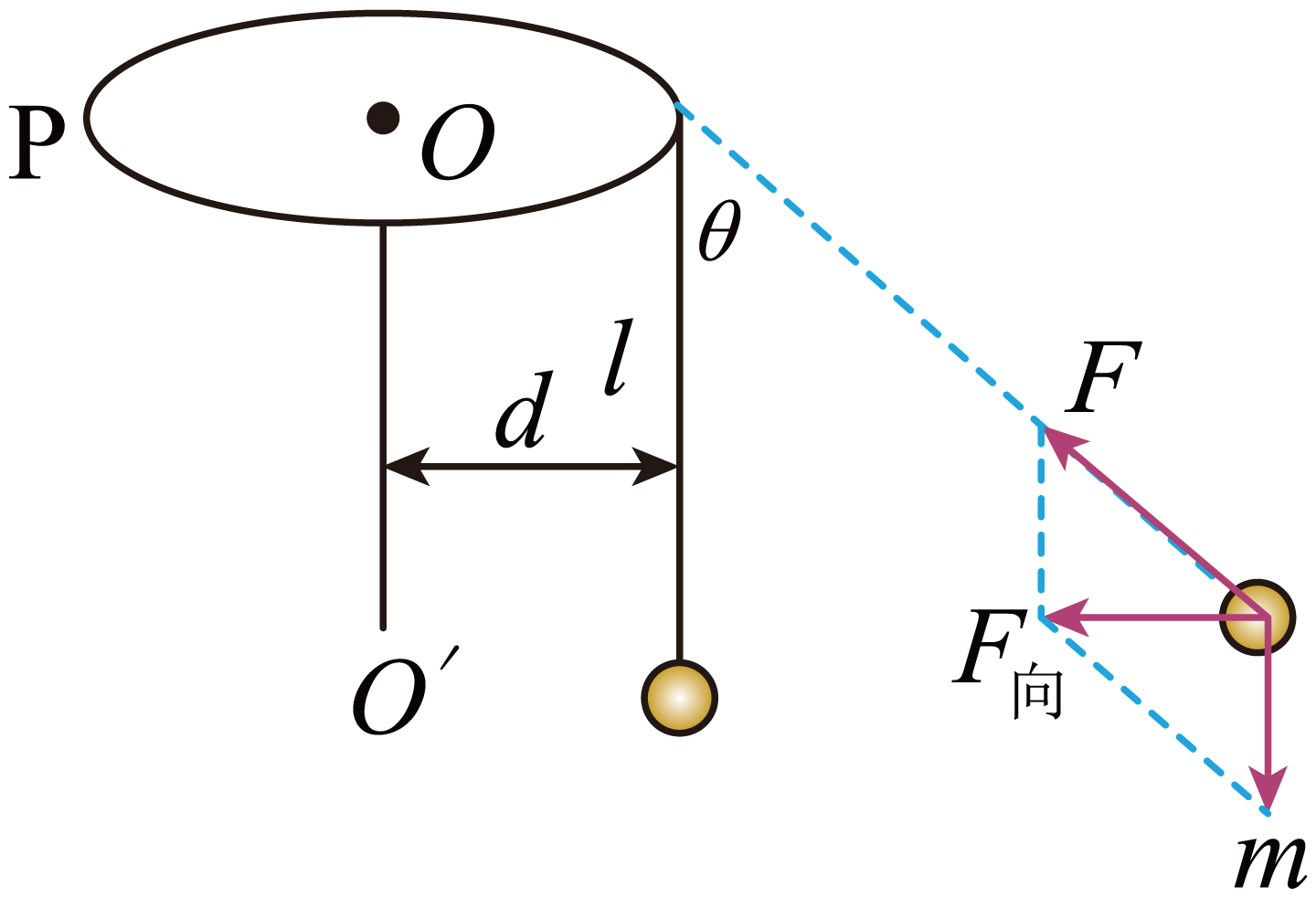
在竖直方向上，由平衡条件可得$F\cos 37^\circ =mg$

水平方向上，根据牛顿第二定律可得$mg\tan 37^\circ =m\omega^{2}(d+l\sin 37^\circ )$

联立解得$F=750\;\rm N$，$\omega=\dfrac{\sqrt{3}}{2}\ \text{rad/s}$