如图所示为生活中常见的四种圆周运动，下列说法正确的是$(\qquad)$

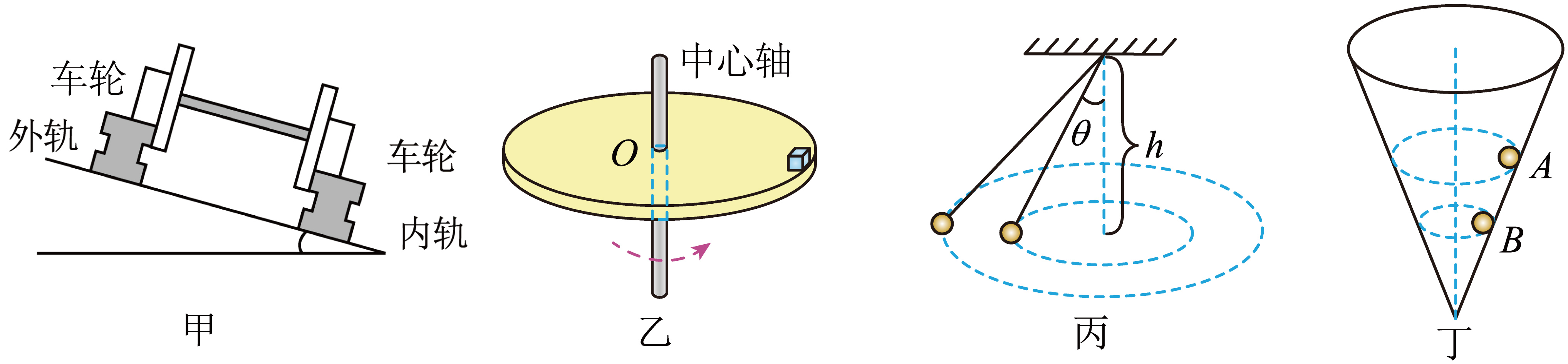
图甲中，火车转弯超过规定速度行驶时，内轨对轮缘会有挤压作用

图乙中，与水平圆盘一起匀速转动的物块，角速度越大，物块受到的静摩擦力越大

图丙是圆锥摆，两个小球在同一水平面内做匀速圆周运动。$\\theta$角小的小球，圆周运动的角速度更大

图丁中，光滑且竖直固定的圆锥筒内，一个小球先后分别在$A$、$B$两位置做匀速圆周运动。在$A$、$B$两位置小球的角速度大小不同，但所受筒壁的支持力大小相等

$\rm A$．图甲中，火车转弯超过规定速度行驶时，火车有离心运动趋势，外轨对轮缘会有挤压作用，故$\rm A$错误；

$\rm B$．图乙中，与水平圆盘一起匀速转动的物块，根据牛顿第二定律可得$f_{静}=m\omega^{2}r$

可知角速度越大，物块受到的静摩擦力越大，故$\rm B$正确；

$\rm C$．以小球为对象，根据牛顿第二定律可得$mg\tan \theta=m\omega^{2}r=m\omega^{2}\;\rm h\tan \theta$

可得角速度为$\omega=\sqrt{\dfrac{g}{h}}$

可知图丙中两小球的角速度相等，故$\rm C$错误；

$\rm D$．设圆锥筒母线与竖直方向的夹角为$\theta$，以小球为对象，竖直方向根据受力平衡可得$N\sin \theta=mg$

可得小球所受筒壁的支持力大小为$N=\dfrac{mg}{\sin\theta}$

以小球为对象，水平方向根据牛顿第二定律可得$F_{合}=\dfrac{mg}{\tan\theta}=m\omega^{2}r$

可得角速度为$\omega=\sqrt{\dfrac{g}{r\tan\theta}}$

则一个小球先后分别在$A$、$B$两位置做匀速圆周运动，由于$\theta$不变，$r$不同，所以在$A$、$B$两位置小球的角速度大小不同，但所受筒壁的支持力大小相等，故$\rm D$正确。

故选：$\rm BD$。