为避免火车在水平面上过弯时因内外轨道半径不同致使轮子打滑造成危险（不考虑离心问题），把固定连接为一体的两轮设计成锥顶角$\theta$很小的圆台形，如图所示。设铁轨间距为$L$，正常直线行驶时两轮与铁轨接触处的直径均为$D$，过弯时内外轨间中点位置到轨道圆心的距离为过弯半径$R$。在$\theta$很小时，$\tan\theta ≈ \sin\theta ≈ \theta$。若在水平轨道过弯时要求轮子不打滑且横向偏移量不超过$\Delta x$，则最小过弯半径$R$为$(\qquad)$

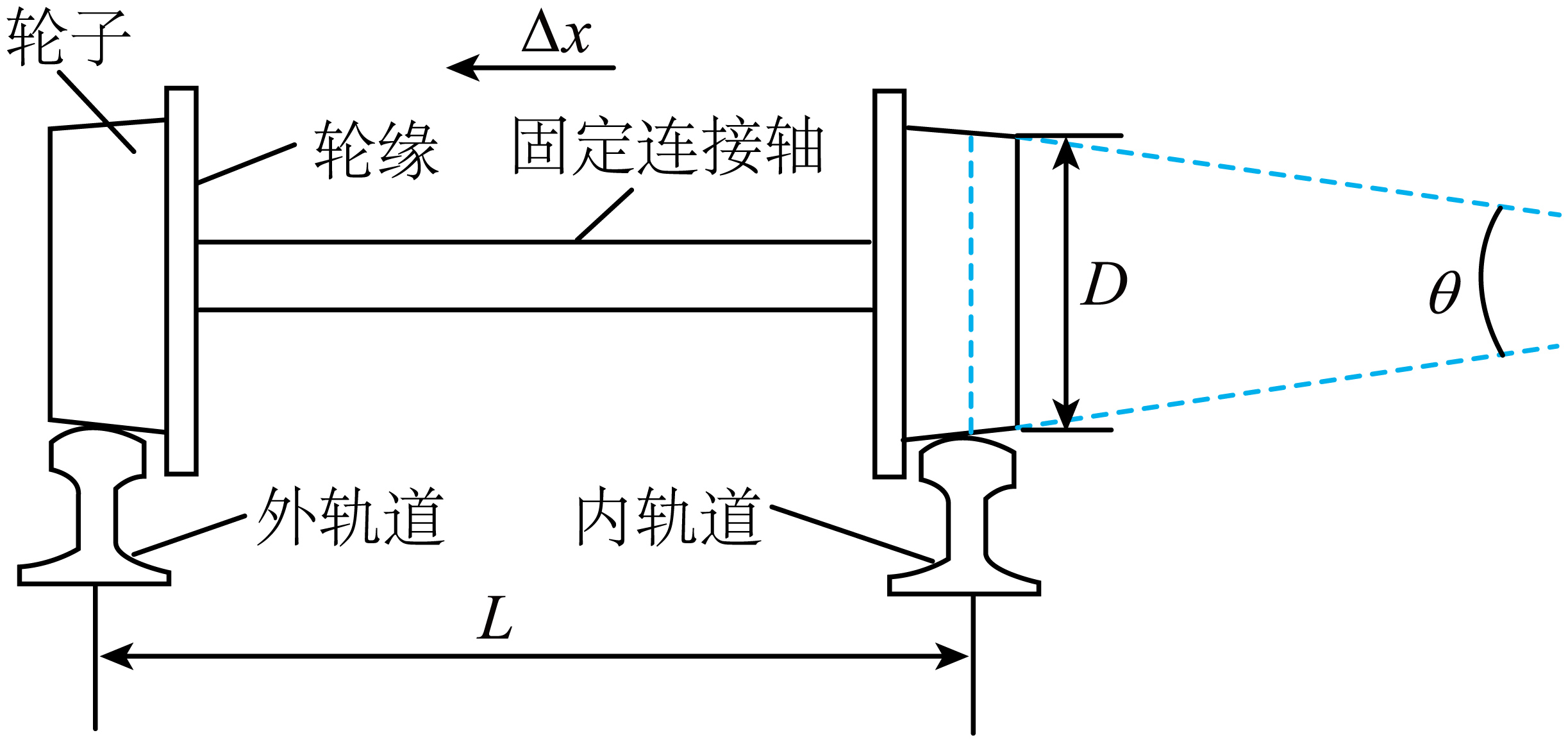
$\\dfrac{2LD}{\\theta\\Delta x}$

$\\dfrac{LD}{\\theta\\Delta x}$

$\\dfrac{LD}{2\\theta\\Delta x}$

$\\dfrac{LD}{4\\theta\\Delta x}$

根据题意可知，转弯时车轮会向外偏移$\Delta x$，这样导致轮子与外铁轨接触的位置半径增大为$r_{1}$，根据几何关系有$2r_{1}=D+2\Delta x\tan\dfrac{\theta}{2}$

同理可知，轮子与内铁轨接触的位置半径减小为$r_{2}$，则有$2r_{2}=D-2\Delta x\tan\dfrac{\theta}{2}$

设一段时间内，外轨道轮子与铁轨接触的位置向前运动的距离为$s_{1}$，内轨道轮子与铁轨接触的位置向前运动的距离为$s_{2}$，由于两轮固定连接为一体，且轮子不打滑，则有$\dfrac{s_{1}}{s_{2}}=\dfrac{r_{1}}{r_{2}}=\dfrac{D+2\Delta x\tan\dfrac{\theta}{2}}{D-2\Delta x\tan\dfrac{\theta}{2}}$

由于$\tan\dfrac{\theta}{2} \approx \dfrac{\theta}{2}$

则有$\dfrac{s_{1}}{s_{2}}=\dfrac{D+\theta\Delta x}{D-\theta\Delta x}$

转弯过程俯视图，如图所示

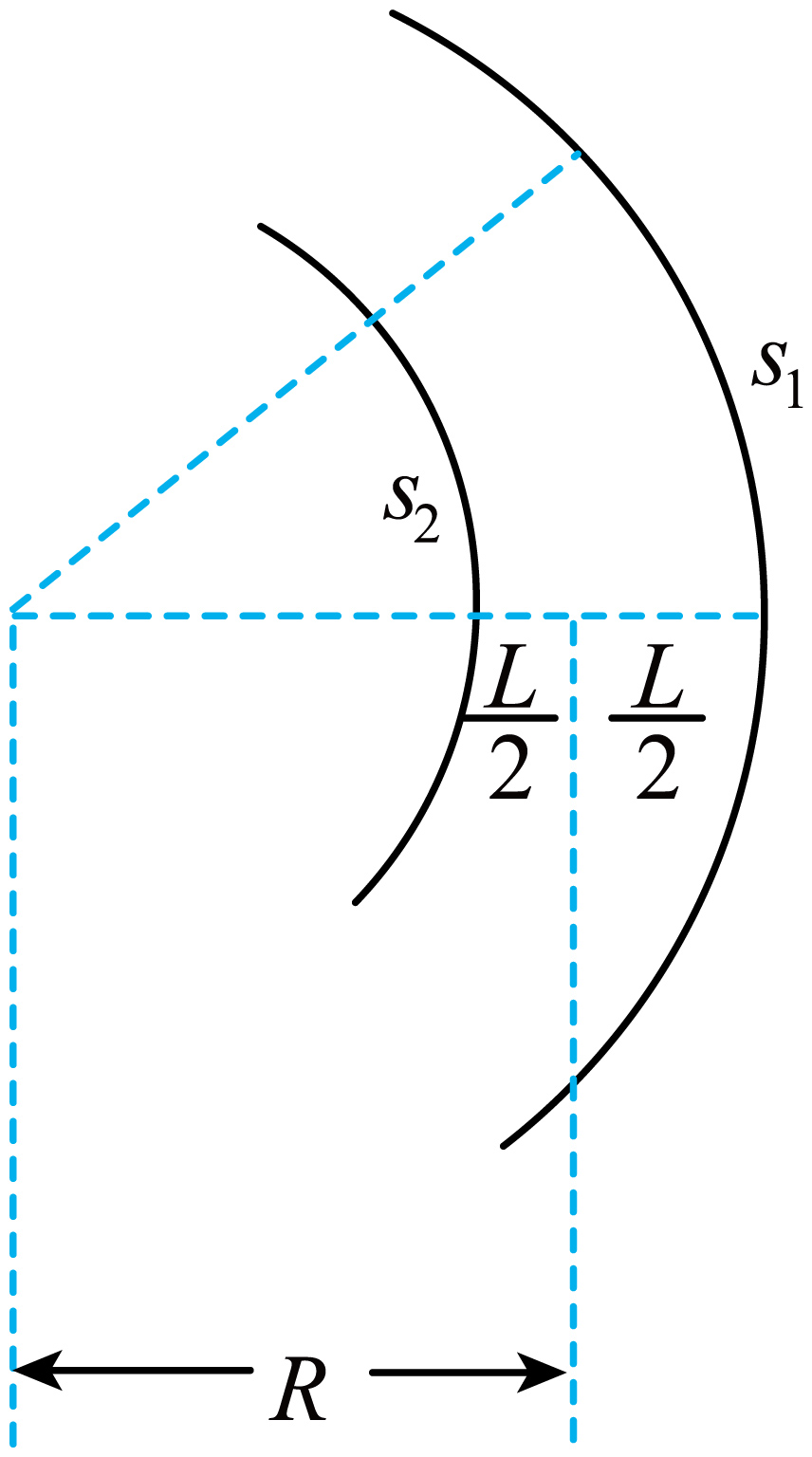
由几何关系有$\dfrac{s_{1}}{s_{2}}=\dfrac{R+\dfrac{L}{2}}{R-\dfrac{L}{2}}$

联立解得$R=\dfrac{LD}{2\theta\Delta x}$

故选：$\rm C$。