$2025$年$5$月$1$日，全球首个实现“聚变能发电演示”的紧凑型全超导托卡马克核聚变实验装置（$BEST$）在我国正式启动总装。如图是托卡马克环形容器中磁场截面的简化示意图，两个同心圆围成的环形区域内有垂直纸面向里的匀强磁场，磁感应强度大小为$B$，内圆半径为$R_{0}$。在内圆上$A$点有$a$、$b$、$c$三个粒子均在纸面内运动，并都恰好到达磁场外边界后返回。已知$a$、$b$、$c$带正电且比荷均为$\dfrac{q}{m}$，$a$粒子的速度大小为$v_{a}=\dfrac{qBR_{0}}{m}$，方向沿同心圆的径向；$b$和$c$粒子速度方向相反且与$a$粒子的速度方向垂直。不考虑带电粒子所受的重力和相互作用。下列说法正确的是$(\qquad)$

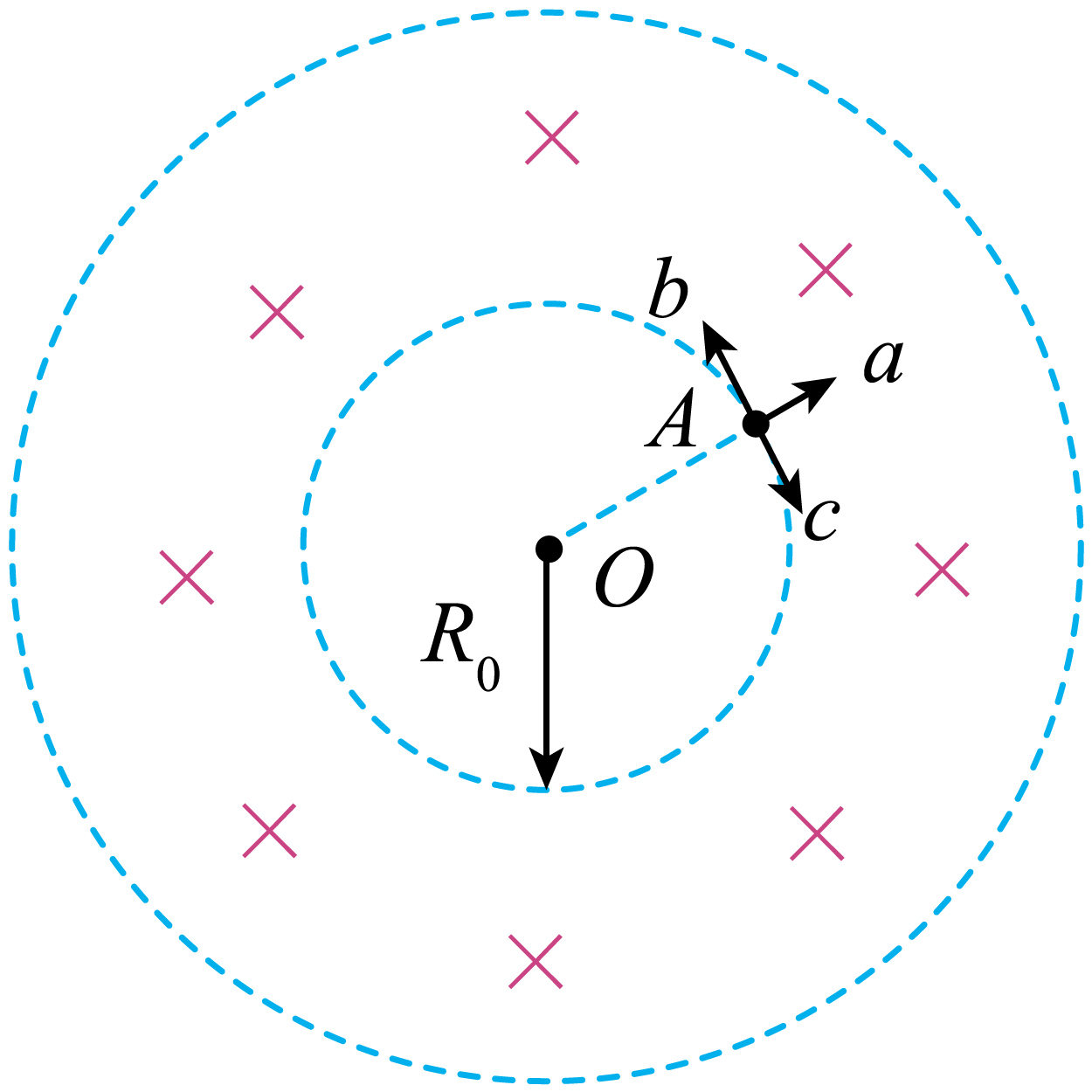
外圆半径等于$2R_{0}$

$a$粒子返回$A$点所用的最短时间为$\\dfrac{(3\\pi+2)m}{qB}$

$b$、$c$粒子返回$A$点所用的最短时间之比为$\\dfrac{\\sqrt{2}}{\\sqrt{2}+2}$

$c$粒子的速度大小为$\\dfrac{\\sqrt{2}}{2}v_{a}$

由题意，作出$a$粒子运动轨迹图，如图所示

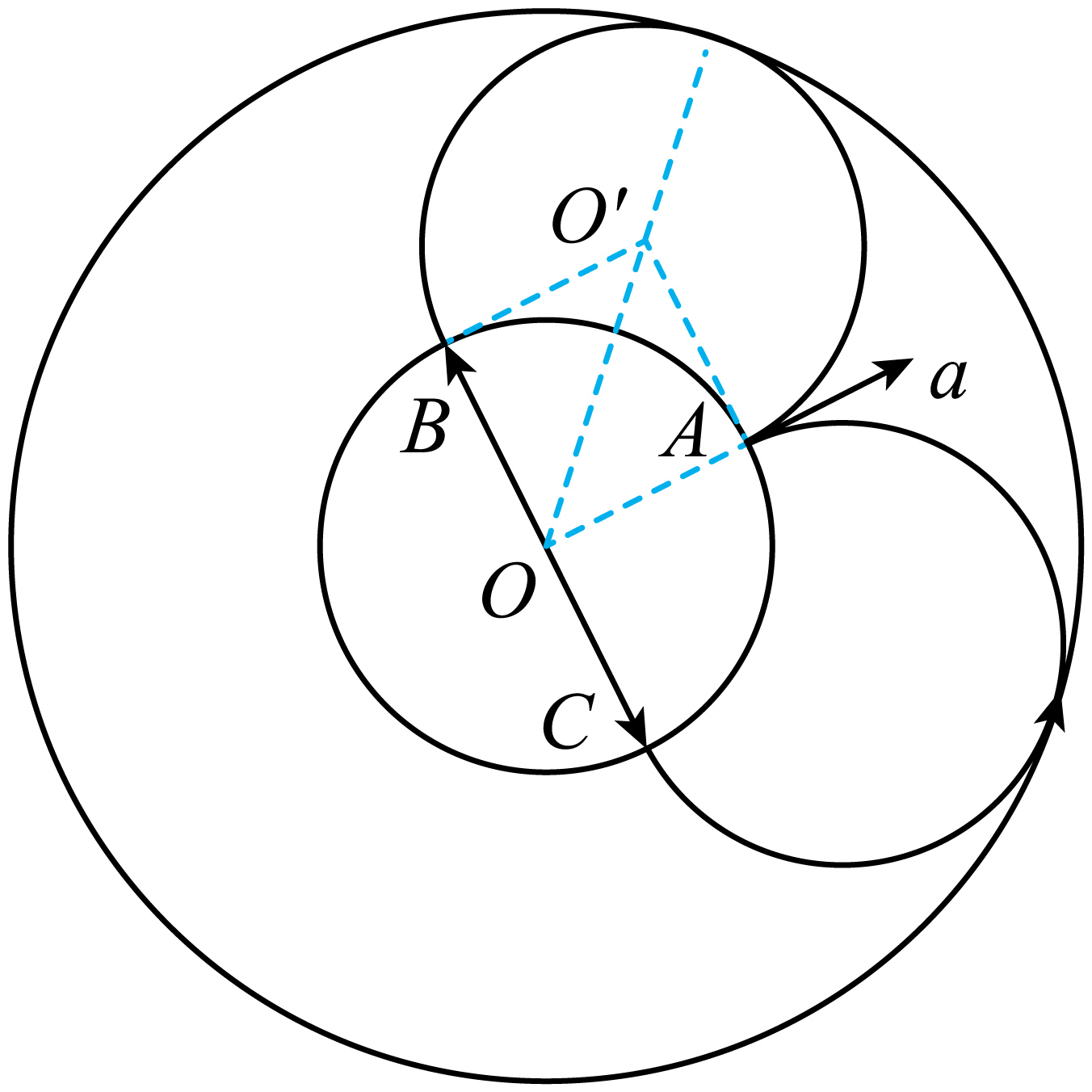
$a$粒子恰好到达磁场外边界后返回，$a$粒子运动的圆周正好与磁场外边界，然后沿径向做匀速直线运动，再做匀速圆周运动恰好回到$A$点，

根据$a$粒子的速度大小为$v_{a}=\dfrac{qBR_{0}}{m}$

可得$R_{a}=R_{0}$

设外圆半径等于$R^{^\prime}$,由几何关系得$∠AO'B=270^{\circ}$

则$R'=R_{0}+\sqrt{2}R_{0}$

$\rm A$错误；

$\rm B$．由$\rm A$项分析，$a$粒子返回$A$点所用的最短时间为第一次回到$A$点的时间$t_{\min}$

$a$粒子做匀速圆周运动的周期$T=\dfrac{2\pi R_{0}}{v_{a}}=\dfrac{2\pi m}{qB}$

在磁场中运动的时间$t_{1}=\dfrac{540{^\circ}}{360{^\circ}} \cdot T=\dfrac{3\pi m}{qB}$

匀速直线运动的时间$t_{2}=\dfrac{2R_{0}}{v_{a}}=\dfrac{2m}{qB}$

故$a$粒子返回$A$点所用的最短时间为$t_{\min}=t_{1}+t_{2}=\dfrac{(3\pi+2)m}{qB}$

$\rm B$正确；

$\rm C$．由题意，作出$b、c$粒子运动轨迹图，如图所示

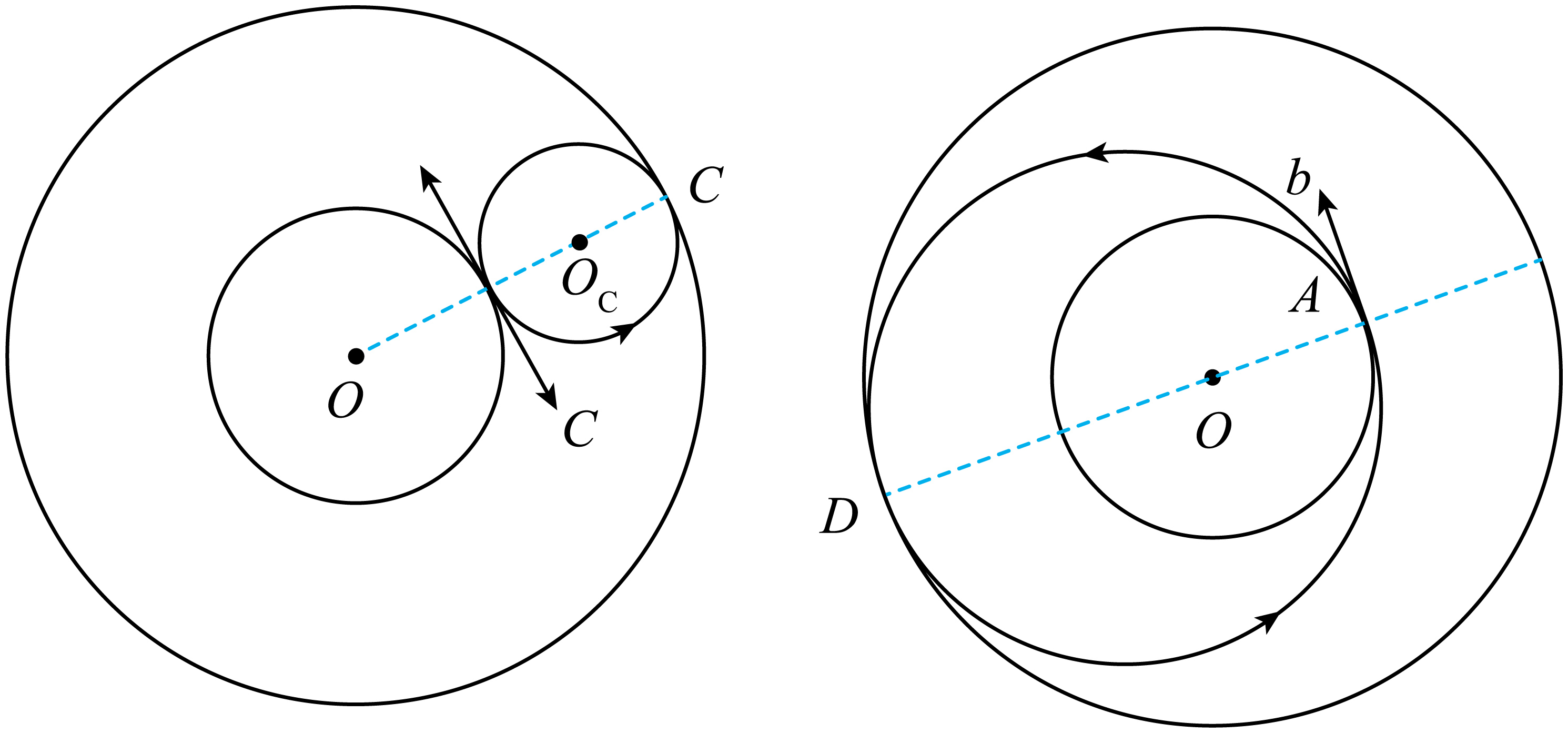
因为$b$、$c$粒子返回$A$点都是运动一个圆周，根据$b$、$c$带正电且比荷均为$\dfrac{q}{m}$，所以两粒子做圆周运动周期相同，故所用的最短时间之比为$1:1$，$\rm C$错误；

$\rm D$．由几何关系得$2R_{c}=\sqrt{2}R_{0}$

洛伦兹力提供向心力有$qv_{c}B=\dfrac{mv_{c}^{2}}{R_{c}}$

联立解得$v_{c}=\dfrac{\sqrt{2}}{2}v_{a}$

$\rm D$正确。

故选：$\rm BD$。