如图$1$所示，两波源$S_{1}$和$S_{2}$分别位于$x=-3\;\rm m$和$x=3\;\rm m$处，以$x=0$为边界，两侧为不同的均匀介质。$t=0$时刻，两波源同时向上振动，振幅均为$2\;\rm cm$，位于$x=1\;\rm m$处的质点$P$振动图像如图$2$所示，不考虑反射波带来的影响，以下说法正确的是$(\qquad)$

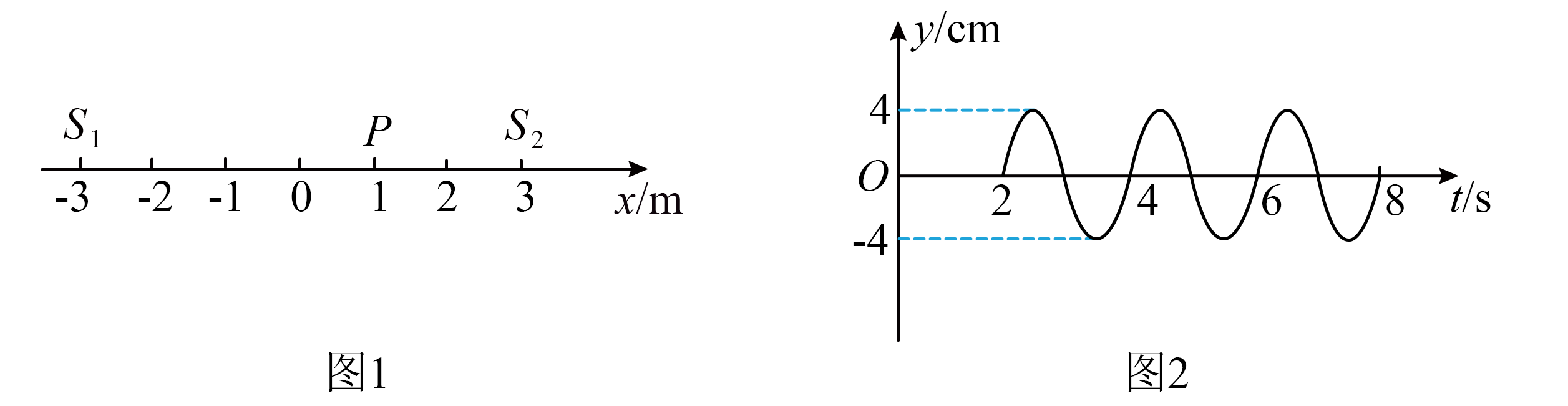
左侧介质中的波速为$3\\;\\rm m/s$

$t=5\\;\\rm s$时，$x=-1\\;\\rm m$处的质点位移为$-4\\;\\rm cm$

两波叠加稳定后，$S_{1}$、$S_{2}$之间（不包含$S_{1}$、$S_{2}$）有$3$个加强点

$0\\sim 5\\;\\rm s$内，位于$x=2\\;\\rm m$处的质点运动路程为$8\\;\\rm cm$

$\rm A$．由图$2$可知，$t=2\;\rm s$时质点$P$开始振动，因两侧介质不同，则波速不同，设左侧波的波速为$v_{左}$，右侧波的波速为$v_{右}$，由图$1$可知从波源$S_{1}$发出的波先到$x=0\;\rm m$处，再从$x=0\;\rm m$处传到$P$处，则传播时间满足$2\;\rm \text{s}=\dfrac{3}{v_{左}}+\dfrac{1}{v_{右}}$

从波源$S_{2}$发出的波到$P$处，则传播时间满足$2\;\text{s}=\dfrac{2}{v_{右}}$

联立解得$v_{左}=3\;\rm m/s$，$v_{右}=1\;\rm m/s$，故$\rm A$正确；

$\rm B$．由图$2$可知，振动周期$T=2\;\rm s$，角频率为$\omega=\dfrac{2\pi}{T}=\pi\ \text{rad}/\text{s}$，且两列波的起振动方向都沿$y$轴正方向；由图$1$可知，$x=-1\;\rm m$处的质点在左侧介质，$S_{1}$到该点的距离为$2\;\rm m$，则左侧波传到该点的时间为$t_{1}=\dfrac{2}{v_{左}}=\dfrac{2}{3}\text{s}$

振动方程为$y_{1}=2\sin\left\lbrack \pi\left( t-\dfrac{2}{3} \right) \right\rbrack\ \text{cm}$

$x=-1\;\rm m$处的质点在左侧介质，$S_{2}$到该点的距离为$4\;\rm m$，则右侧波传到该点的时间为$t_{2}=\dfrac{4}{v_{右}}=4\;\rm \text{s}$

振动方程为$y_{1}=2\sin [\pi(t-4)]\;\rm cm$

当$t=5\;\rm s$时$y_{1}=2\sin\left\lbrack \pi\left( 5-\dfrac{2}{3} \right) \right\rbrack\ \text{cm}=2\sin\left( \dfrac{13\pi}{3} \right)\ \text{cm}=2\sin\left( \dfrac{13\pi}{3} \right)\ \text{cm}=\sqrt{3}\;\rm \text{cm}$，$y_{2}=2\sin [\pi(5-4)]\;\rm cm=2\sin (\pi)\;\rm cm=0\;\rm cm$

故此时$x=-1\;\rm m$处质点的合位移为$y=y_{1}+y_{2}=\sqrt{3}\;\rm \text{cm}$，故$\rm B$错误；

$\rm C$．左侧波的波长为$\lambda_{左}=v_{左}T=3 \times 2\;\rm m=6\;\rm m$

右侧波的波长为$\lambda_{右}=v_{右}T=1 \times 2\;\rm m=2\;\rm m$

设某点到$S_{1}$的距离为$x$，则到$S_{2}$的距离为$6\;{\rm m}-x$

则路程差为$\Delta x=|2x-6\;\rm m|$

根据振动加强点的条件，当$\Delta x=|2x-6\;\rm m|=n\lambda_{右}=2n$时

可解得当$n=0$时有$x=3\;\rm m$，当$n=1$有$x=2\;\rm m$，当$n=2$有$x=1\;\rm m$，当$n=3$有$x=6\;\rm m$（不符合题意），故当两波叠加稳定后，$S_{1}$、$S_{2}$之间（不包含$S_{1}$、$S_{2}$）有$3$个加强点；

当$\Delta x=|2x-6\;{\rm m}|=n\lambda_{左}=6n$时

可解得当$n=0$时有$x=3\;\rm m$，当$n=1$有$x=6\;\rm m$（不符合题意），故当两波叠加稳定后，$S_{1}$、$S_{2}$之间（不包含$S_{1}$、$S_{2}$）只有$1$个加强点，综上可知，两波叠加稳定后，$S_{1}$、$S_{2}$之间（不包含$S_{1}$、$S_{2}$）有$3$个加强点，故$\rm C$正确；

$\rm D$．由图$2$可知，振动周期$T=2\;\rm s$，可知波的周期也为$T=2\;\rm s$；由图$1$可知，$x=2\;\rm m$处的质点位移右侧介质，$S_{2}$到该点的距离为$1\;\rm m$，则该波传到该处的时间为$t_{3}=\dfrac{1}{v_{右}}\ \text{s}=1\;\rm \text{s}$

振动时间为$\Delta t=5\;\rm s-1\;\rm s=4\;\rm s$

$S_{1}$到该点的距离为$5\;\rm m$，则该波传到该处的时间为$t_{4}=\dfrac{3}{v_{左}}\ \text{s}+\dfrac{2}{v_{右}}=3\;\rm \text{s}$

振动时间为$\Delta t'=5\;\rm s-3\;\rm s=2\;\rm s$

故在前$2\;\rm s$内（即一个周期内）只有波源$S_{2}$发出的波对$x=2\;\rm m$处质点的振动有影响；在后$2\;\rm s$内（即一个周期内）波源$S_{2}$发出的波和波源$S_{1}$发出的波，都对$x=2\;\rm m$处质点的振动有影响；又$\rm C$项可知$x=2\;\rm m$处是振动加强点，所以在后$2\;\rm s$内的两波叠加后振幅为$4\;\rm cm$，故在$0\sim 5\;\rm s$内，位于$x=2\;\rm m$处的质点运动路程为$s=4 \times 2\;\rm cm+4 \times 4\;\rm cm=24\;\rm cm$，故$\rm D$错误。

故选：$\rm AC$。