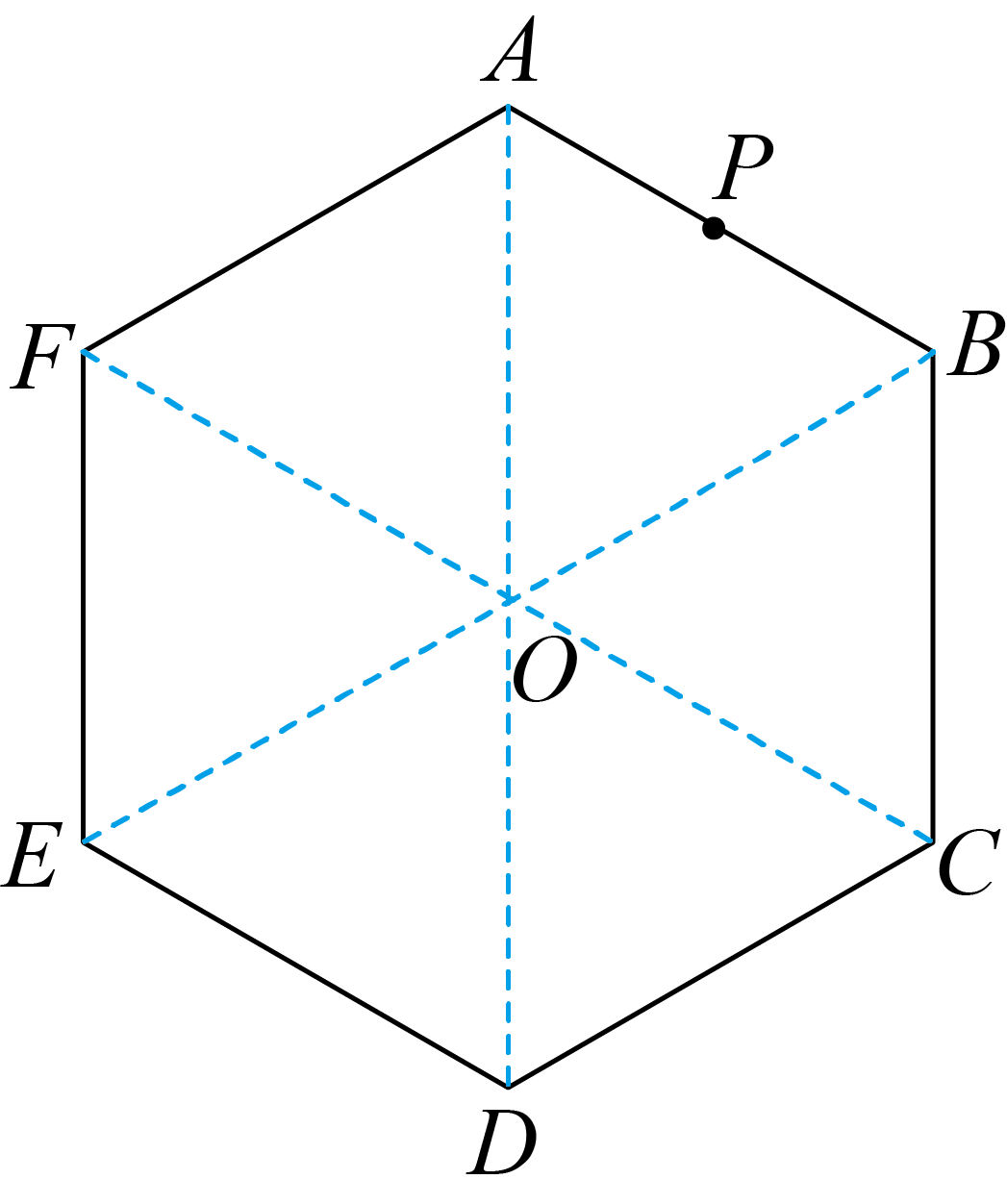
如图，均匀介质中有一个正六边形平面$ABCDEF$，$ P$点为$AB$边中点。在$P$、$D$、$F$三点上各有一个沿垂直纸面方向振动的波源，它们在$t=0\;\rm s$时同时起振，振动情况完全相同，振动周期为$T=2\;\rm s$，$ |AF|=3\lambda$（$\lambda$为所产生机械波波长）。已知该机械波传播$r$远时的振幅$A \propto \dfrac{1}{\sqrt{r}}$，波源$D$所发出的波到达$A$点时的振幅$A=1\;\rm cm$，则：$(\qquad)$

足够长时间后$A$处的质点振动的振幅为$\\left( \\sqrt{2}-1 \\right)\\;\\text{cm}$

足够长时间后$A$处的质点振动的振幅为$\\left( \\sqrt{2}+1 \\right)\\;\\text{cm}$

在$t=0\\;\\rm s$到$t=14\\;\\rm s$内，$A$处的质点运动的路程为$\\left( 32-8\\sqrt{2} \\right)\\;\\text{cm}$

在$t=0\\;\\rm s$到$t=14\\;\\rm s$内，$A$处的质点运动的路程为$\\left( 24-4\\sqrt{2} \\right)\\;\\text{cm}$

$\rm AB$．正六边形平面$ABCDEF$，$P$点为$AB$边中点且$|AF|=3\lambda$，则$PA=1.5\lambda$，$DA=6\lambda$

波源$D$所发出的波到达$A$点时的振幅$A=1\;\rm cm$，且该机械波传播$r$远时的振幅$A \propto \dfrac{1}{\sqrt{r}}$

则波源$F$、$P$所发出的波到达$A$点时的振幅分别为$\sqrt{2}\;\rm cm$和$2\;\rm cm$。

在$P$、$D$、$F$三点上各有一个沿垂直纸面方向振动的波源，它们在$t=0\;\rm s$时同时起振，振动情况完全相同，由振动加强减弱条件可知，波源$D$、$F$所发出的波到达$A$点同步加强，与波源$P$所发出的波正好相反。足够长时间后$A$处的质点振动的振幅为$\left\lbrack \left( \sqrt{2}+1 \right)-2 \right\rbrack \;\rm cm=\left( \sqrt{2}-1 \right)\;\rm cm$，故$\rm A$正确，$\rm B$错误；

$\rm CD$．振动周期为$T=2\;\rm s$，在$t=0\;\rm s$到$t=14\;\rm s$内，总共为$7T$。波源$P$所发出的波到达$A$点时需要$1.5T$，可引起振动时间$5.5T$，波源$F$所发出的波到达$A$点时需要$3T$，可引起振动时间$4T$，波源$D$所发出的波到达$A$点时需要$6T$，可引起振动时间$1T$。$0-1.5T$，$A$处不振动。$1.5T-3T$，$A$处参与波源$P$引起的振动，$S_{1}=1.5 \times 4 \times 2\;\rm cm=12\;\rm cm$

$3T-6T$，$A$处参与波源$P$、$F$引起的振动，$S_{2}=3 \times 4 \times \left( 2-\sqrt{2} \right)\;\rm cm=\left( 24-12\sqrt{2} \right)\;\rm cm$

$6T‐7T$，$A$处参与波源$P$、$D$、$F$引起的振动，$S_{3}=1 \times 4 \times \left( \sqrt{2}-1 \right)\;\rm cm=\left( 4\sqrt{2}-4 \right)\;\rm cm$

在$t=0\;\rm s$到$t=14\;\rm s$内，$A$处的质点运动的路程为$S_{1}+S_{2}+S_{3}=\left( 32-8\sqrt{2} \right)\;\rm cm$，故$\rm C$正确，$\rm D$错误。

故选：$\rm AC$ 。