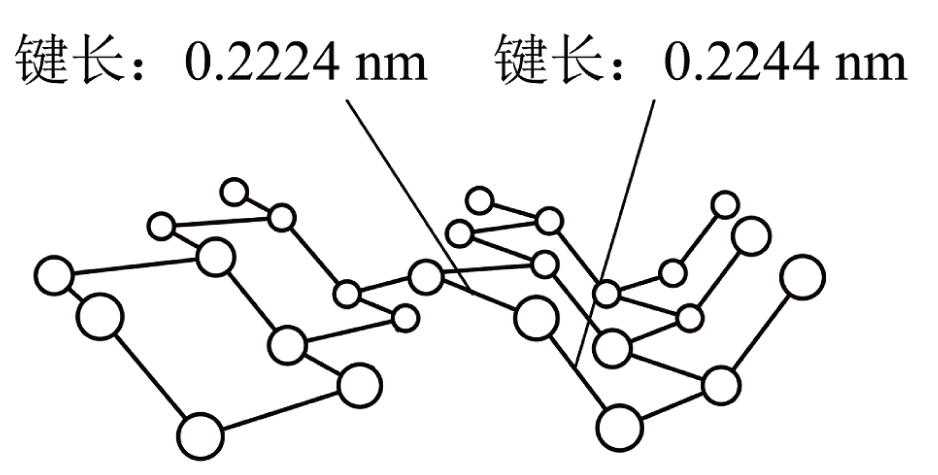
基态磷原子的价电子排布式为                。

$\\text{3}{{\\text{s}}^{\\text{2}}}\\text{3}{{\\text{p}}^{\\text{3}}}$

$\rm P$原子序数$\rm 15$，基态磷原子的价电子排布式：$\text{3}{{\text{s}}^{\text{2}}}\text{3}{{\text{p}}^{\text{3}}}$；

根据图中信息，回答下列问题：

①黑磷晶体中存在的作用力为                。

②黑磷单层中$\text{P}$原子与$\text{P}-\text{P}$键的个数比为                。

分子间相互作用力和共价键；$\\rm 2:3$

①黑磷与石墨的结构类似，说明黑磷晶体层与层间存在分子间相互作用力，层内原子与原子间存在共价键；

②黑磷单层中，每个$\rm P$原子形成$\rm 3$个$\text{P}-\text{P}$键，每个$\text{P}-\text{P}$键由$\rm 2$个$\rm P$原子所共有，则$\text{P}$原子与$\text{P}-\text{P}$键的个数比为$\rm 2: 3$；

下列说法正确的有                $\rm ($填字母$\rm )$。

$\rm a$．黑磷中$\rm \text{P}$采取$\rm \mathrm{sp}^2$杂化

$\rm b$．黑磷单层中$\rm \text{P}-\text{P}$键的键能不完全相同

$\rm c$．黑磷与石墨都属于混合型晶体

$\\rm bc$

$\rm a$．黑磷中$\rm \text{P}$形成$\rm 3$个$\rm \sigma $键，存在$\rm 1$对孤电子对，采取$\rm \text{s}{{\text{p}}^{\text{3}}}$杂化，$\rm a$错误；

$\rm b$．黑磷单层中$\rm \text{P}-\text{P}$键键长不完全相同，则键能不完全相同，$\rm b$正确；

$\rm c$．黑磷与石墨都属于混合型晶体，$\rm c$正确；

答案选$\rm bc$；

$\rm I$$\rm I$．砷化镓$\rm \left( \text{GaAs} \right)$是最重要的第二代半导体，被广泛应用于光电子和通信等领域。

$\text{Ga}$与$\text{VA}$族元素$\text{N}\text{P}\text{As}$能形成结构相似的化合物$\text{GaN}$、$\text{GaP}$、$\text{GaAs}$，它们在熔融态下均不导电，熔点如下表所示。分析$\text{GaN}$、$\text{GdP}$、$\text{GaAs}$的熔点依次降低的原因为                。

$\\text{GaN}$、$\\text{GdP}$、$\\text{GaAs}$均为共价晶体，$\\rm N$、$\\rm P$、$\\rm As$原子半径逐渐增大，键长逐渐增长，键能逐渐减小，熔点依次降低

$\text{GaN}$、$\text{GdP}$、$\text{GaAs}$均为共价晶体，$\rm N$、$\rm P$、$\rm As$原子半径逐渐增大，键长逐渐增长，键能逐渐减小，熔点依次降低；

$\text{GaAs}$的晶胞结构如图甲所示，将$\text{Mn}$掺杂到$\text{GaAs}$晶体中得到新型材料如图乙所示。

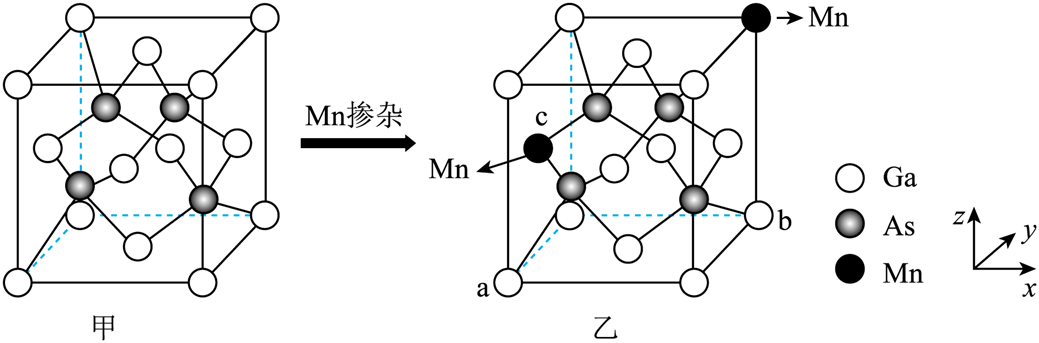
①图甲中，$\text{GaAs}$的相对质量为$\text{M}$，晶体密度为$\rho\rm \;{ g\cdot c}{{\text{m}}^{-3}}$，阿伏伽德罗常数为${{N}_{\text{A}}}$，则晶胞边长$a=$                $\mathrm{nm}$。$\rm ($列出计算式。$1\;\rm \text{nm}={{10}^{-7}}\;\rm \text{cm}$

②图乙中，掺杂$\text{Mn}$之后的原子个数比$ {N}\left( \text{Ga} \right): {N}\left( \text{As} \right): {N}\left( \text{Mn} \right)=$                。

$\\sqrt[3]{\\dfrac{{4M}}{\\rho{ }{{{N}}_{\\rm {A}}}}}\\times {{10}^{7}}$；$\\rm 5: 27: 32$

①根据均摊法计算原子个数，$\rm Ga$个数为$8\times \dfrac{1}{8}+6\times \dfrac{1}{2}=4$，$\rm As$位于晶胞内部，有$\rm 4$个，$\rm {GaAs}$的相对质量为${M}$，晶体密度为$\rho \;\rm{g\cdot c}{{{m}}^{-3}}$，根据晶胞密度计算公式：$\rho =\dfrac{{NM}}{{{{N}}_{\rm {A}}}{V}}$，算得边长$a=\sqrt[3]{\dfrac{{4M}}{{ }\rho{{{N}}_{\rm {A}}}}}\times {{10}^{7}}\;\rm {nm}$；

②掺杂$\rm {Mn}$之后，$\rm As$原子个数不变，将$\rm 1$个顶点$\rm Ga$和$\rm 1$个面心$\rm Ga$替换成$\rm Mn$，$\rm Mn$原子个数：$1\times \dfrac{1}{8}+1\times \dfrac{1}{2}=\dfrac{5}{8}$，$\rm Ga$原子个数：$4-\dfrac{5}{8}=\dfrac{27}{8}$，则${N}\left(\rm {Ga} \right):{N}\left(\rm {As} \right):{N}\left(\rm {Mn} \right)=5:27:32$。