下列状态的镁中，电离最外层一个电子所需能量最大的是                $\rm ($填标号$\rm )$。

$\rm A$．$\left[ \text{Ne} \right]3{{\text{s}}^{1}}$   $\rm B$．$\left[ \text{Ne} \right]3{{\text{s}}^{2}}$   $\rm C$．$\left[ \text{Ne} \right]3{{\text{s}}^{1}}3{{\text{p}}^{1}}$   $\rm D$．$\left[ \text{Ne} \right]3{{\text{p}}^{1}}$

$\\rm A$

$\rm A$.图示电离最外层一个电子所需能量为$\rm Mg$的第二电离能；

$\rm B$.图示电离最外层一个电子所需能量为$\rm Mg$的第一电离能；

$\rm C$.图示为镁原子激发态，容易失去一个电子；

$\rm D$.图示为$\rm Mg^{+}$激发态，较$\rm A$项容易失去一个电子；

综上，电离最外层一个电子所需能量最大的是$\rm A$；

乙二胺$\left( {{\text{H}}_{2}}\text{NC}{{\text{H}}_{2}}\text{C}{{\text{H}}_{2}}\text{N}{{\text{H}}_{2}} \right)$是一种有机化合物，分子中氮、碳的杂化类型分别是                、                。乙二胺能与$\text{M}{{\text{g}}^{2+}}$、$\text{C}{{\text{u}}^{2+}}$等金属离子形成稳定环状离子，乙二胺中提供孤电子对的是                原子$\rm ($填名称$\rm )$，其中与乙二胺形成的化合物稳定性相对较高的是                $\rm ($填“$\text{M}{{\text{g}}^{2+}}$”或“$\text{C}{{\text{u}}^{2+}}$”$\rm )$。

$\\rm sp^{3}$ ； $\\rm sp^{3}$ ； $\\rm N$ ； $\\rm Cu^{2+}$

在该有机物中，氮原子周围形成三个单键，且存在一个孤电子对，因此氮的杂化类型为$\rm sp^{3}$杂化；碳原子周期形成四个单键，因此碳的杂化类型为$\rm sp^{3}$杂化；

乙二胺中的两个$\rm N$提供孤电子对给金属离子形成稳定的配位键，故答案为$\rm N$原子；

由于$\rm Cu^{2+}$的半径大于$\rm Mg^{2+}$的半径，因此$\rm Cu^{2+}$与乙二胺形成的配合物稳定性相对较高；

一些氧化物的熔点如下表所示：

请解释表中非金属氧化物之间熔点差异的原因                。

$\\rm Li_{2}O$和$\\rm MgO$为离子晶体，$\\rm P_{4}O_{6}$和$\\rm SO_{2}$为分子晶体，晶格能$\\rm MgO\\gt Li_{2}O$，分子间作用力$\\rm P_{4}O_{6}\\gt SO_{2}$

$\rm Li_{2}O$和$\rm MgO$为离子晶体，$\rm P_{4}O_{6}$和$\rm SO_{2}$为分子晶体，离子晶体的熔点比分子晶体的熔点高；在离子晶体中，晶格能越大，熔点越高，由于晶格能$\rm MgO\gt Li_{2}O$，因此$\rm MgO$的熔点高于$\rm Li_{2}O$；在分子晶体中，分子间作用力越大，熔点越高，由于分子间作用力$\rm P_{4}O_{6}\gt SO_{2}$， 因此$\rm P_{4}O_{6}$的熔点高于$\rm SO_{2}$；

图$\left( \text{a} \right)$是$\text{MgC}{{\text{u}}_{2}}$的拉维斯结构，$\text{Mg}$以金刚石方式堆积，八面体空隙和半数的四面体空隙中，填入以四面体方式排列的$\text{Cu}$。图$\left( \text{b} \right)$是沿立方格子对角面取得的截图。可见，$\text{Mg}$原子之间最短距离$y=$                $\text{pm}$。设阿伏加德罗常数的值为${{N}_{\text{A}}}$，则$\text{MgC}{{\text{u}}_{2}}$的密度是                $\text{g}\cdot \text{c}{{\text{m}}^{-3}}\rm ($列出计算表达式$\rm )$。

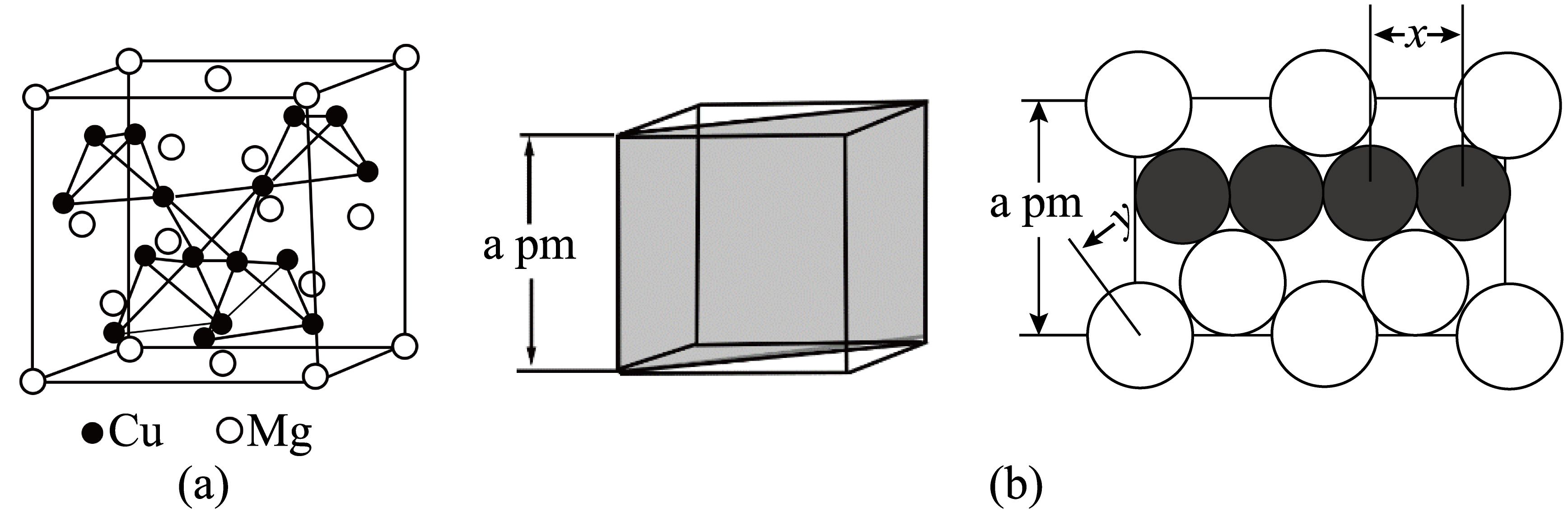
$\\dfrac{\\sqrt{\\text{3}}}{\\text{4}}a\\,\\text{pm}$ ； $\\dfrac{8\\times 24+16\\times 64}{{{N}_{\\text{A}}}{{a}^{3}}\\times {{10}^{-30}}}$

如图所示，，$\rm CD$距离为$y$，该长度为体对角线$\rm BC$长度的$\dfrac{1}{4}=\dfrac{1}{4}\times \sqrt{3}\times a\,\text{pm}=\dfrac{\sqrt{\text{3}}}{\text{4}}a\,\text{pm}$；该晶胞中$\rm Mg$原子位于$\rm 8$个顶点上，$\rm 6$个面心上，在晶胞内部有$\rm 4$个$\rm Mg$原子，所以$\rm Mg$原子个数$=8\times \dfrac{1}{8}+6\times \dfrac{1}{2}+4=8$，$\rm Cu$原子位于晶胞内部，有$\rm 16$个；晶胞体积$={{\text{(}a\times \text{1}{{\text{0}}^{\text{-10}}}\,\text{cm)}}^{\text{3}}}$，晶胞密度$=\dfrac{m}{V}=\dfrac{\dfrac{8\times 24+16\times 64}{{{N}_{\text{A}}}}}{{{(a\times {{10}^{-10}})}^{3}}}\,\text{g/c}{{\text{m}}^{\text{3}}}=\dfrac{8\times 24+16\times 64}{{{N}_{\text{A}}}{{a}^{3}}\times {{10}^{-30}}}\,\text{g/c}{{\text{m}}^{\text{3}}}$。