$\text{C}{{\text{O}}_{\text{2}}}$催化加氢合成二甲醚的热化学方程式为                ，该反应自发进行的条件为                。

$2\\text{C}{{\\text{O}}_{2}}\\left( \\text{g} \\right)+6{{\\text{H}}_{2}}\\left( \\text{g} \\right)\\rightleftharpoons \\text{C}{{\\text{H}}_{3}}\\text{OC}{{\\text{H}}_{3}}\\left( \\text{g} \\right)+3{{\\text{H}}_{2}}\\text{O}\\left( \\text{g} \\right)\\quad \\Delta H=-122.5\\ \\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$；低温

则依据盖斯定律可知由“反应①$\rm \times 2+$反应②”即得到反应$2\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+6{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OC}{{\text{H}}_{3}}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\quad \Delta H=\left( +41.2\times 2-204.9 \right)\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}=-122.5\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

反应$2\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+6{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OC}{{\text{H}}_{3}}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)$是熵减小的放热反应，依据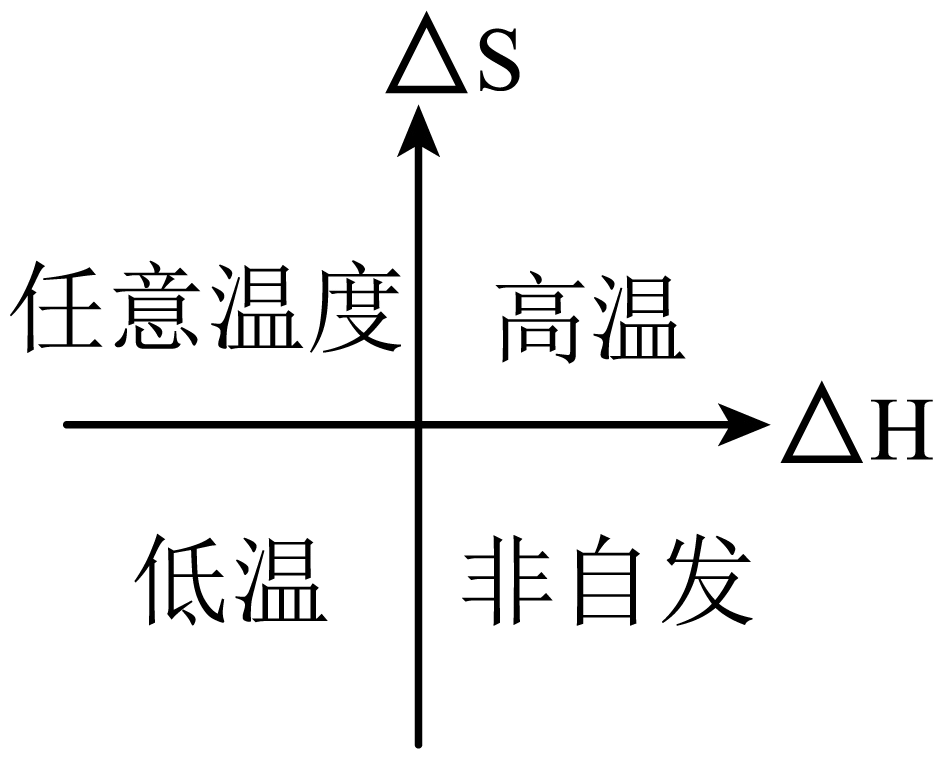得到自发条件为低温；

在恒压、$\text{C}{{\text{O}}_{\text{2}}}$和${{\text{H}}_{\text{2}}}$的起始量一定的条件下，$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率和平衡时$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}$的选择性随温度变化如图。其中，$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}的选择性\mathrm{}=\dfrac{2\times \text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}的物质的量}}{反应的\text{C}{{\text{O}}_{2}}的物质的量}\times 100\%$

当温度高于$\rm 300\;\rm ^\circ\rm C$，$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率随温度升高而上升的原因是                。若起始投料比为${n}\left( {{\text{H}}_{\text{2}}} \right){:n}\left( \text{C}{{\text{O}}_{\text{2}}} \right)\text{=3:1}$，不考虑其他副反应，则$\rm 288\;\rm ^\circ\rm C$时，反应①的化学平衡常数$ K=$                $\rm (33.3\%\approx \dfrac{1}{3}\rm )$。

反应①的$\\Delta H\\gt 0$，$\\text{C}{{\\text{O}}_{\\text{2}}}$转化为$\\text{C}{{\\text{H}}_{\\text{3}}}\\text{OC}{{\\text{H}}_{\\text{3}}}$的反应的$\\Delta H\\lt 0$，温度升高，使$\\text{C}{{\\text{O}}_{\\text{2}}}$转化为$\\rm CO$的平衡转化率上升，而使$\\text{C}{{\\text{O}}_{\\text{2}}}$转化为$\\text{C}{{\\text{H}}_{\\text{3}}}\\text{OC}{{\\text{H}}_{\\text{3}}}$的平衡转化率下降，且上升幅度超过下降幅度； $\\rm 0.04$

反应①的$\Delta H\gt 0$，$\text{C}{{\text{O}}_{\text{2}}}$转化为$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}$的反应的$\Delta H\lt 0$，温度升高，使$\text{C}{{\text{O}}_{\text{2}}}$转化为$\rm CO$的平衡转化率上升，而使$\text{C}{{\text{O}}_{\text{2}}}$转化为$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}$的平衡转化率下降，且上升幅度超过下降幅度；$\rm 288\;\rm ^\circ\rm C$时，二甲醚的选择性是$\rm 0.333$，二氧化碳的平衡转化率是$\rm 0.3$，设起始时氢气是$\rm 3\;\rm mol$、二氧化碳是$\rm 1\;\rm mol$，则$\begin{matrix} {} \\ \\ \\ \\ \end{matrix}\begin{matrix} \text{C}{{\text{O}}_{2}}(\text{g}) \\ 开始1\;\rm \text{mol} \\转化 {x{\rm mol}} \\平衡\ \ \ \ \ \ \ \ \ {} \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} {{\text{H}}_{2}}(\text{g}) \\ 3\; \text{mol} \\ {x{\rm mol}} \\ {} \\ \end{matrix}\begin{matrix} \rightleftharpoons \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{CO}(\text{g}) \\ 0 \\ {x\ \rm mol} \\ {x\rm\ {mol}} \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} {{\text{H}}_{2}}\text{O}(\text{g}) \\ 0 \\ {x\rm\ mol} \\ {x\rm\ mol} \\ \end{matrix}$，$\begin{matrix} {} \\ \\ \\ \\ \end{matrix}\begin{matrix} \text{2C}{{\text{O}}_{2}}(\text{g}) \\开始 1\; \text{mol} \\ 转化{2y\rm\ mol} \\ {}平衡\ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{6}{{\text{H}}_{2}}(\text{g}) \\ 3\;\rm \text{mol} \\ 6{y\rm \ mol} \\ {} \\ \end{matrix}\begin{matrix} \rightleftharpoons \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{C}{{\text{H}}_{3}}\text{OC}{{\text{H}}_{3}}(\text{g}) \\ 0 \\ \text{y\rm \ mol} \\ \text{y\rm \ mol} \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{3}{{\text{H}}_{2}}\text{O}(\text{g}) \\ 0 \\ {3y\rm \ \rm \rm mol} \\ {3y\rm \ mol} \\ \end{matrix}$，因此，$\dfrac{{x+2y}}{1}\text{=0}{.3}$，${y}=\dfrac{0.3\times 0.333}{2}$，解得${x}\approx \text{0}\text{.2}$、${y}\approx 0.05$，平衡时二氧化碳物质的量为$\rm 0.7\;\rm mol$，氢气物质的量为$\rm 2.5\;\rm mol$，$\rm CO$物质的量为$\rm 0.2\;\rm mol$，水物质的量为$\rm 0.35\;\rm mol$，反应①的前后体积不变，则其平衡常数$K=\dfrac{0.2\times 0.35}{0.7\times 2.5}=0.04$；故答案为：反应①的$\Delta H\gt 0$，$\text{C}{{\text{O}}_{\text{2}}}$转化为$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}$的反应的$\Delta H\lt 0$，温度升高，使$\text{C}{{\text{O}}_{\text{2}}}$转化为$\rm CO$的平衡转化率上升，而使$\text{C}{{\text{O}}_{\text{2}}}$转化为$\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}$的平衡转化率下降，且上升幅度超过下降幅度；$\rm 0.04$。

Ⅱ$\rm .$由$\text{C}{{\text{O}}_{\text{2}}}$制备二甲醚的另一种方法为先合成甲醇，再经脱水，主要分为以下步骤。

反应③：$\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\quad \Delta H_{3}\lt 0$

反应④：$\text{2C}{{\text{H}}_{\text{3}}}\text{OH}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}\left( \text{g} \right)+{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right)\quad \Delta {{H}_{4}}\gt 0$

在不同的压强下，按照${n}\left( \text{C}{{\text{O}}_{\text{2}}} \right){:n}\left( {{\text{H}}_{\text{2}}} \right)\text{=1:3}$投料比合成甲醇，实验测定$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率和$\text{C}{{\text{H}}_{\text{3}}}\text{OH}$的平衡产率随温度的变化关系如图甲或乙所示。

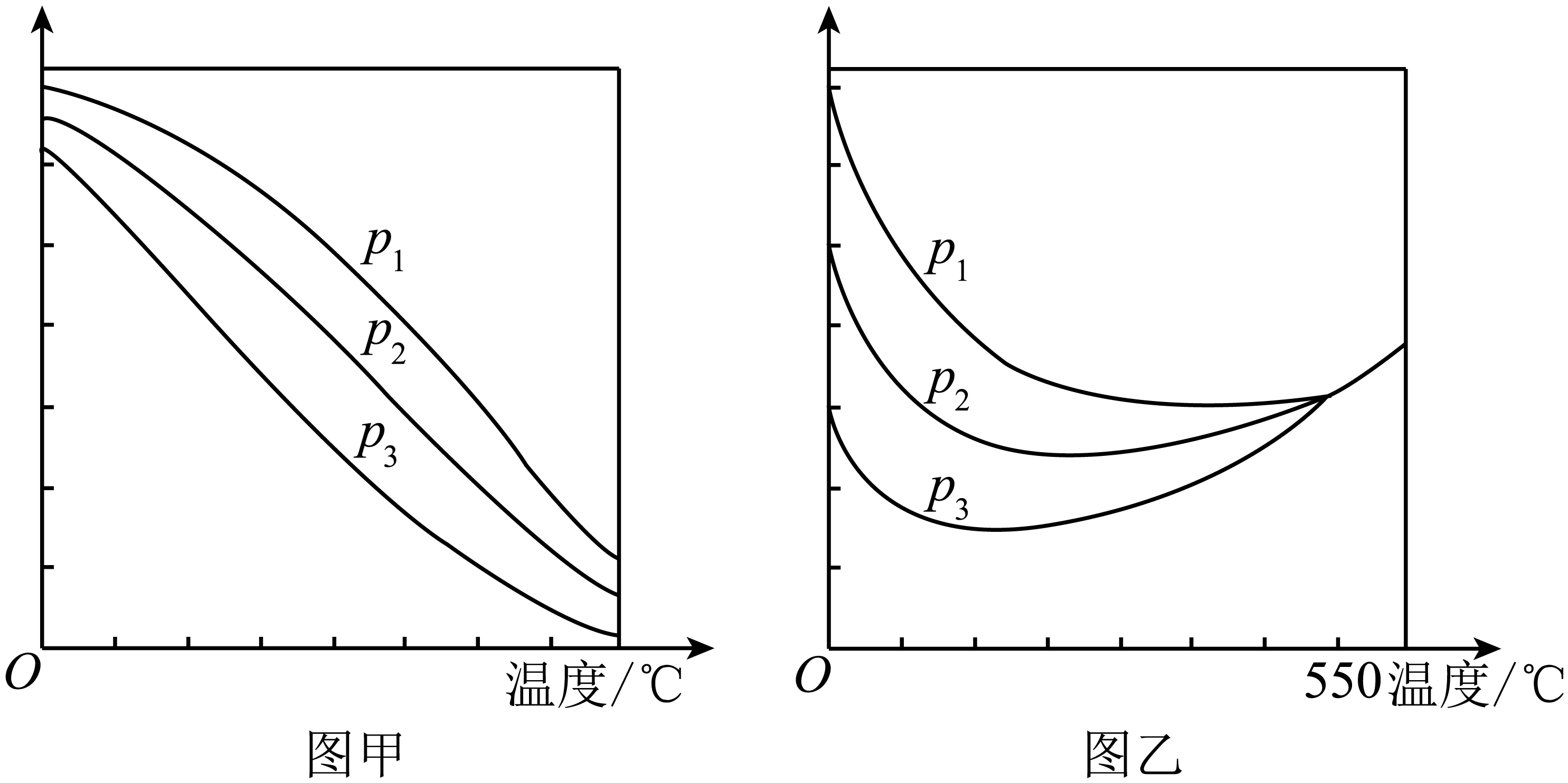
下列说法正确的是$(\quad\ \ \ \ )\rm ($填字母$\rm )$。

图甲的纵坐标表示$\\text{C}{{\\text{H}}_{\\text{3}}}\\text{OH}$的平衡产率

压强：${{p}_{1}}\\lt {{p}_{2}}\\lt {{p}_{3}}$

为了同时提高$\\text{C}{{\\text{O}}_{\\text{2}}}$的平衡转化率和$\\text{C}{{\\text{H}}_{\\text{3}}}\\text{OH}$的平衡产率，应选择高温、高压的反应条件

一定温度、压强下，寻找活性更高的催化剂，是提高$\\text{C}{{\\text{O}}_{\\text{2}}}$的平衡转化率的主要研究方向

$\rm A$．温度升高，反应③的平衡逆向移动，反应④的平衡正向移动，$\text{C}{{\text{H}}_{\text{3}}}\text{OH}\rm (g)$的平衡产率会降低，所以图甲的纵坐标表示$\text{C}{{\text{H}}_{\text{3}}}\text{OH}$的平衡产率；$\rm B$．反应③的正反应是气体体积减小的反应，在其他条件不变时，增大压强，化学平衡正向移动、$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率增大，$\text{C}{{\text{H}}_{\text{3}}}\text{OH}$的平衡产率增大，压强${{p}_{1}}\gt {{p}_{2}}\gt {{p}_{3}}$；$\rm C$．反应③的正反应是气体体积减小的放热反应，为了同时提高$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率和$\text{C}{{\text{H}}_{\text{3}}}\text{OH}$的平衡产率，根据平衡移动原理，可知应选择低温、高压的反应条件，故$\rm C$错误；$\rm D$．一定温度、压强下，寻找活性更高的催化剂，可以加快化学反应速率，但化学平衡不发生移动，因此不能提高$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率。

压强为$\rm 4\ MPa$，当${n}\left( \text{C}{{\text{O}}_{\text{2}}} \right){:n}\left( {{\text{H}}_{\text{2}}} \right)\text{=1:3}$的混合气体以一定流速通过装有某种催化剂的反应器。在$\rm 280\;\rm ^\circ\rm C$时，若$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率为$\rm 7.00\%$，甲醇的选择性为$\rm 95.0\%$，则甲醇的收率为                

$\rm (甲醇的收率=\dfrac{甲醇的生成量}{二氧化碳的进料量}\times 100\%\rm )$。

$\\rm 6.65\\%$

当${n}\left( \text{C}{{\text{O}}_{2}} \right):{n}\left( {{\text{H}}_{2}} \right)=1:3$，假设${n}\left( \text{C}{{\text{O}}_{2}} \right)=1\ \text{mol}$，$\text{C}{{\text{O}}_{\text{2}}}$的平衡转化率为$\rm 7.00\%$，则${{{n}}_{}}\left( \text{C}{{\text{O}}_{2}} \right)=0.07 \text{\ mol}$，甲醇的选择性为$\rm 95.0\%$，则$\dfrac{{n}\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)}{0.07}\times 100\%=95\%$，${n}\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)=0.0665\ \text{mol}$，故甲醇的收率为$\dfrac{0.0665}{1}\times 100\%=6.65\%$；

甲醇脱水若条件控制不当可生成丙烯，反应为$3\text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)\to {{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)+3{{\text{H}}_{2}}\text{O}\left( \text{g} \right)$，反应的$\rm Arrhenius$经验公式的实验数据如图曲线所示，已知$\rm Arrhenius$经验公式为$\text{R}\ln k=-\dfrac{{{E}_{\text{a}}}}{{T}}+{C}\rm ($其中，${{E}_{\text{a}}}$为活化能，$ k$为速率常数，$ R$和$ C$为常数$\rm )$。该反应的活化能${{E}_{\text{a}}}=$                $\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。

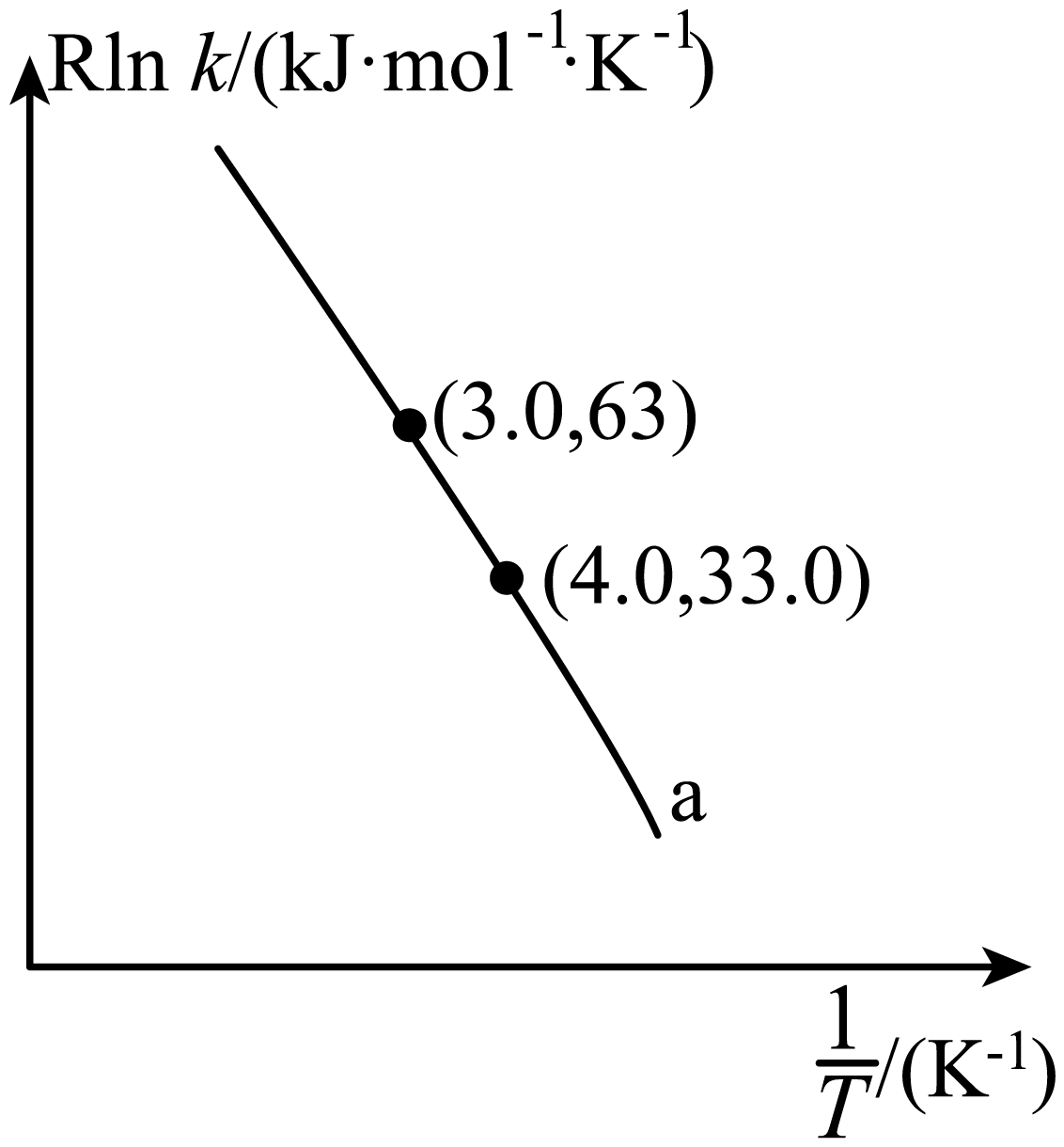
$\\rm 30$

根据图像可知$63=-3{{E}_{\text{a}}}+\text{C}$、$33=-4{{E}_{\text{a}}}+\text{C}$，解得该反应的活化能${{E}_{\text{a}}}=30\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。