工业上，利用$\text{CO}$加氢合成$\text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)$的热化学方程式为                。

$2{{\\text{H}}_{2}}\\left( \\text{g} \\right)+\\text{CO}\\left( \\text{g} \\right)\\rightleftharpoons \\text{C}{{\\text{H}}_{3}}\\text{OH}\\left( \\text{g} \\right)\\quad \\Delta H=-91.5\\ \\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$

根据盖斯定律，反应$\rm ii-iii$可得$2{{\text{H}}_{2}}\left( \text{g} \right)+\text{CO}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)$，则该反应的$\Delta H=(-49.9\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}})-(+41.6\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}})=-91.5\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，则利用$\text{CO}$加氢合成$\text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)$的热化学方程式为：$2{{\text{H}}_{2}}\left( \text{g} \right)+\text{CO}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)\quad \Delta H=-91.5\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

向反应器中充入$1\ \text{mol}\,\text{C}{{\text{O}}_{2}}$和$3\ \text{mol}\,{{\text{H}}_{2}}$，在催化剂$\text{Cat}1$、$\text{Cat}2$作用下发生上述反应，测得相同时间内$\text{C}{{\text{O}}_{2}}$的转化率与温度关系如图所示。温度低于$\rm 450\;\rm ^\circ\rm C$时，催化效率较高的催化剂是                $\rm ($填“$\text{Cat}1$”或“$\text{Cat}2$”$\rm )$，随着温度升高，$\text{Cat}1$、$\text{Cat}2$曲线相交，其主要原因可能是                。

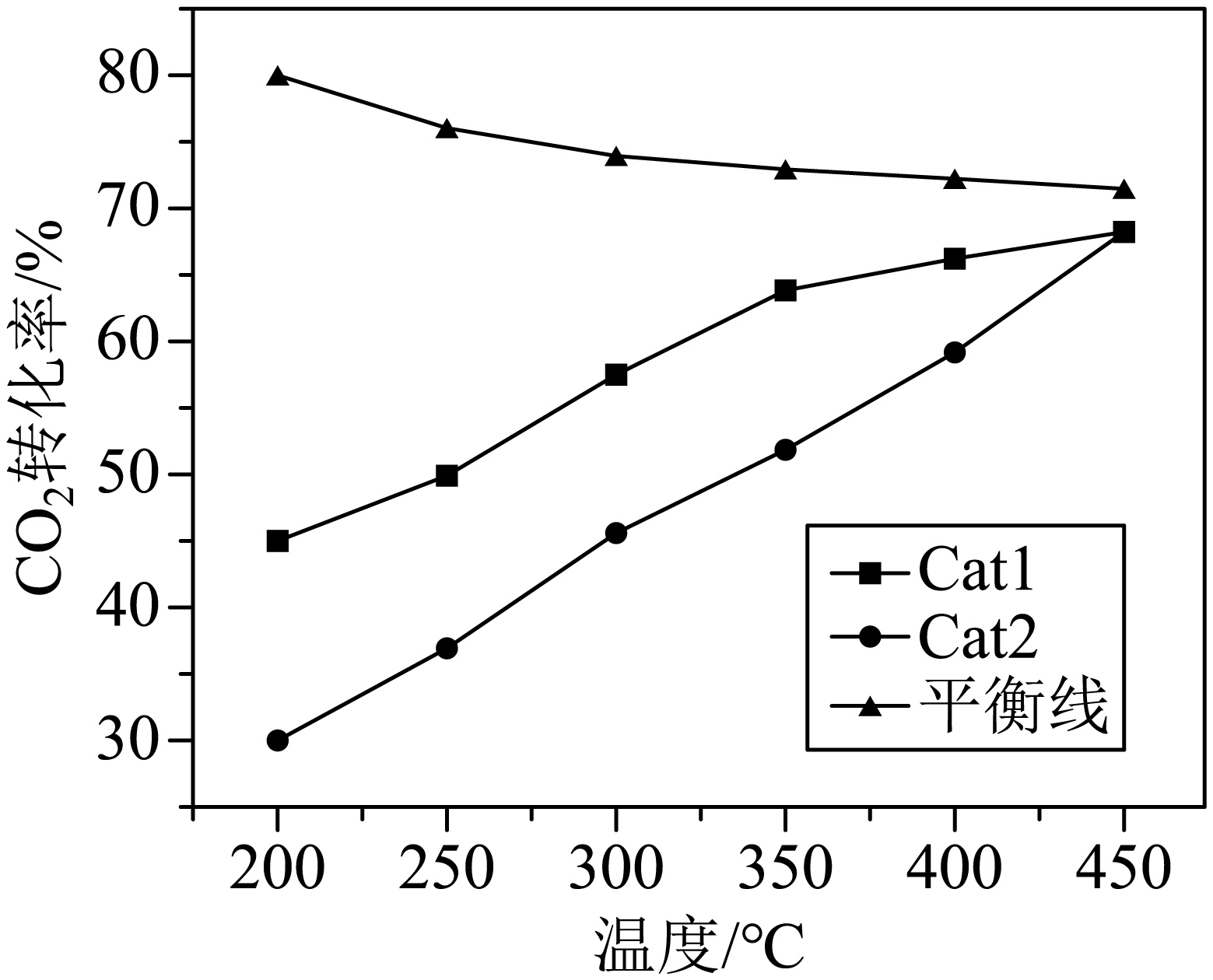
$\\text{Cat}1$ ； 随着温度升高，温度对反应速率起决定作用

由图可知，温度低于$\rm 450\;\rm ^\circ\rm C$时，催化剂是$\text{Cat}1$时，二氧化碳的转化率高，故此时催化效率较高的催化剂是；由于反应时间相同，随着温度升高，反应速率加快，则随着温度升高，$\text{Cat}1$、$\text{Cat}2$曲线相交，其主要原因可能是：随着温度升高，温度对反应速率起决定作用；

某温度下，向恒容密闭容器中充入$1\ \text{mol}\,\text{C}{{\text{O}}_{2}}$和$3\ \text{mol}\,{{\text{H}}_{2}}$，发生上述反应$\rm i$、$\rm ii$、$\rm iii$，起始压强为$100\,\text{kPa}$，达到平衡时$\text{C}{{\text{O}}_{2}}$转化率为$\rm 60\%$，$\text{C}{{\text{H}}_{3}}\text{C}{{\text{H}}_{2}}\text{OH}$选择性为$\rm 50\%$，$\text{CO}$选择性为$\rm 25\%$。

已知：乙醇的选择性$=\dfrac{n\left( {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH} \right)}{n\left( {{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH} \right)+n\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)+n\left( \text{CO} \right)}\times 100\%\rm (\text{C}{{\text{H}}_{3}}\text{OH}$、$\text{CO}$的选择性同理$\rm )$。$\rm )$

该温度下，反应$\rm iii$的平衡常数${{K}_{\text{p}}}=$                $\rm ($用分数表示，用分压计算的平衡常数为压强平衡常数，分压等于总压$\rm \times $物质的量分数$\rm )$。

$\\dfrac{1}{7}$

根据相关数据，达到平衡时$\text{C}{{\text{O}}_{2}}$转化率为$\rm 60\%$，$\text{C}{{\text{H}}_{3}}\text{C}{{\text{H}}_{2}}\text{OH}$选择性为$\rm 50\%$，$\text{CO}$选择性为$\rm 25\%$，根据原子守恒可计算各组分物质的量如下：

气体总物质的量为$3.0\ \text{mol}$。对于等分子数反应，可用物质的量替代分压计算平衡常数，反应$\rm iii$的平衡常数${{K}_{\text{p}}}=\dfrac{p\left( \text{CO} \right)\cdot p\left( {{\text{H}}_{2}}\text{O} \right)}{p\left( \text{C}{{\text{O}}_{2}} \right)\cdot p\left( {{\text{H}}_{2}} \right)}=\dfrac{0.1\ \text{mol}\times 0.8\ \text{mol}}{0.4\ \text{mol}\times 1.4\ \text{mol}}=\dfrac{1}{7}$；

$\text{C}{{\text{O}}_{2}}$与${{\text{H}}_{2}}$在活化后的催化剂$\rm [$催化剂活化：$\text{I}{{\text{n}}_{2}}{{\text{O}}_{3}}\rm ($无活性$)\overset{还原}{\underset{氧化}{\rightleftharpoons}}\text{I}{{\text{n}}_{2}}{{\text{O}}_{3-x}}\rm .($有活性$\rm )]$表面可逆地发生反应$\rm ii$，其反应历程如图所示。

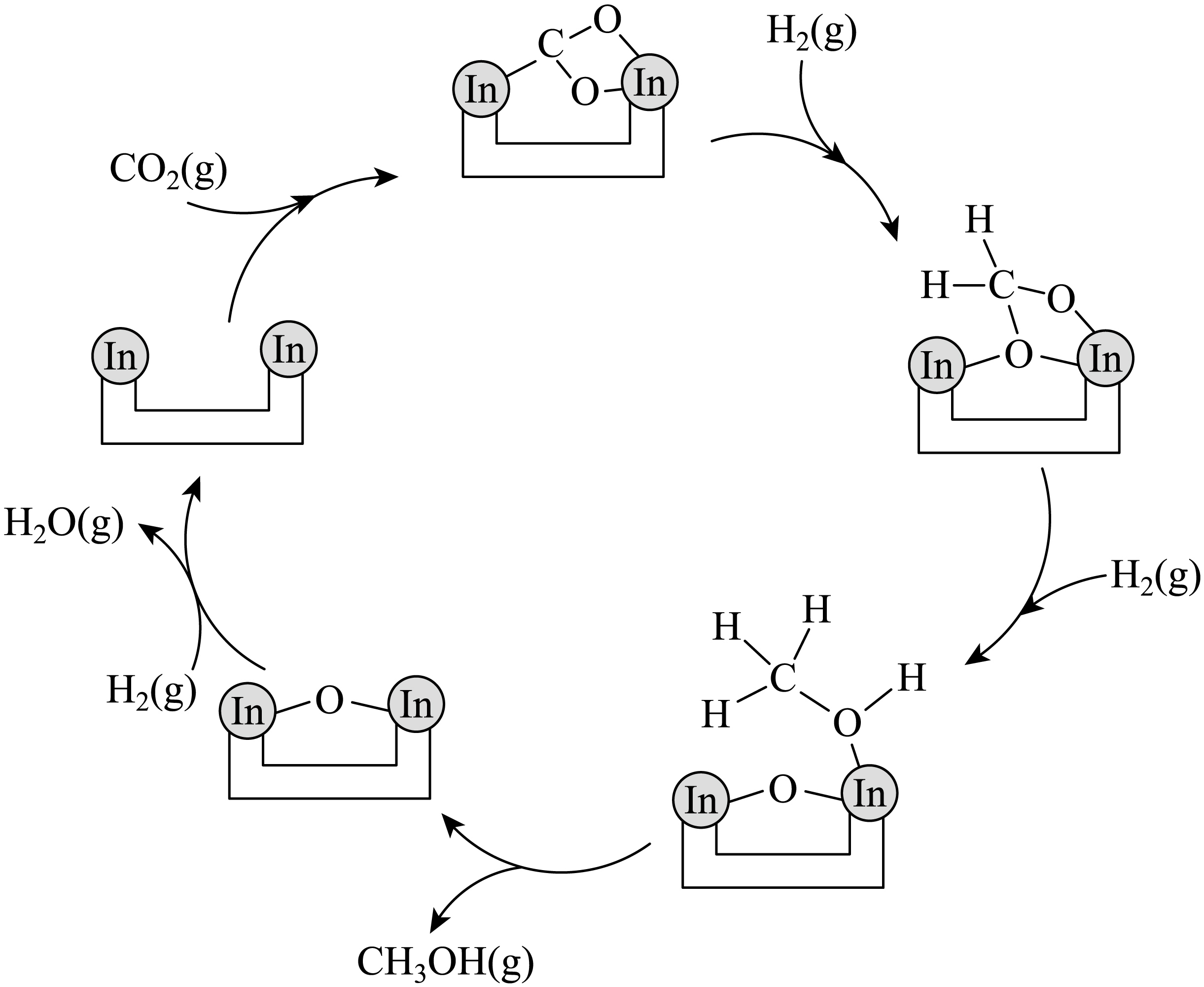
①对于$\text{C}{{\text{O}}_{2}}$制甲醇的过程，以下描述正确的是                $\rm ($填字母$\rm )$。

$\rm A$．反应中经历了$\text{In}-\text{C}$、$\text{In}-\text{O}$键的形成和断裂

$\rm B$．加压可以提高$\text{C}{{\text{O}}_{2}}$的平衡转化率

$\rm C$．升高温度有利于生成甲醇

②$\text{C}{{\text{O}}_{2}}$与${{\text{H}}_{2}}$混合气体以不同的流速通过反应器，流速加快可减少产物中${{\text{H}}_{2}}\text{O}$的积累，减少反应                $\rm ($用化学方程式表示$\rm )$的发生，减少催化剂的失活，提高甲醇选择性。

$\\rm AB$ ； $\\text{I}{{\\text{n}}_{2}}{{\\text{O}}_{3-x}}+x{{\\text{H}}_{2}}\\text{O}\\rightleftharpoons \\text{I}{{\\text{n}}_{2}}{{\\text{O}}_{3}}+x{{\\text{H}}_{2}}$

①$\rm A$．由图可知，反应中经历了$\text{In}-\text{C}$、$\text{In}-\text{O}$键的形成和断裂，$\rm A$项正确；

$\rm B$．$\text{C}{{\text{O}}_{2}}$制甲醇是气体分子数减小的反应，加压平衡正向移动，可以提高$\text{C}{{\text{O}}_{2}}$的平衡转化率，$\rm B$项正确；

$\rm C$．$\text{C}{{\text{O}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OH}\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\quad \Delta H=-49.9\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$是放热反应，升高温度平衡逆向移动，不利于生成甲醇，$\rm C$项错误；

故选：$\rm AB$；

②已知催化剂活化：$\text{I}{{\text{n}}_{2}}{{\text{O}}_{3}}\rm ($无活性$)\overset{还原}{\underset{氧化}{\rightleftharpoons}}\text{I}{{\text{n}}_{2}}{{\text{O}}_{3-x}}\rm ($有活性$\rm )$，流速加快可减少产物中${{\text{H}}_{2}}\text{O}$的积累，减少反应$\text{I}{{\text{n}}_{2}}{{\text{O}}_{3-x}}+x{{\text{H}}_{2}}\text{O}\rightleftharpoons \text{I}{{\text{n}}_{2}}{{\text{O}}_{3}}+x{{\text{H}}_{2}}$的发生，减少催化剂的失活，提高甲醇选择性；

用电解法也可以实现由$\text{C}{{\text{O}}_{2}}$制备乙醇。电解时电解质溶液显酸性，阴极的电极反应式为                。

$2\\text{C}{{\\text{O}}_{2}}+12{{\\text{H}}^{+}}+12{{\\text{e}}^{-}}={{\\text{C}}_{2}}{{\\text{H}}_{5}}\\text{OH}+3{{\\text{H}}_{2}}\\text{O}$

根据题意，电解时，二氧化碳在阴极得到电子生成乙醇，电极反应式为：$2\text{C}{{\text{O}}_{2}}+12{{\text{H}}^{+}}+12{{\text{e}}^{-}}={{\text{C}}_{2}}{{\text{H}}_{5}}\text{OH}+3{{\text{H}}_{2}}\text{O}$；

干冰$\rm ($固态$\text{C}{{\text{O}}_{2}}\rm )$的立方晶胞结构中，$\text{C}{{\text{O}}_{2}}$处于顶点和面心，若晶胞参数为$a\ \text{nm}$，${{N}_{\text{A}}}$表示阿伏加德罗常数的值，则干冰晶体的密度为                $\text{g}\cdot \text{c}{{\text{m}}^{-3}}$。

$\\dfrac{1.76\\times {{10}^{23}}}{{{a}^{3}}{{N}_{\\text{A}}}}$

干冰$\rm ($固态$\text{C}{{\text{O}}_{2}}\rm )$的立方晶胞结构中，$\text{C}{{\text{O}}_{2}}$处于顶点和面心，，则每个干冰晶胞中含有$\rm 4$个$\text{C}{{\text{O}}_{2}}$，干冰晶体的密度$ =\dfrac{4\,\text{mol}\times 44\,\text{g}/\text{mol}}{{{(a\times {{10}^{-7}})}^{3}}{{N}_{\text{A}}}}=\dfrac{1.76\times {{10}^{23}}}{{{a}^{3}}{{N}_{\text{A}}}}\,\text{g}\cdot \text{c}{{\text{m}}^{-3}}$。