$\text{C}(\text{s})$摩尔燃烧焓$\Delta {{H}_{5}}=$                $\rm ($用含$\Delta\!\!\text{ }{{\textit{H}}_{\text{1}}}$、$\Delta\!\!\text{ }{{\textit{H}}_{\text{2}}}$、$\Delta\!\!\text{ }{{\textit{H}}_{\text{4}}}$的代数式表示$\rm )$。根据以上数据，摩尔燃烧焓：$\text{CO}(\text{g})$                $\mathrm{H}_{2}(\mathrm{g})\rm ($㙋“$\rm \gt $”，“$\rm =$”，“$\rm \lt $”或“无法判断”$\rm )$。

$\\text{2 }\\!\\!\\Delta\\!\\!\\text{ }{{\\textit{H}}_{\\text{4}}}-\\!\\!\\Delta\\!\\!\\text{ }{{\\textit{H}}_{\\text{1}}}-\\!\\!\\Delta\\!\\!\\text{ }{{\\textit{H}}_{\\text{2}}}$ ； 无法判断

碳的摩尔燃烧焓是指$\rm 100\ Kpa$时，$\rm 1$ $\rm mol$碳完全燃烧生成$\rm CO_{2}(g)$时的焓变，即：目标化学方程式为$\text{C}\left( \text{s} \right)+{{\text{O}}_{\text{2}}}\left( \text{g} \right)\text{=C}{{\text{O}}_{\text{2}}}\left( \text{g} \right)$，利用盖斯定律，目标热化学方程式为$\text{C}\left( \text{s} \right)+{{\text{O}}_{\text{2}}}\left( \text{g} \right)\text{=C}{{\text{O}}_{\text{2}}}\left( \text{g} \right)$，可由$\rm 2\times $反应$\rm 4-$反应$\rm 1-$反应$\rm 2$得到，即$\Delta {{\textit{H}}_{5}}=\text{2 }\!\!\Delta\!\!\text{ }{{\textit{H}}_{\text{4}}}-\!\!\Delta\!\!\text{ }{{\textit{H}}_{\text{1}}}-\!\!\Delta\!\!\text{ }{{\textit{H}}_{\text{2}}}$；

$\rm CO(g)$的摩尔燃烧焓，反应$\rm 6$：$\text{CO}\left( \text{g}\right)+\dfrac{\text{1}}{\text{2}}\text{O}_{\text{2}}\left( \text{g}\right)\text{=C}\text{O}_{\text{2}}\left( \text{g}\right)\qquad\Delta\textit{H}_{6}$，$\rm H_{2}(g)$的摩尔燃烧焓，反应$\rm 7$：${{\text{H}}_{\text{2}}}\left( \text{g} \right)+\dfrac{\text{1}}{\text{2}}{{\text{O}}_{\text{2}}}\left( \text{g} \right)={{\text{H}}_{\text{2}}}\text{O}\left( \text{l} \right)$$\qquad\Delta H_{7}＜0$，反应$\rm 6-$反应$\rm 7$得：$\rm CO\left( \text{g}\right)+\text{H}_{2}\text{O}\left( \text{l}\right)\rightleftharpoons CO_{2}\left( \text{g}\right)+\text{H}_{2}\left( \text{g}\right)\qquad\Delta \textit{H}$，要比较$\rm CO(g)$的摩尔燃烧焓与$\rm H_{2}(g)$的摩尔燃烧焓的相对大小，即要求$\rm CO\left( \text{g}\right)+\text{H}_{2}\text{O}\left( \text{l}\right)\rightleftharpoons CO_{2}\left( \text{g}\right)+\text{H}_{2}\left( \text{g}\right)\qquad\Delta \textit{H}$与$\rm 0$的大小关系；反应$\rm 3-$反应$\rm 2$得反应$\rm 8$：$\rm CO\left( \text{g} \right)+{{\text{H}}_{2}}\text{O}\left( \text{g} \right)\rightleftharpoons C{{O}_{2}}\left( \text{g} \right)+{{\text{H}}_{2}}\left( \text{g} \right)\qquad\Delta {\textit{H}_{8}}=2.5.2-247.3=-42.1\;\rm kJ/mlol$，而过程$\rm 9$：$\rm H_{2}O(l)=$ $\rm H_{2}O(g)\qquad\Delta \textit{H}_{9}＞0$，反应$\rm 8+$过程$\rm 9$得：$\rm CO\left( \text{g}\right)+\text{H}_{2}\text{O}\left( \text{l}\right)\rightleftharpoons CO_{2}\left( \text{g}\right)+\text{H}_{2}\left( \text{g}\right)\qquad\Delta \textit{H}=\Delta \textit{H}_{8}+\Delta \textit{H}_{9}$，无法判断$\Delta {{H}_{8}}+\Delta {{H}_{9}}$大于$\rm 0$还是小于$\rm 0$ ，即无法判断$\rm CO(g)$的摩尔燃烧焓与$\rm H_{2}(g)$的摩尔燃烧焓的相对大小；

将$n\left( \text{C}{{\text{H}}_{4}} \right):n\left( \text{C}{{\text{O}}_{2}} \right)=1:1$的混合气体置于恒温恒压的密闭容器中，忽略反应$\rm 3$与反应$\rm 4$。测得充分反应后积碳产生量$\rm [C(s)$占体系中碳总量的摩尔分数$\rm ]$与温度、压强之间的关系如图。

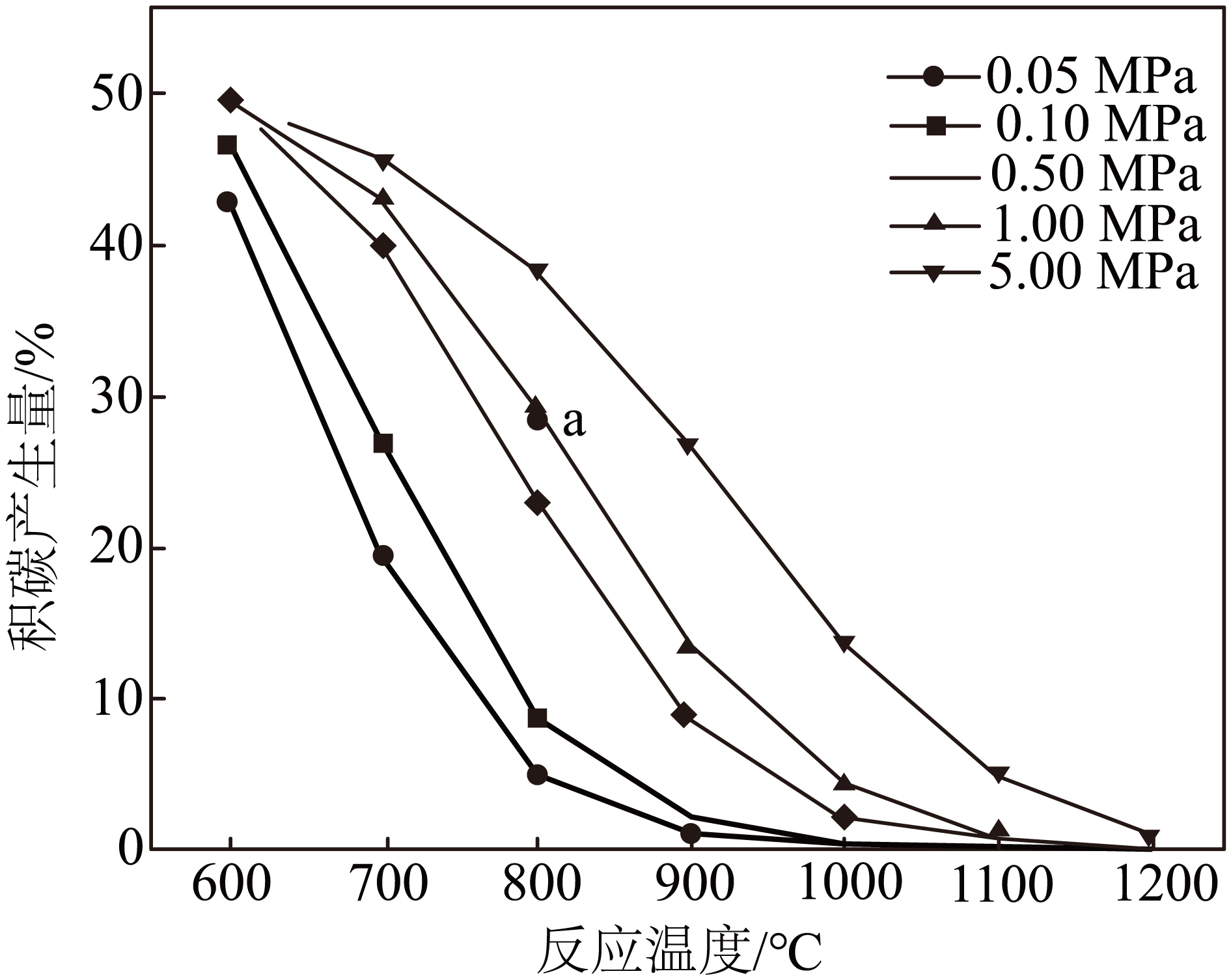
①温度升高会导致积碳减少或完全消失，原因为                。在$\rm a$点向容器中通入一定量${{\text{N}}_{2}}$，则积碳产生量会                $\rm ($填“增大”、“减少”或“不变”$\rm )$。

②在$T\ ^\circ\rm C$、$p\rm\ kPa$条件下，充分反应后，容器体积增加了$\rm 25\%$，反应$\rm 1$的压强平衡常数为$\dfrac{2p}{25}\ \text{kPa}$，则此时$\text{CO}$的分压为                $\rm \;\rm kPa$，反应$\rm 2$的压强平衡常数为${{K}_{\text{p}}}=$                $\rm kPa^{2}$。此时，下列能够促使反应$\rm 2$正向移动的有                $\rm ($填标号$\rm )$。

$\rm A$．加入少量$\text{C}\left( \text{s} \right)$      $\rm B$．升高温度      $\rm C$．加入合适催化剂      $\rm D$．以上均不可

随着温度升高，反应$\\rm 2$正向进行的程度更大 ； 减少 ；$0.2p$ ； $\\dfrac{4}{225}\\textit{p}^{\\text{2}}$； $\\rm AB$

①反应$\rm 1$和反应$\rm 2$均为吸热反应，升温，反应正方向进行程度增大，由于反应$\rm 2$正向进行的程度更大，甲烷减少，导致反应$\rm 1$逆移，故温度升高会导致积碳减少或完全消失；在$\rm a$点向容器中通入一定量$\rm N_{2}$，由于容器为恒温恒压容器，通入$\rm N_{2}$但总压不变，各组分分压减小，即等效减压，由图示可知，相同条件下，压强越小积碳产生量越少，所以在$\rm a$点向容器中通入一定量${{\text{N}}_{2}}$，积碳产生量减少；

②在$T\ ^\circ\rm C$、$p$ $\rm kPa$条件下，充分反应后，容器体积增加了$\rm 25\%$，反应$\rm 1$的压强平衡常数为$\dfrac{2p}{25}\ \text{kPa}$。设初始时 $n\rm(CH_{4})=\textit{n}(CO_{2})=1$ $\rm mol$，反应后气体总物质的量为 $\rm 2$ $\rm mol\times 125\%=2.5$ $\rm mol$。

假设反应$\rm 1$生成 $x$ $\rm mol$ $\rm C(s)$和 $2x$ $\rm mol$ $\rm H_{2}(g)$，反应$\rm 2$生成$2y$ $\rm mol$ $\rm CO(g)$和$2y\rm\ mol\ H_{2}(g)$ ，则平衡时$\rm CH_{4}$的物质的量为$1-x-y\rm\ mol$：

反应$\rm 1\begin{align} & \begin{matrix} {} & {} \\ \end{matrix}\begin{matrix} \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & {} \\ \end{matrix} & {} \\ \end{matrix}\text{C}{{\text{H}}_{4}}(\text{g})\rightleftharpoons \text{C}(\text{s})+2{{\text{H}}_{2}}(\text{g}) \\ &起始量 \text{mol}\begin{matrix} \begin{matrix} {} & {} & {} \\ \end{matrix} & {} & \begin{matrix} 0 & {} & 0 \\ \end{matrix} \\ \end{matrix} \\ & 变化量\text{mol}\begin{matrix} &\textit{x} & {} & \begin{matrix} {} & \textit{x} & \begin{matrix} {} & 2\textit{x} & {} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \\ &平衡量 \text{mol}\begin{matrix} {} & \begin{matrix} {} & {} \\ \end{matrix} & {} & \begin{matrix} \begin{matrix} \textit{x} & {} & 2\textit{x} \\ \end{matrix} & {} & {} \\ \end{matrix} \\ \end{matrix} \\ \end{align}$； 反应$\rm 2\begin{align} & \begin{matrix} {} & {} \\ \end{matrix}\begin{matrix} \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & {} \\ \end{matrix} & {} \\ \end{matrix}\text{C}{{\text{H}}_{\text{4}}}\text{(g)+C}{{\text{O}}_{\text{2}}}\text{(g)}\rightleftharpoons \text{2CO(g)+2}{{\text{H}}_{\text{2}}}\text{(g)} \\ & 起始量\text{mol}\begin{matrix} {} & {} & {} & {} \\ \end{matrix}\begin{matrix} 1 & {} & {} & {} \\ \end{matrix}\begin{matrix} 0 & {} & {} & 0 \\ \end{matrix} \\ & 变化量\text{mol}\begin{matrix} {} & \textit{y} & {} & {} \\ \end{matrix}\begin{matrix} \textit{y} & {} & {} & 2\textit{y} \\ \end{matrix}\begin{matrix} {} & {} & 2\textit{y} & {} \\ \end{matrix} \\ & 平衡量\text{mol}\begin{matrix} {} & \begin{matrix} {} & {} \\ \end{matrix} & 1-\textit{y} & {} \\ \end{matrix}\begin{matrix} {} & 2\textit{y} & {} & {} \\ \end{matrix}\begin{matrix} 2\textit{y} & {} & {} & {} \\ \end{matrix} \\ \end{align}$，平衡时气体的总物质的量为①$1-x-y+1-y+2x+2y+2y=2.5\;\rm mol$：反应$\rm 1$的$\textit{K}_{\text{p}}=\dfrac{\textit{p}^{\text{2}}\left( \text{H}_{\text{2}}\right)}{\textit{p}\left( \text{C}\text{H}_{\text{4}}\right)}=\dfrac{\left( \dfrac{2\textit{x}+2\textit{y}}{2.5}\textit{p}\right)^{2}}{\dfrac{1-\textit{x}-\textit{y}}{2.5}\textit{p}}=\dfrac{2\textit{p}}{\text{25}}\ \text{kPa}$，假设总压为 $p$ $\rm kPa$ ，则：$\textit{p}\left( \text{C}{{\text{H}}_{\text{4}}} \right)=\dfrac{\textit{n}\left( \text{C}{{\text{H}}_{\text{4}}} \right)}{{\textit{n}_{总}}}\textit{p}=\dfrac{1-x-y}{2.5}\textit{p}$，$\textit{p}\left( {{\text{H}}_{\text{2}}} \right)=\dfrac{\textit{n}\left( {{\text{H}}_{2}} \right)}{{\textit{n}_{总}}}\textit{p}=\dfrac{2x+2y}{2.5}\textit{p}$， 代入平衡常数表达式：②$\dfrac{\left( \dfrac{2x+2y}{2.5}\textit{p}\right)^{2}}{\dfrac{1-x-y}{2.5}\textit{p}}=\dfrac{2\textit{p}}{\text{25}}\ \text{kPa}$，联立①②解得：$x=-0.1$，$y=0.3$，起始并没有加碳，$x$不可能小于$\rm 0$，因此该条件下，反应$\rm 1$未进行，反应后气体物质的量增加$\rm 0.5\;\rm mol$，则有$2y=0.5$，$\textit{p}\left( \text{CO} \right)=\dfrac{n\left( \text{CO} \right)}{{{n}_{总}}}\textit{p}=\dfrac{2y}{2.5}\textit{p}=\dfrac{0.5}{2.5}\textit{p}=0.2\textit{p}\rm\ kPa$，所以反应$\rm 2$的压强平衡常数为：$\textit{K}_{\text{p}}=\dfrac{\textit{p}^{\text{2}}\left( \text{CO}\right)\textit{p}^{\text{2}}\left( \text{H}_{\text{2}}\right)}{\textit{p}\left( \text{C}\text{H}_{\text{4}}\right)\textit{p}\left( \text{C}\text{O}_{\text{2}}\right)}=\dfrac{\left( 0.2\textit{p}\right)^{2}\times\left( 0.2\textit{p}\right)^{2}}{\left( \dfrac{1-0.25}{2.5}\textit{p}\right)\times\left( \dfrac{1-0.25}{2.5}\textit{p}\right)}=\dfrac{4\textit{p}^{2}}{225}\ \text{kPa}$；

$\rm A$．最初没有加碳，此时加碳，对反应$\rm 1$，$\textit{Q}=\dfrac{\textit{p}^{2}\left( \text{H}_{2}\right)}{\textit{p}\left(\rm CH_{4}\right)}=\sqrt{\textit{K}_{\text{p}2}}=\sqrt{\dfrac{4\textit{p}^{2}}{225}}\rm kPa=\dfrac{2\textit{p}}{15}kPa\gt\dfrac{2\textit{p}}{25}kPa=\textit{K}_{\text{p}1}$，反应$\rm 1$逆向进行，甲烷物质的量增多，反应$\rm 2$正向移动，$\rm A$正确；

$\rm B$．因为反应$\rm 2$为吸热反应，升高温度有利于正向移动，$\rm B$正确；

$\rm C$．催化剂可以加快反应速率，但不改变平衡，$\rm C$错误；

$\rm D$．由以上分析可知，$\rm A$、$\rm B$正确，$\rm D$错误；

故选：$\rm AB$