高中 | 化学平衡常数 题目答案及解析
稿件来源:高途
高中 | 化学平衡常数题目答案及解析如下,仅供参考!
选修四
第二章 化学反应速率和化学平衡
第三节 化学平衡
化学平衡常数
$\rm TiCl_{4}$用于制备海绵钛和钛白粉。一定条件下,可利用金红石$\rm (TiO_{2})$、$\rm C$和$\rm Cl_{2}$反应制得,涉及主要反应如下:
Ⅰ.$\rm TiO_{2}(s)+2Cl_{2}(g)+2C(s)\rightleftharpoons \rm TiCl_{4}(g)+2CO(g)$ $\qquad\Delta H_{1}=-49\;\rm kJ/mol$
Ⅱ.$\rm TiO_{2}(s)+2Cl_{2}(g)+C(s)\rightleftharpoons \rm TiCl_{4}(g)+CO_{2}(g)$ $\qquad\Delta H_{2}=-222\;\rm kJ/mol$
Ⅲ.$\rm C(s)+CO_{2}(g)\rightleftharpoons \rm 2CO(g)$ $\qquad\Delta H_{3}$
回答下列问题:
$\Delta H_{3}=$ $\rm \;\rm kJ/mol$。
$\\rm +173$
"]]根据盖斯定律,反应Ⅲ$\rm =$反应Ⅰ$\rm -$反应Ⅱ,$\Delta H_{3}=-49\;\rm kJ/mol+222\;\rm kJ/mol=+173$ $\rm kJ/mol$;
若在$\rm 100\;\rm kPa$下,足量的$\rm TiO_{2}$、$\rm C$和$\rm Cl_{2}$发生上述反应,达到平衡后,气相中$\rm TiCl_{4}$、$\rm CO$和 $\rm CO_{2}$摩尔分数随温度的变化关系如图所示。
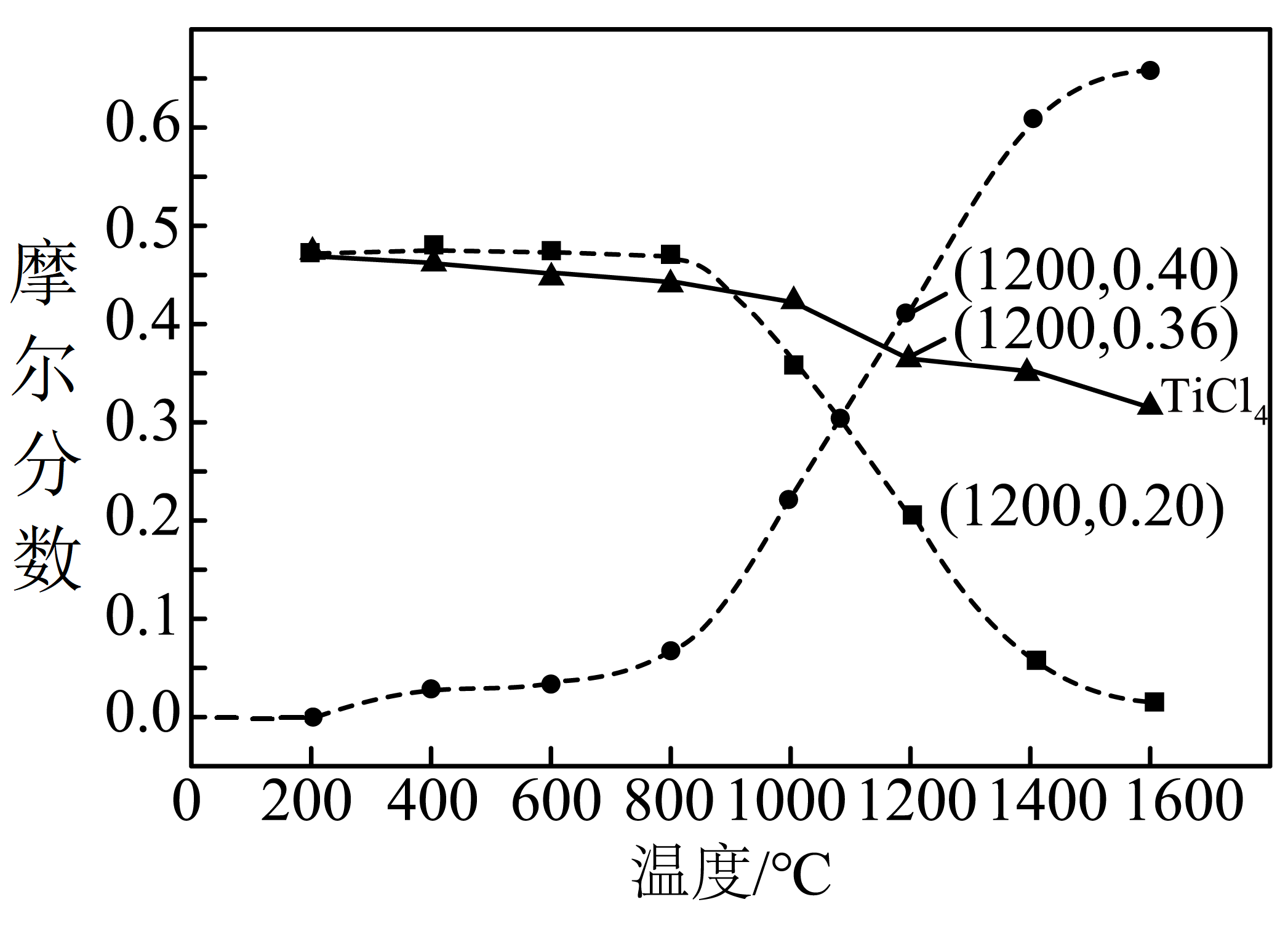
结合上图分析,实际生产中反应温度选择$\rm 800-1000\;\rm ^\circ\rm C$的原因是 。$\rm 200\;\rm ^\circ\rm C$时,若向平衡体系中通入少量$\rm Cl_{2}$,$\rm TiO_{2}$氯化反应的化学平衡将 $\rm ($填“正向移动”、“逆向移动”或“不移动”$\rm )$,$\rm Cl_{2}$的平衡转化率 $\rm ($填“增大”、“减小”或“不变”$\rm )$。$\rm 1200\;\rm ^\circ\rm C$时,反应Ⅰ的平衡常数$K\rm_p=$ $\rm \;\rm kPa$。
温度低于$\\rm 800\\;\\rm ^\\circ\\rm C$,反应速率慢,高于$\\rm 1000\\;\\rm ^\\circ\\rm C$,$\\rm TiCl_{4}$的摩尔分数显著降低; 正向移动 ; 不变 ; $\\rm 3600$
"]]反应Ⅰ、Ⅱ均为放热反应,升高温度,平衡逆向移动,反应Ⅲ吸热,升温,$\rm CO$增多,$\rm CO_{2}$减少;实际生产中反应温度选择$\rm 800-1000\;\rm ^\circ\rm C$的原因是:其它条件不变时,温度低于$\rm 800\;\rm ^\circ\rm C$,反应速率慢,高于$\rm 1000\;\rm ^\circ\rm C$,$\rm TiCl_{4}$的摩尔分数显著降低;$\rm 200\;\rm ^\circ\rm C$时,$\rm CO$的摩尔分数为$\rm 0$,说明只发生了反应Ⅱ,若向平衡体系中通入少量$\rm Cl_{2}$,$\rm TiO_{2}$氯化反应的反应物浓度增大,化学平衡将正向移动,通入少量$\rm Cl_{2}$,压强增大,由于反应Ⅱ为等体积反应,反应物中气体只有$\rm Cl_{2}$,$\rm Cl_{2}$自身的平衡转化率不变;根据图示,$\rm 1200\;\rm ^\circ\rm C$时,$\rm TiCl_{4}$的摩尔分数为$\rm 0.36$,$\rm CO$的摩尔分数为$\rm 0.40$,$\rm CO_{2}$的摩尔分数为$\rm 0.20$,则$\rm Cl_{2}$的摩尔分数为$\rm 0.04$,反应Ⅰ的平衡常数$K\rm_p=\dfrac{\textit{P}^{2}\text{(CO)}\cdot\textit{P}\text{(TiCl}_{4}\text{)}}{\textit{P}^{2}\text{(C}\text{l}_{2}\text{)}}=\dfrac{40^{2}\times36}{4^{2}}=3600$;
一定条件下,若向$\rm 15\;\rm L$恒容容器中加入$\rm 5\;\rm mol$ $\rm TiO_{2}$与$\rm 15\;\rm mol$碳粉,通入$\rm 10\;\rm mol$ $\rm Cl_{2}$发生上述反应,不同时间测得混合体系内各物理量见下表:
| $t/\rm\min$ | $\rm 10$ | $\rm 20$ | $\rm 30$ | $\rm 40$ |
| $n\rm(Cl_{2})/mol$ | $\rm 6$ | $\rm 2.5$ | $\rm 1$ | $\rm 1$ |
| $n\rm(C)/mol$ | $\rm 12$ | $\rm 10$ | $\rm 9$ | $\rm 9$ |
| $p\rm(CO)$:$p\rm(CO_{2})$ | $\rm 2$:$\rm 1$ | $\rm 1$:$\rm 1$ | $\rm 1$:$\rm 1$ | $\rm 1$:$\rm 1$ |
已知起始总压强为$\rm 6\ MPa$,$\rm 10\;\rm min$时,体系总压强为 ;$\rm 0-20\;\rm min$内,用$\rm TiCl_{4}$压强变化表示的化学反应速率$v=$ $\rm MPa/min$。
$\\rm 6.6\\ MPa$ ; $\\rm 0.1125$
"]]根据碳原子守恒,$\rm 10\;\rm min$时消耗$\rm 3\;\rm mol\;\rm C$,生成$\rm CO$和 $\rm CO_{2}$共$\rm 3\;\rm mol$,消耗$\rm 4\;\rm mol$ $\rm Cl_{2}$,生成$\rm TiCl_{4}\ 2\;\rm mol$,平衡时气体总的物质的量为$\rm 6\;\rm mol+3\;\rm mol+2\;\rm mol=11\;\rm mol$,恒温恒容,气体压强之比等于其物质的量之比,可知$\rm 10\;\rm min$时,体系总压强为$\dfrac{11\;\rm \text{mol}}{10\;\rm \text{mol}}\times 6\ \text{MPa}\rm =6.6\ MPa$;$\rm 20\;\rm min$时消耗$\rm 5\;\rm mol\;\rm C$,生成$\rm CO$和 $\rm CO_{2}$共$\rm 5\;\rm mol$,消耗$\rm 7.5\;\rm mol$ $\rm Cl_{2}$,生成$\rm TiCl_{4}\ 3.75\;\rm mol$,平衡时气体总的物质的量为$\rm 2.5\;\rm mol+5\;\rm mol+3.75\;\rm mol=11.25\;\rm mol$,恒温恒容,气体压强之比等于其物质的量之比,可知$\rm 20\;\rm min$时,体系总压强为$\dfrac{11.25\;\rm \text{mol}}{10\;\rm \text{mol}}\times 6\ \text{MPa}\rm =6.75\ MPa$,$\rm TiCl_{4}$分压为$\dfrac{3.75\;\rm \text{mol}}{11.25\;\rm \text{mol}}\times 6.75\ \text{MPa}\rm =2.25\ MPa$,用$\rm TiCl_{4}$压强变化表示的化学反应速率$v=\dfrac{2.25\ \text{MPa}}{20\;\rm \min }=\rm 0.1125\ MPa/min$。
高中 | 化学平衡常数题目答案及解析(完整版)
