高中 | 化学平衡常数 题目答案及解析
稿件来源:高途
高中 | 化学平衡常数题目答案及解析如下,仅供参考!
选修四
第二章 化学反应速率和化学平衡
第三节 化学平衡
化学平衡常数
近日,石河子大学于锋教授团队制备了钙镁铝复合氧化物$\rm (P-CaMgAl-LDO)$,该材料具有优异的$\rm CO_{2}$吸附性能,有利于$\rm CO_{2}$催化加氢制备$\rm CH_{3}OH$,涉及如下反应。
Ⅰ.${\rm CO_{2}(g)+3H_{2}(g)\rightleftharpoons CHOH(g)+H_{2}O(g)}\quad\Delta H_{1}$
Ⅱ.${\rm CO_{2}(g)+H_{2}(g)\rightleftharpoons CO(g)+H_{2}O(g)}\quad\Delta H_{2}=+41.1\rm \ kJ\cdot mol^{-1}$
Ⅲ.${\rm CO(g)+2H_{2}(g)\rightleftharpoons CH_{3}OH(g)}\quad\Delta H_{3}=-90.4\rm \ kJ\cdot mol^{-1}$
回答下列问题:
基态$\rm Mg$原子中$\rm s$、$\rm p$能级上电子总数之比为 。
$\\rm 1:1$
"]]基态$\rm Mg$原子核外电子排布式为$\rm 1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}$,则基态$\rm Mg$原子中$\rm s$、$\rm p$能级上电子总数之比为$\rm 6:6=1:1$。
高温下$\rm CaO$与焦炭反应生成$\rm CaC_{2}$,反应为$\rm CaO+3C\begin{matrix} \underline{\underline{高温}} \\ {} \\ \end{matrix}CaC_{2}+CO↑$,四方晶系$\rm CaC_{2}$的晶胞结构如图所示。
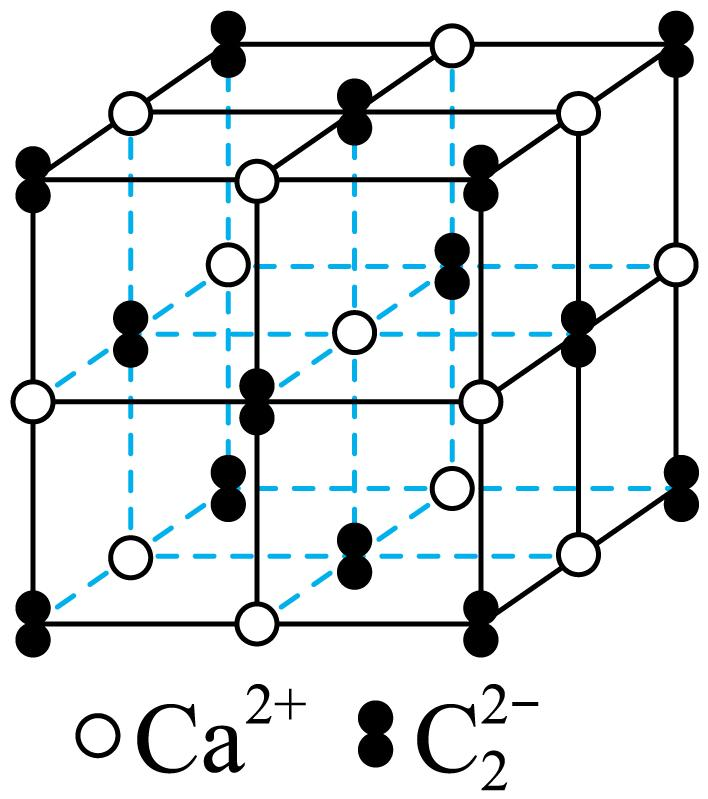
①$\rm CaC_{2}$中$\rm \sigma$键、$\rm \pi$键的数目之比为 。
②已知$\rm CaC_{2}$的晶胞与$\rm NaCl$的晶胞类似,晶胞参数$a\ {\rm nm}=b\ {\rm nm}≠c\ \rm nm$,设$N_{\rm A}$为阿伏加德罗常数的值,该晶体的密度为 $\rm \ g\cdot cm^{-3}($用含$a$,$b$、$c$和$N_{\rm A}$的代数式表示$\rm )$。
$\\rm 1:2$;$\\dfrac{2.56\\times 1{{0}^{23}}}{abc{{N}_{\\rm A}}}$
"]]①$\rm Ca{{C}_{2}}$由$\rm C{{a}^{2+}}$和$\rm C_{2}^{2-}$构成,$\rm C_{2}^{2-}$中含有一个$\rm \sigma$键,两个$\rm \pi $键,则$\rm Ca{{C}_{2}}$中$\rm \sigma$键、$\rm \pi$键的数目之比为$\rm 1:2$。
②根据晶胞结构可知,该晶胞中含有$\rm 12\times \dfrac{1}{4}+1=4$个$\rm C{{a}^{2+}}$,$\rm 8\times \dfrac{1}{8}+6\times \dfrac{1}{2}=4$个$\rm C_{2}^{2-}$,则该晶体的密度$\rho=\dfrac{N\times M}{{{N}_{\rm A}}\times V}=\dfrac{4\times (40+24)}{abc{{N}_{\rm A}}\times {{10}^{-21}}}=\dfrac{2.56\times {{10}^{23}}}{abc{{N}_{\rm A}}}\ \rm g\cdot cm^{-3}$。
反应的$\Delta H_{1}=$ $\rm kJ\cdot mol^{-1}$。
$-49.3$
"]]根据盖斯定律可知,反应I=反应II+反应III,则$\Delta{{H}_{1}}=\Delta {{H}_{2}}+\Delta {{H}_{3}}=+41.1-90.4=-49.3\rm \ kJ/mol$。
在体积可变的密闭容器中以$\rm CO$和$\rm H_{2}$物质的量之比$1:3$充入混合气体发生上述反应,测得$\rm CO_{2}$平衡转化率与温度﹑压强的关系如图所示。
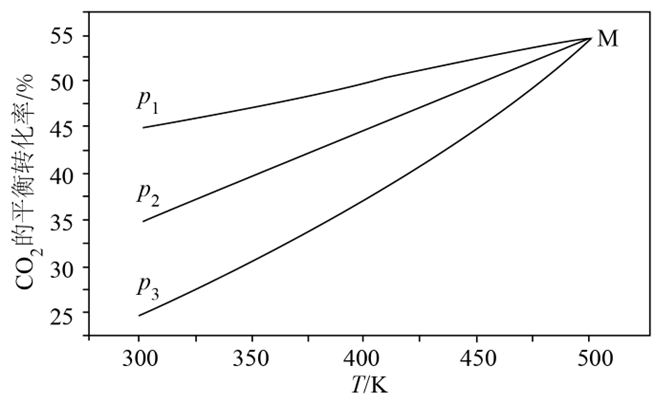
①根据图像,$p_{1}$、$p_{2}$、$p_{3}$由大到小的顺序为 ,判断依据是 。
②随着温度升高,不同压强下,$\rm CO_{2}$平衡转化率趋向交于M点,可能的原因是 。
$p_{1}\\gt p_{2}\\gt p_{3}$;反应Ⅰ、Ⅲ是气体分子数减小的反应,反应Ⅱ是气体分子数不变的反应,其他条件相同,增大压强,$\\rm CO_{2}$平衡转化率增大;随着温度升高,逐渐以反应Ⅱ为主,压强对平衡的影响逐渐减小,平衡转化率主要由温度决定
"]]①在温度相同的情况下,反应Ⅰ、Ⅲ是气体分子数减小的反应,反应Ⅱ是气体分子数不变的反应,${{p}_{1}}$至${{p}_{3}}$过程中,$\rm C{{O}_{2}}$平衡转化率减小,说明平衡逆向移动,减小压强,平衡向气体分子数增大的方向移动,即逆向移动,故${{p}_{1}}\gt {{p}_{2}}\gt {{p}_{3}}$;判断依据是:反应Ⅰ、Ⅲ是气体分子数减小的反应,反应Ⅱ是气体分子数不变的反应,其他条件相同,增大压强,$\rm C{{O}_{2}}$平衡转化率增大。
②反应$\rm I$、$\rm III$为放热反应,反应$\rm I$为吸热反应,随着温度升高,逐渐以反应Ⅱ为主,同时反应Ⅱ是气体分子数不变的反应,压强对平衡的影响逐渐减小,平衡转化率主要由温度决定,所以$\rm C{{O}_{2}}$平衡转化率趋向交于$\rm M$点的原因可能是:随着温度升高,逐渐以反应Ⅱ为主,压强对平衡的影响逐渐减小,平衡转化率主要由温度决定。
一定条件下,向体积为$\rm 2\ L$的恒容密闭容器中通入$\rm 1\ mol\ CO_{2}$和$\rm 3\ mol\ H_{2}$,发生上述反应,达到平衡时,容器中$\rm CH_{3}OH(g)$为$\rm 0.4\ mol$,$\rm CO$为$\rm 0.2\ mol$,此时,$\rm H_{2}O(g)$的浓度为 $\rm \ mol\cdot L^{-1}$,反应$\rm II$的物质的量分数平衡常数$K_{\rm x}=$ $(K_{\rm x}$为用物质的量分数替代浓度计算的平衡常数$\rm )$。
$0.3$;$\\dfrac{3}{16}$或$0.1875$
"]]假设反应$\rm I$消耗$x\ \rm mol\ C{{O}_{2}}$,反应$\rm II$消耗$y\ \rm mol\ C{{O}_{2}}$,根据信息可建立关系式,反应$\rm I$:$\rm \begin{matrix} {} & \rm C{{O}_{2}}(g) & + & \rm 3{{H}_{2}}(g) & \rightleftharpoons & \rm C{{H}_{3}}OH(g) & + & \rm {{H}_{2}}O(g) \\ 转化\rm /mol & x & {} & 3x & {} & x & {} & x \\ \end{matrix}$,反应$\rm II$:$\rm \begin{matrix} {} & \rm C{{O}_{2}}(g) & + & \rm {{H}_{2}}(g) & \rightleftharpoons & \rm CO(g) & + & \rm {{H}_{2}}O(g) \\ 转化\rm /mol & y & {} & y & {} & y & {} & y \\ \end{matrix}$,反应$\rm III$:$\rm \begin{matrix} {} & \rm CO(g) & + & \rm 2{{H}_{2}}(g) & \rightleftharpoons & \rm C{{H}_{3}}OH(g) \\ 转化\rm /mol & 0.4-x & {} & 0.8-2x & {} & 0.4-x \\ \end{matrix}$,$n{\rm (CO)}=y-0.4+x=0.2$,则$n{\rm ({{H}_{2}}O)}=x+y=0.6\rm \ mol$,$c{\rm ({{H}_{2}}O)}=\rm \dfrac{0.6\ mol}{2\ L}=0.3\ mol/L$;平衡时,$n{\rm ({{H}_{2}}O)}=0.6\rm \ mol$,$n{\rm (CO)}=0.2\rm \ mol$,$n{\rm (C{{O}_{2}})}=1-(x+y)=0.4\rm \ mol$,$n{\rm ({{H}_{2}})}=3-(3x+y+0.8-2x)=1.6\rm \ mol$,则${{K}_{\rm x}}=\dfrac{\dfrac{0.6}{3.2}\times \dfrac{0.2}{3.2}}{\dfrac{0.4}{3.2}\times \dfrac{1.6}{3.2}}=\dfrac{3}{16}$。
高中 | 化学平衡常数题目答案及解析(完整版)
