天然水中可以分离出重水$\rm (D_{2}O)$。$\rm D_{2}O$溶液中存在电离平衡：${{\text{D}}_{2}}\text{O}\rightleftharpoons {{\text{D}}^{+}}+\text{O}{{\text{D}}^{-}}$，$c\rm (D^{+})$和$c(\rm OD^{-})$的关系如图所示。

①图中$\rm 3$个状态点对应的溶液呈中性的是                。

②${{ {T}}_{1}}$                ${{ {T}}_{2}}\rm ($填“$\rm \gt $”“$\rm =$”或者“$\rm \lt $”$\rm )$。

$\\rm B$；$\\rm \\gt $

①重水中存在电离平衡$\rm {{{D}}_{2}}{O}\rightleftharpoons {{{D}}^{-}}+{O}{{{D}}^{-}}$，中性溶液中，${c(}{{{\rm D}}^{-}})={c}\rm ({O}{{{D}}^{-}})$，只有$\rm B$点符合，所以“$\rm A$、$\rm B$、$\rm C$”三点中呈中性的是$\rm B$点；

②水的电离平衡为吸热过程，温度升高，电离程度增大，${c(}{\rm {{D}}^{-}})$，${c}(\rm {O}{{{D}}^{-}})$均增大，$ K_\rm w$也增大，由图可知，$ T_{1}$时离子浓度更高，$ K_\rm w$更大，所以${{{T}}_{1}} \gt {{{T}}_{2}}$；

用如图所示电化学装置进行如下实验。

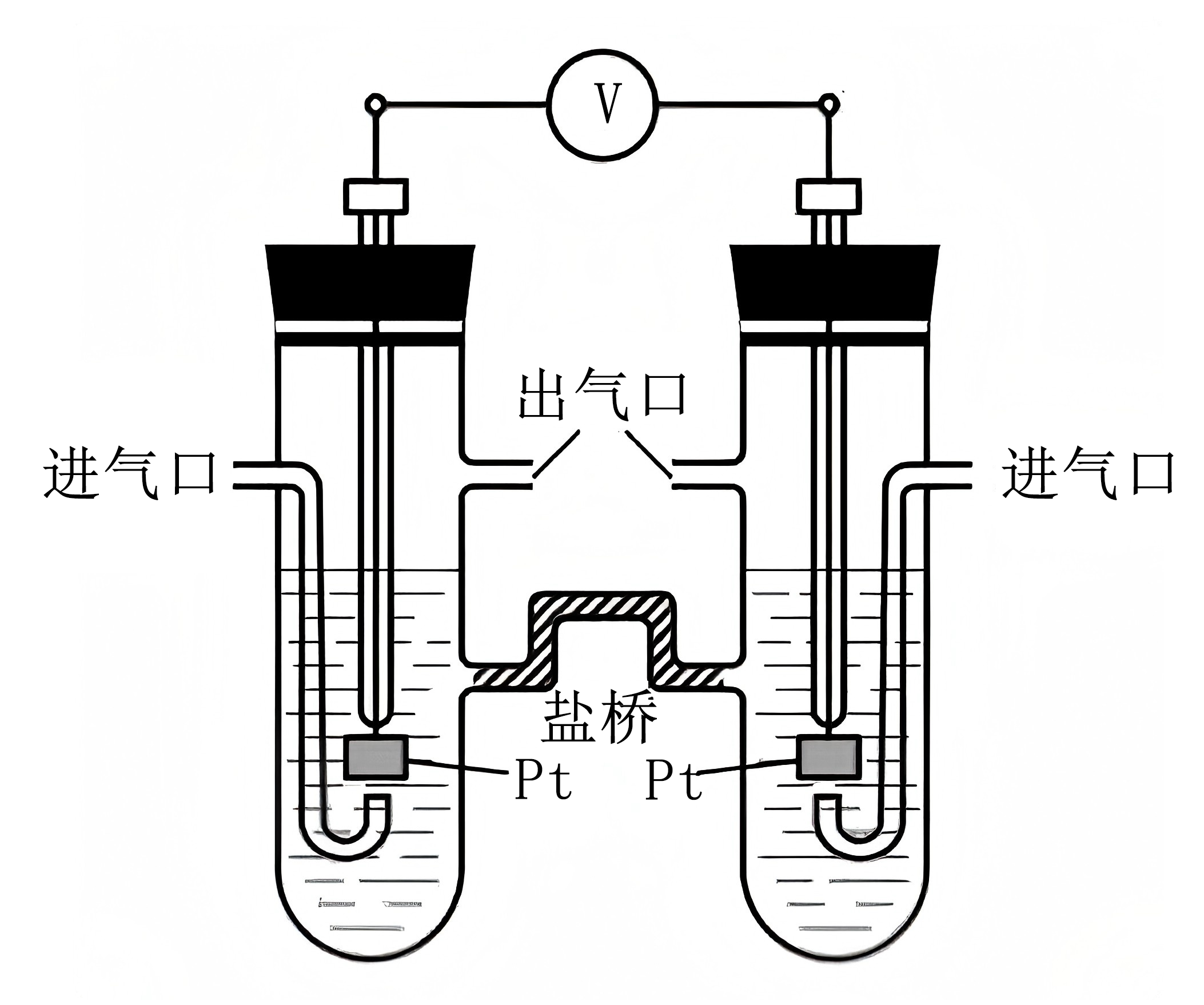
①用${{\text{H}}_{2}}$实验：在左侧通入${{\text{H}}_{2}}$，产物为${{\text{H}}_{2}}\text{O}$，盐桥中${{\text{K}}^{+}}$移向装置的                $\rm ($填“左侧”或者“右侧”$\rm )$，电池的总反应为                。

②用${{\text{O}}_{2}}$实验：在一侧通入${{\text{O}}_{2}}$，电池的总反应仍保持不变，该侧的电极反应为                。

右侧；$\\text{2}{{\\text{H}}_{\\text{2}}}+{{\\text{O}}_{\\text{2}}}=2{{\\text{H}}_{2}}\\text{O}$；${{\\text{O}}_{2}}+4{{\\text{e}}^{-}}+2{{\\text{H}}_{2}}\\text{O}=4\\text{O}{{\\text{H}}^{-}}$

①用${{\text{H}}_{2}}$进行实验，左侧通入${{\text{H}}_{2}}$，产物为${{\text{H}}_{2}}\text{O}$，电极方程式为：${{\text{H}}_{\text{2}}}\text{-2}{{\text{e}}^{-}}\text{+2O}{{\text{H}}^{-}}\text{=2}{{\text{H}}_{\text{2}}}\text{O}$，左侧为负极，右侧为正极，电极方程式为${{\text{O}}_{2}}+4{{\text{e}}^{-}}+2{{\text{H}}_{2}}\text{O}=4\text{O}{{\text{H}}^{-}}$，在原电池中，正电荷向正极移动，所以盐桥中${{\text{K}}^{+}}$移向正极，即右侧，该电池为燃料电池，原料为氢气和氧气，总反应方程式为$\text{2}{{\text{H}}_{\text{2}}}+{{\text{O}}_{\text{2}}}=2{{\text{H}}_{2}}\text{O}$；

②用${{\text{O}}_{2}}$进行实验，一侧通入${{\text{O}}_{2}}$，电池总反应方程式不变，则该电池为氢气和氧气组成的燃料电池，该侧的电极反应方程式为${{\text{O}}_{2}}+4{{\text{e}}^{-}}+2{{\text{H}}_{2}}\text{O}=4\text{O}{{\text{H}}^{-}}$；

利用驰豫法可研究快速反应的速率常数$(k$，在一定温度下为常数$\rm )$。其原理是通过微扰$\rm ($如瞬时升温$\rm )$使化学平衡发生偏离，观测体系微扰后从不平衡态趋向新平衡态所需的驰豫时间$\rm ({ }\tau{ }\rm )$，从而获得$k$的信息。对于$\rm {{{H}}_{2}}{O}\rightleftharpoons {{{H}}^{+}}+{O}{{{H}}^{-}}$，若将纯水瞬时升温到$\rm 25\;\rm ^\circ\rm C$，测得${ }\tau=4.0\times {{10}^{-5}}\rm \;{s}$。已知：$\rm 25\;\rm ^\circ\rm C$时，${c}\left(\rm {{{H}}_{2}}{O} \right)=55.6\;\rm {mol}/{L}$，${v}\left(\rm正 \right)={{{k}}_{1}}{c}\left(\rm {{{H}}_{2}}{O} \right)$，${v}\left(\rm逆 \right)={{{k}}_{2}}{c}\left(\rm {{{H}}^{+}} \right){c}\left(\rm {O}{{{H}}^{-}} \right)$，$\tau{ }=\dfrac{1}{{{{k}}_{1}}+2{{{k}}_{2}}{{{x}}_{\rm {e}}}} ({{x}_{\rm {e}}}$为$\rm {{{H}}^{+}}$的平衡浓度$\rm )$。

①$\rm 25\;\rm ^\circ\rm C$时，$\rm {{{H}}_{2}}{O}\rightleftharpoons {{{H}}^{+}}+{O}{{{H}}^{-}}$的平衡常数${K}=$                $\;\rm {mol}/{L}\rm ($保留$\rm 2$位有效数字$\rm )$。

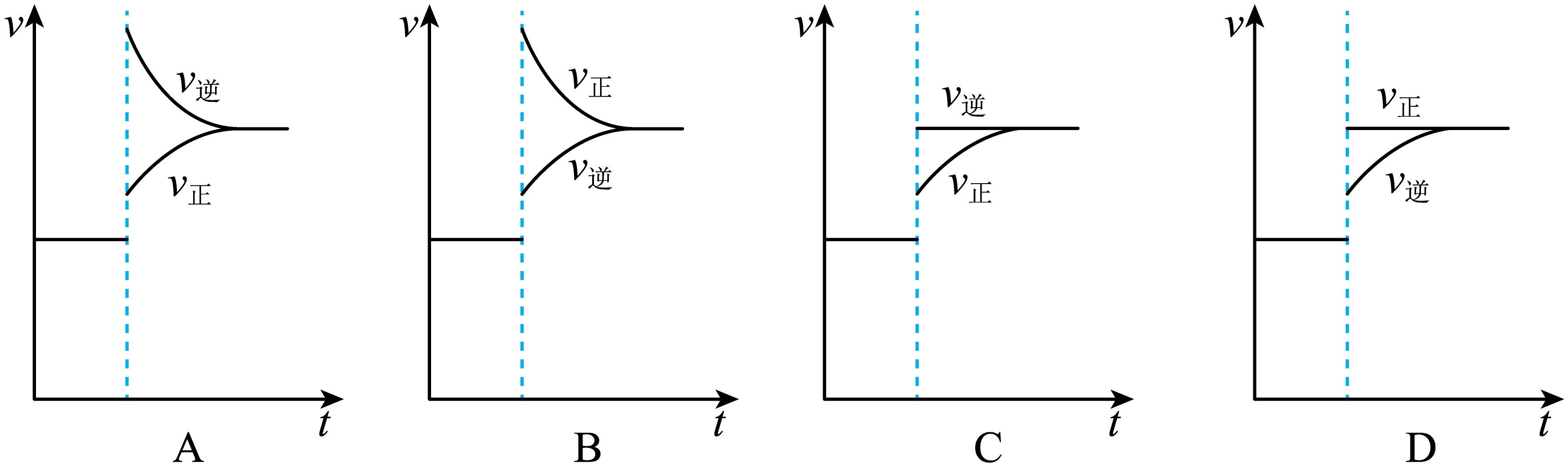
②下列能正确表示瞬时升温后反应建立新平衡的过程示意图为                。

③$\rm 25\;\rm ^\circ\rm C$时，计算得${{ {k}}_{2}}$为                $\text{L}/\left( \text{mol}\cdot \text{s} \right)$。

${K}=1.8\\times {{10}^{-16}}$；$\\rm D$；${{{k}}_{2}}=1.25\\times {{10}^{11}}$

①对于反应$\rm {{{H}}_{2}}{O}\rightleftharpoons {{{H}}^{+}}+{O}{{{H}}^{-}}$，平衡常数$ K$的定义为：$ K=\dfrac{c\left(\rm {{{H}}^{+}} \right){c}\left(\rm {O}{{{H}}^{-}} \right)}{{c}\left(\rm {{{H}}_{2}}{O} \right)}$，在$\rm 25\;\rm ^\circ\rm C$的纯水中，水的离子积常数为$ K_{\rm w}={c}\left(\rm {{{H}}^{+}} \right){c}\left(\rm {O}{{{H}}^{-}} \right)=1\times {{10}^{-14}}$，而且平衡时${c}\left(\rm {{{H}}^{+}} \right){=c}\left(\rm {O}{{{H}}^{-}} \right)=1\times {{10}^{-7}}$，已知${c}\left(\rm {{{H}}_{2}}{O} \right)=55.6\;\rm {mol}/{L}$，带入公式：$ K=\dfrac{1\times {{10}^{-7}}{{}^{2}}}{55.6}=\dfrac{{{10}^{-14}}}{55.6}\approx 1.798\times {{10}^{-16}}$，保留两位小数$ K=1.8\times {{10}^{-16}}$；

②瞬时升温后，逆反应速率增大，但水的浓度是恒定的，正反应速率不变，所以建立新平衡的过程示意图为$\rm D$，

③驰豫时间公式为$\tau=\dfrac{1}{{{{k}}_{1}}+2{{{k}}_{2}}{{{x}}_{\rm {e}}}}$，其中$\tau=4.0\times {{10}^{-5}}\rm \;{s}$，${{{x}}_{\rm {e}}}{=c}\left(\rm {{{H}}^{+}} \right)=1\times {{10}^{-7}}$，带入得：${{{k}}_{1}}+2{{{k}}_{2}}\times {(1}\times {1}{{{0}}^{{-7}}}{)}=\dfrac{1}{\tau}=\dfrac{1}{4\times {1}{{{0}}^{{-5}}}}=2.5\times {1}{{{0}}^{{4}}}\rm \;{{{s}}^{{-1}}}$，在平衡时，${v}\left(\rm正 \right)={v}\left(\rm逆 \right)$，可推出${{{k}}_{1}}{c}\left(\rm {{{H}}_{2}}{O} \right)={{{k}}_{2}}{c}\left(\rm {{{H}}^{+}} \right){c}\left(\rm {O}{{{H}}^{-}} \right)={{{k}}_{2}}{x}_{\rm {e}}^{{2}}$，带入已知值：${{{k}}_{1}}\times 55.6={{{k}}_{2}}\times {{(1\times {{10}^{-7}})}^{2}}$，即${{{k}}_{1}}=\dfrac{{{{k}}_{2}}\times {{10}^{-14}}}{55.6}$，将$k_{1}$带入驰豫时间公式为：$\dfrac{{{{k}}_{2}}\times {{10}^{-14}}}{55.6}{+2}{{{k}}_{2}}\times 1\times {{10}^{-7}}=2.5\times {{10}^{4}}$，整理可得，${{{k}}_{2}}(\dfrac{{{10}^{-14}}}{55.6}{+2}\times {{10}^{-7}})=2.5\times {{10}^{4}}$，计算括号内：$\dfrac{{{10}^{-14}}}{55.6}\approx 1.80\times {{10}^{-16}}$，${2}\times {{10}^{-7}}=2.00\times {{10}^{-7}}$，由于$1.80\times {{10}^{-16}}\ll 2.00\times {{10}^{-7}}$，可忽略不计，所以${{{k}}_{2}}\times 2\times {{10}^{-7}}=2.5\times {{10}^{4}}$，得出${{{k}}_{2}}=1.25\times {{10}^{11}}\rm \;{L}/\left(\rm {mol}\cdot {s} \right)$。