反应Ⅰ、Ⅱ、Ⅲ的焓变$\Delta H$随温度$ {T}$的变化如图$\rm 1$所示。表示反应Ⅰ的焓变曲线为                $\rm ($填“$\rm a$”“$\rm b$”或“$\rm c$”$\rm )$，反应Ⅲ在                $\rm ($填“高温”“低温”或“任何温度”$\rm )$下可自发进行。

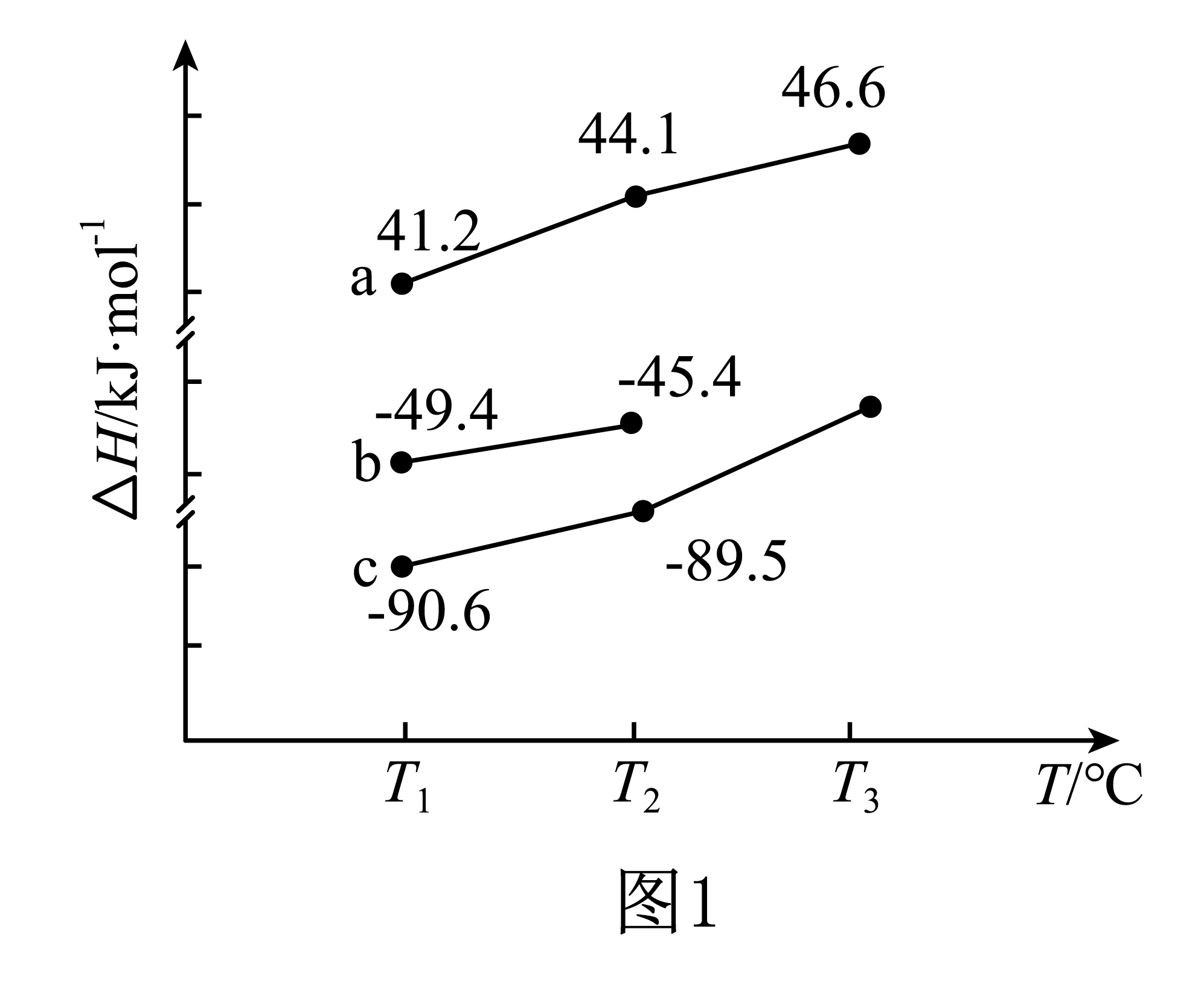
$\\rm b$；低温

依据盖斯定律Ⅰ$\rm -$Ⅱ可得Ⅲ，只有反应$\rm II$的$\Delta H_{2}\gt 0$，则曲线$\rm a$代表$\rm II$，将$ T_{1}$时各曲线数据代入$\rm -49.4-41.2=-90.6$，则曲线$\rm b$代表$\rm I$，曲线$\rm c$代表$\rm III$；反应$\rm III$是气体分子数减小的反应，则$\Delta S\lt 0$，已知$\Delta H_{3}\lt 0$，故低温时，$\Delta H-T\Delta S\lt 0$反应自发；

在恒容密闭容器中按$ {n}\left( \text{C}{{\text{O}}_{2}} \right):{n}\left( {{\text{H}}_{2}} \right)\rm =1: 3$投料进行上述反应，$\text{C}{{\text{O}}_{2}}$的平衡转化率和甲醇的选择性随温度的变化趋势如图$\rm 2$所示：

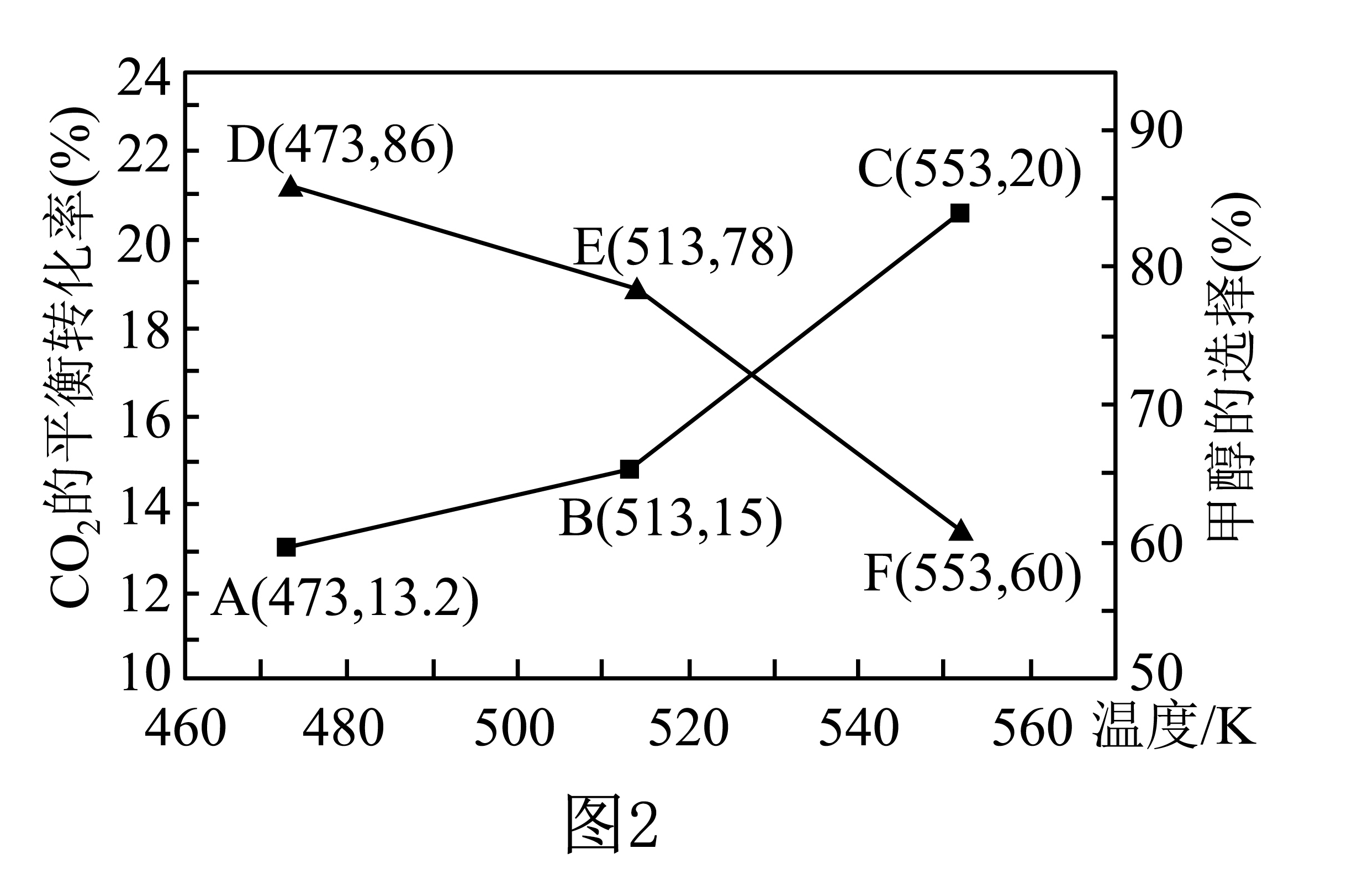
$\text{C}{{\text{H}}_{3}}\text{OH}$的选择性$ =\dfrac{ {n}\left( 生成\text{C}{{\text{H}}_{3}}\text{OH}消耗的\text{C}{{\text{O}}_{2}} \right)}{ {n}\left( 消耗\text{C}{{\text{O}}_{2}}的总量 \right)}\times 100\%$，温度对催化剂的影响可以忽略。

①根据图中数据，温度选择                $\rm K($填标号$\rm )$，达到平衡时反应体系内甲醇的产量最高。

$\rm a$．$\rm 473$    $\rm b$．$\rm 513$    $\rm c$．$\rm 553$

②在图示温度范围内，随着温度的升高，$\text{C}{{\text{O}}_{2}}$的平衡转化率                $\rm ($填“升高”“降低”或“不变”，下同$\rm )$，甲醇的选择性                ，甲醇的选择性变化的原因是                。

$\\rm c$；升高；降低；当温度升高时反应$\\rm I$和Ⅲ平衡逆向移动，而反应Ⅱ平衡正向移动

①令$n\rm (CO_{2})=1\;\rm mol$，$n\rm (H_{2})=3\;\rm mol$，温度为$\rm 473\;K$时，生成甲醇的物质的量为$\rm 1\times 13.2\%\times 86\%\;mol=0.11352\;\rm mol$；温度为$\rm 513\;K$时，生成甲醇的物质的量为$\rm 1\times 15\%\times 78\%\;mol=0.117\;\rm mol$；温度为$\rm 553\;K$时，生成甲醇的物质的量为$\rm 1\times 21\%\times 60\%\;mol=0.126\;\rm mol$；因此温度为$\rm 553\;K$时，达到平衡，反应体系内甲醇的产量最高；

②随着温度的升高，$\rm CO_{2}$的平衡转化率增加但甲醇的选择率降低，原因为当温度升高时反应Ⅰ和$\rm III$平衡逆向移动，而反应Ⅱ平衡正向移动且幅度更大，所以$\rm CO_{2}$的转化率增加，但甲醇的选择性却降低；

温度${{ {T}}_{2}}$时，在容积不变的密闭容器中，充入$0.5\text{ mol C}{{\text{O}}_{2}}\rm (g)$和$1.0\;\rm \text{mol}{{\text{ H}}_{2}}\rm (g)$，起始压强为$ {p\;\rm kPa}$，$\rm 10\;\rm min$达平衡时生成$0.3\;\rm \text{mol}{{\text{ H}}_{2}}\text{O}\rm (g)$，测得压强为$\dfrac{\text{2}}{\text{3}} p\;\rm kPa$。则反应过程中的热效应为                $\rm kJ$，若反应速率用单位时间内分压变化表示，则$\rm 10\;\rm min$内生成$\text{C}{{\text{H}}_{3}}\text{OH}$的反应速率$ {v}\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)$为                $ \text{kPa}\cdot \text{mi}{{\text{n}}^{-1}}$，反应Ⅱ的压强平衡常数${{ {K}}_{\text{p}}}\rm =$                。$\rm ($已知：分压$\rm =$总压$\rm \times $该组分物质的量分数$\rm )$

$\\rm -9.145$；$ 0.0167p($或$\\dfrac{ {p}}{60}\\rm )$；$\\rm 0.375$或$\\dfrac{3}{8}$

起始气体总物质的量为$\rm 1.5\;\rm mol$，压强$ p\;\rm kPa$，平衡状态压强$\dfrac{2}{3} p\;\rm kPa$，则平衡气体总物质的量为$\rm 1\;\rm mol$，$\rm 10\;\rm min$达平衡时生成$\rm 0.3\;\rm mol\;\rm H_{2}O(g)$，列三段式：

反应$\rm I$ $\begin{matrix} {} & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & \text{3}{{\text{H}}_{\text{2}}}\left( \text{g} \right) & \rightleftharpoons & \text{C}{{\text{H}}_{\text{3}}}\text{OH}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) \\ 起始量\text{/mol} & 0.5 & {} & \text{1}\text{.0} & {} & \text{0} & {} & \text{0} \\转化量 \text{/mol} & {x} & {} & {3x} & {} & {x} & {} & {x} \\ 平衡量\text{/mol} & {} & {} & {} & {} & {} & {} & {} \\ \end{matrix}$

反应$\rm II\begin{matrix} {} & \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\left( \text{g} \right) & \rightleftharpoons & \text{CO}\left( \text{g} \right) & + & {{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right) \\ 起始量\text{/mol} & 0.5 & {} & \text{1}\text{.0} & {} & \text{0} & {} & \text{0} \\ 转化量\text{/mol} & {y} & {} & {y} & {} & {y} & {} & {y} \\平衡量 \text{/mol} & {} & {} & {} & {} & {} & {} & {} \\ \end{matrix}$

$x+y=0.3$、$(0.5-x-y)+(1-3x-y)+(x+y)+(x+y) =1$，解得$x=0.25$，$y=0.05$，则$T_{2}$时反应过程中的热效应为$\rm 0.25\;\rm mol\times 45.4\;\rm kJ/mol-0.05\;\rm mol\times 44.1\;\rm kJ/mol=9.145\;\rm kJ$；

生成甲醇物质的量$\rm 0.25\;\rm mol$，甲醇分压${ p\rm(CH_{3}OH)}=\dfrac{\text{0} {.25\;\rm mol}}{\text{1} {.5\;\rm mol}}\times {p\rm\;kPa}=\dfrac{{p}}{6}\text{ kPa}$，则$\rm 10\;\rm min$内生成$\rm CH_{3}OH$的反应速率$ {v\rm(CH_{3}OH)}=\dfrac{\dfrac{{p}}{6}\text{ kPa}}{10\;\rm \text{min}}=\dfrac{{p}}{60}\text{ kPa}\cdot \text{mi}{{\text{n}}^{\text{-1}}}$；

反应Ⅱ中各物质的分压为：${ p\rm(CO_{2})}=\dfrac{\text{0}\text{.2}}{\text{1}\text{.5}}\times {p\rm\;kPa}$，${p\rm(H_{2})}=\dfrac{\text{0}\text{.2}}{\text{1}\text{.5}}\times {p\rm\;kPa}$，${p\rm(H_{2}O)}=\dfrac{\text{0}\text{.3}}{\text{1}\text{.5}}\times {p\rm\;kPa}$，${p\rm(CH_{3}OH)}=\dfrac{\text{0}\text{.05}}{\text{1}\text{.5}}\times {p\rm\;kPa}$，反应Ⅱ的平衡常数${{ {K}}_{\text{p}}}=\dfrac{\left( \dfrac{0.05}{1.5}{p} \right)\times \left( \dfrac{0.3}{1.5}{p} \right)}{\left( \dfrac{0.2}{1.5}{p} \right)\times \left( \dfrac{0.2}{1.5}{p} \right)}=0.375$。