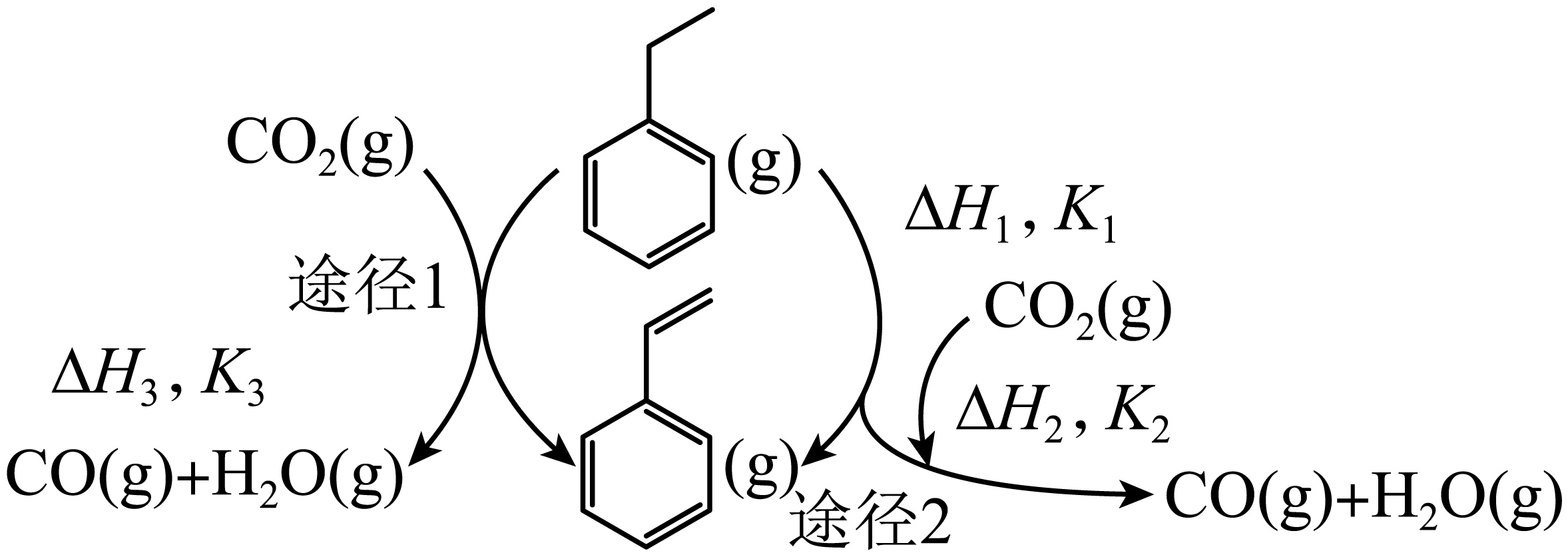
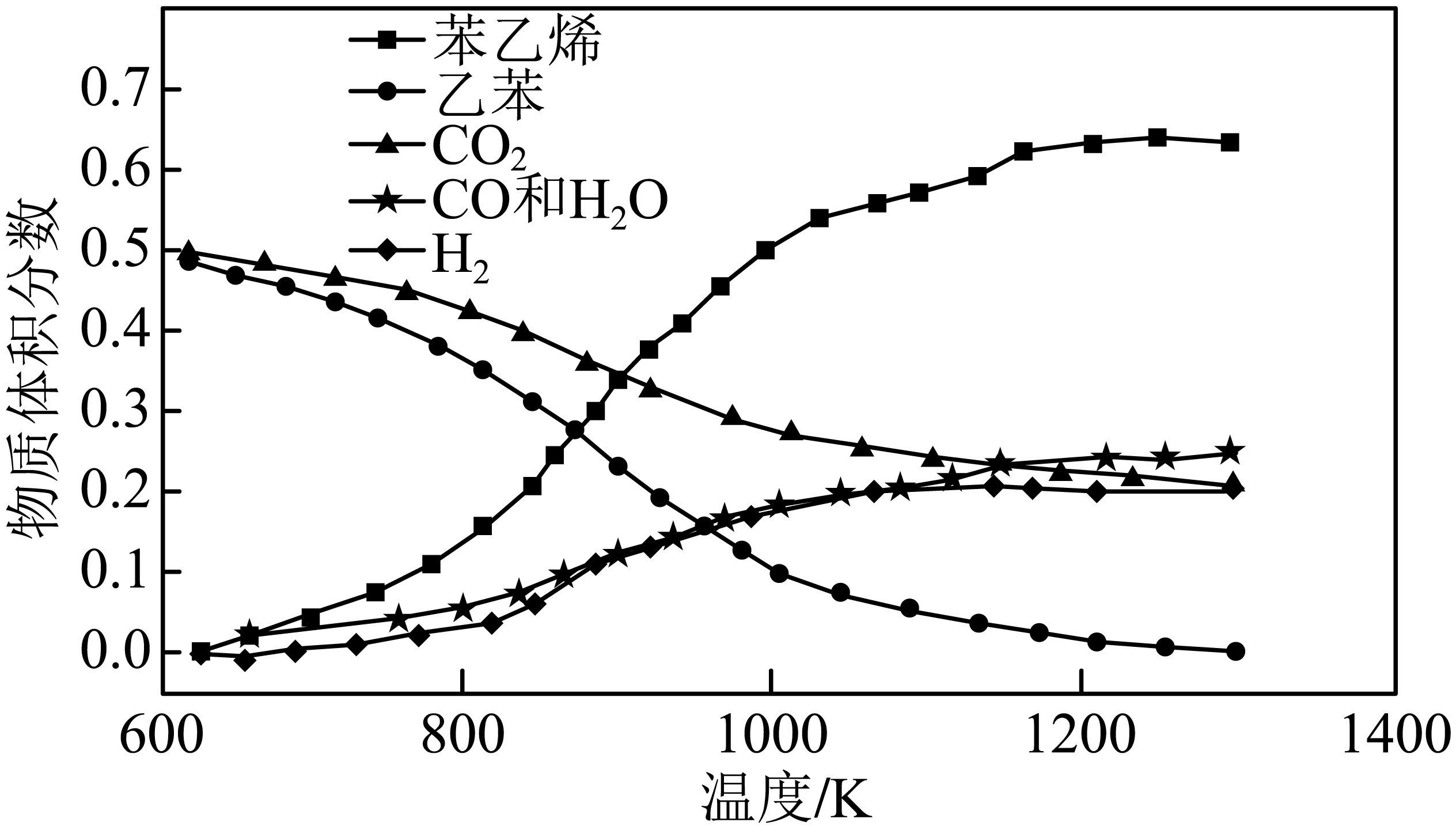
$\text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right)+$$\rm (g)\overset{催化剂}{\mathop{\rightleftharpoons }}\,$$\rm (g)\text{+CO}\left( \text{g} \right)+{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right)$平衡常数$K_{3}=$                $($用含$K_{1}$、$K_{2}$的代数式表达$)$。向刚性容器中充入等物质的量$\rm CO_{2}$和乙苯，发生途径$\rm 1$反应，不同温度下测得平衡时各物质的体积分数如下图，可推知随温度升高${{ {K}}_{\text{3}}}$                $\rm ($填“增大”或“减小”$\rm )$，相同温度下$\rm CO_{2}$转化率低于乙苯，推知发生了副反应$\text{CO}\left( \text{g} \right)+{{\text{H}}_{\text{2}}}\text{O}\left( \text{g} \right)\rightleftharpoons \text{C}{{\text{O}}_{\text{2}}}\left( \text{g} \right)+{{\text{H}}_{\text{2}}}\left( \text{g} \right)$，由图象知该反应的$ \Delta H$                $\rm 0$。

$ K_{1}K_{2}$；增大；$\\rm \\gt $

根据图$\rm 1$所示信息可知，途径$\rm 2$反应分别为：$\rm I$．$\rm (g)$ $\rightleftharpoons $${\rm (g)+H_{2}(g)}\qquad K_{1}$；

$\rm I I$．${\rm CO_{2}(g)+H_{2}(g)\rightleftharpoons \rm CO(g)+H_{2}O(g)}\qquad K_{2}$，

途径$\rm 1$反应为：$\rm II I$．$\rm CO_{2}(g)+$$\rm (g) \overset{催化剂 }{\underset{ }{\rightleftharpoons}}$${\rm (g)+CO(g)+H_{2}O(g)}\qquad K_{3}$，则有$\rm III=I+II$，故$ K_{3}= K_{1}K_{2}$；

由图$\rm 2$所示信息可知，温度越高苯乙烯的体积分数越大，说明反应的化学平衡正向移动，故正反应为吸热反应$\Delta H_{3}\gt 0$；则升温平衡常数$ K_{3}$增大；相同温度下$\rm CO_{2}$转化率低于乙苯，说明副反应生成的$\rm CO_{2}$随温度升高也越来越多，即升高温度副反应$\rm CO(g)+H_{2}O(g)\rightleftharpoons \rm CO_{2}(g)+H_{2}(g)$化学平衡正向移动，由图象知该反应$\Delta H\gt 0$；

某团队研究途径$\rm 2$，找到无需$\rm CO_{2}$的乙苯直接脱氢的高效催化剂，原理如图：$\left( \text{g} \right)\overset{催化剂}{\mathop{\rightleftharpoons }} {{\text{H}}_{\text{2}}}\left( \text{g} \right)+$$\left( \text{g} \right)\qquad\Delta { H}$。工业上，通常在乙苯$\rm (EB)$蒸气中掺混$\rm N_{2}($原料气中乙苯和$\rm N_{2}$的物质的量之比为$\rm 1: 10$；$\rm N_{2}$不参与反应$\rm )$，控制反应温度$\rm 600\;\rm ^\circ\rm C$，并保持体系总压为$\rm 0.1\;MPa$不变的条件下进行反应。在不同反应温度下，乙苯的平衡转化率和某催化剂作用下苯乙烯的选择性$\rm ($指除了$\rm H_{2}$以外的产物中苯乙烯的物质的量分数$\rm )$示意图如下。

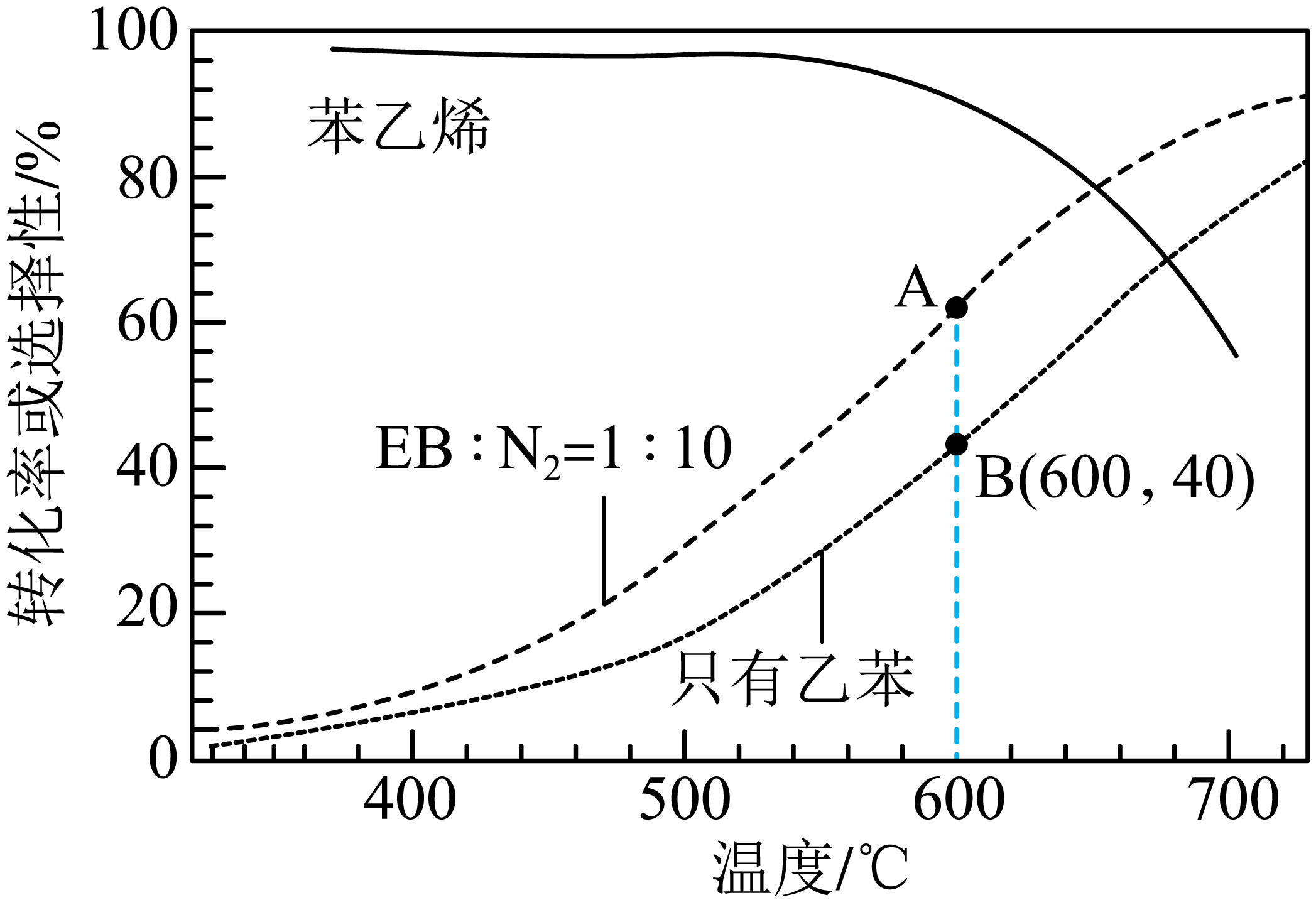
①掺入$\rm N_{2}$能提高乙苯的平衡转化率，解释说明该事实                。

②$\rm AB$两点对应的正反应速率较小的是                。

③用平衡分压代替平衡浓度计算$\rm 600\;\rm ^\circ\rm C$时的平衡常数$ K\rm_{p}=$                $\rm MPa$。

④控制反应温度为$\rm 600\;\rm ^\circ\rm C$的理由是                。

正反应方向气体分子数增加，加入氮气稀释，相当于起减压的效果，平衡正向移动，乙苯的转化率提高；$\\rm A$；$\\rm 0.019$；$\\rm 600\\;\\rm ^\\circ\\rm C$时，乙苯的转化率和苯乙烯的选择性均较高，温度过低，反应速率慢，转化率低；温度过高，选择性下降，高温还可能使催化剂失活，且能耗大

①该反应正反应气体分子数增加，恒压条件下加入氮气，相当于减压，减小压强，化学平衡正向移动，乙苯的转化率增大；

②由题图可知，$\rm A$、$\rm B$两点对应的温度和压强都相同，$\rm A$点是乙苯和氮气的混合气体，$\rm B$点是纯乙苯，则$\rm B$点乙苯浓度大于$\rm A$ 点，浓度越大反应速率越大，则正反应速率$\rm B$点大于$\rm A$点，故正反应速率较小的是$\rm A$；

③由题图可知，反应温度为$\rm 600\;\rm ^\circ\rm C$，并保持体系总压为$\rm 0.1\;MPa$时，乙苯转化率为$\rm 40\%$，设乙苯起始物质的量为$\rm 1\;\rm mol$，则依据题意可建立如下三段式：$\begin{matrix} {} &乙苯 \left( \text{g} \right) & \rightleftharpoons & {{\text{H}}_{\text{2}}}\left( \text{g} \right) \\起始量 \text{(mol)} & 1 & {} & \text{0} \\ 转化量\text{(mol)} & \text{0}\text{.4} & {} & 0.4 \\平衡量 \text{(mol)} & 0.6 & {} & 0.4 \\ \end{matrix}\begin{matrix} +苯乙烯\text{(g)} \\ \text{0} \\ 0.4 \\ 0.4 \\ \end{matrix}$，平衡时总物质的量为$\rm 1.4\;\rm mol$，乙苯的平衡分压为$\dfrac{0.6}{1.4}\times \rm 0.1\;MPa$，苯乙烯和氢气的平衡分压均为$\dfrac{0.4}{1.4}\times \rm 0.1\;MPa$，则$\rm 600\;\rm ^\circ\rm C$时的平衡常数${{K}_{\text{p}}}=\dfrac{{{(\dfrac{0.4}{1.4}\times 0.1\text{ MPa})}^{2}}}{\dfrac{0.6}{1.4}\times 0.1\text{ MPa}}\approx 0.019\;\rm MPa$；

④根据题图可知，$\rm 600\; ^\circ\rm C$时，乙苯的转化率和苯乙烯的选择性均较高，该反应为吸热反应，若温度过低，化学反应速率慢，乙苯的转化率低；若温度过高，苯乙烯的选择性下降，高温还可能使催化剂失活，且能耗大；

实验测得，乙苯脱氢的速率方程为${{ {v}}_正{}}={{{k}}_正{}}{{{p}}_ {乙苯}}$，${{ {v}}_逆{}}={{{k}}_逆{}}{{ {p}}_ {苯乙烯}}{{ {p}}_ {氢气}} ({{{k}}_正{}}$、${{{k}}_逆{}}$为速率常数，只与温度有关$\rm )$，下图中④代表$\lg{{{k}}_正{}}$随$ 1/T$的变化关系，则能代表$\lg{{{k}}_逆{}}$随$ 1/T$的变化关系的是                $\rm ($填序号$\rm )$。

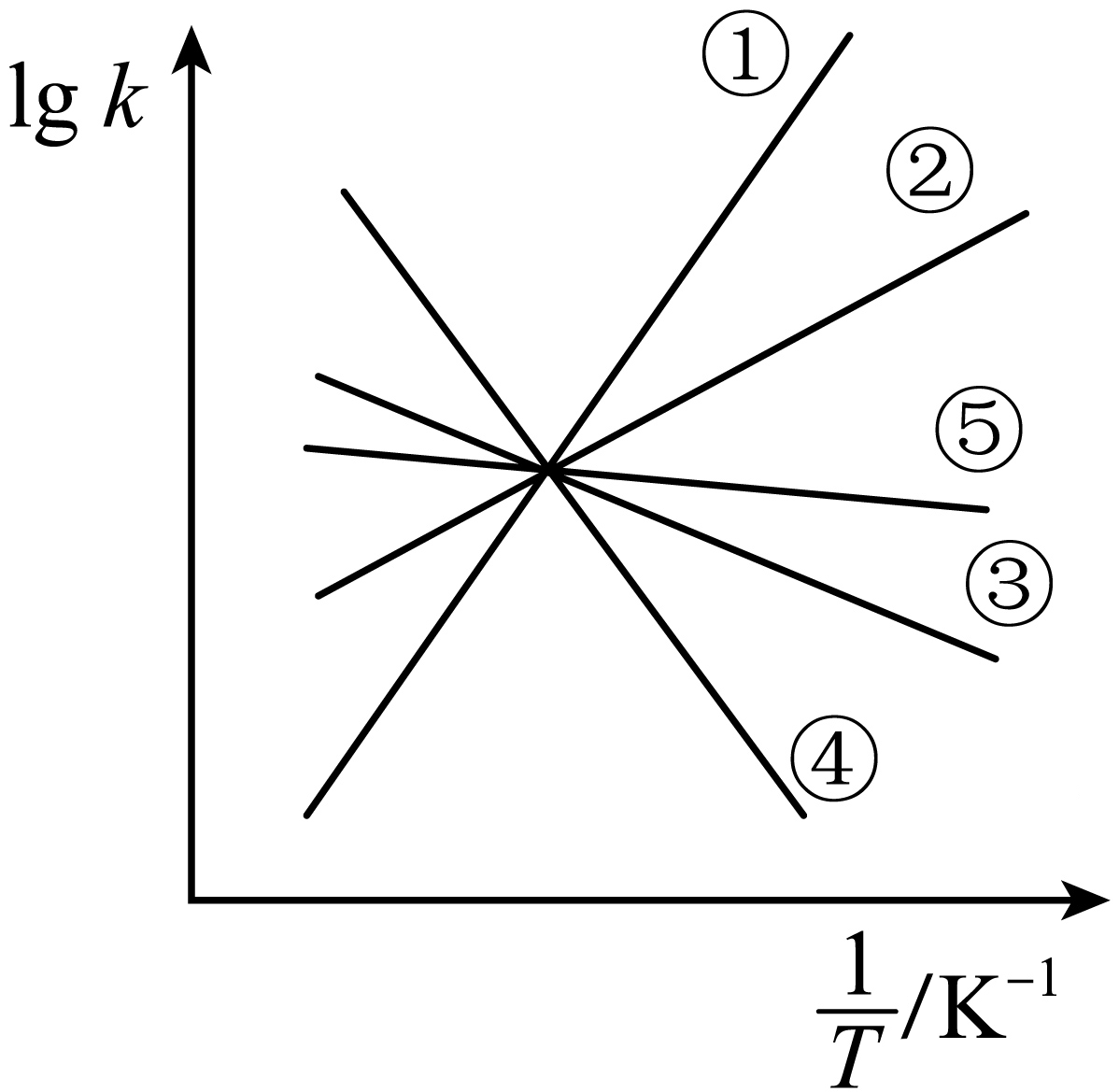
③或⑤

实验测得，乙苯脱氢的速率方程为${{ {v}}_正{}}={{{k}}_正{}}{{{p}}_ {乙苯}}$，${{ {v}}_逆{}}={{{k}}_逆{}}{{ {p}}_ {苯乙烯}}{{ {p}}_ {氢气}} ({{{k}}_正{}}$、${{{k}}_逆{}}$为速率常数，只与温度有关$\rm )$，达到平衡时，${v} _{正}={v}\rm _{逆}$，即$ k_{正}p_{乙苯}=k_{逆}p_{苯乙烯}p_{氢气}$，则有$\dfrac{{{{k}}_正{}}}{{{{k}}_逆{}}}=\dfrac{{{{p}}_ {苯乙烯}}{{{p}}_ {氢气}}}{{{{p}}_ {乙苯}}} =K $，由上一问可知乙苯脱氢反应正反应是一个吸热反应，故温度越高平衡正向移动，正反应速率加快的倍数大于逆反应速率增大的倍数，即$\dfrac{{{{k}}_正{}}}{{{{k}}_逆{}}}$随温度升高而增大，且${{{k}}_正{}}$增大的倍数大于${{{k}}_逆{}}$增大的倍数，图像从右向左是升温，若④代表$\lg{{{k}}_正{}}$随$\dfrac{1}{{T}}$的变化关系，则③或⑤代表$\lg k_{逆}$随$\dfrac{1}{{T}}$的变化关系。