已知${{\text{H}}_{2}}、\text{N}{{\text{H}}_{3}}$的燃烧热（$\Delta H$）分别为$\textit{a}\;\rm kJ\cdot \text{mo}{{\text{l}}^{-1}}$，$\textit{b}\rm\ kJ\cdot \text{mo}{{\text{l}}^{-1}}$，写出合成氨的热化学反应方程式                。

${{\\text{N}}_{2}}\\left( \\text{g} \\right)+3{{\\text{H}}_{2}}\\left( \\text{g} \\right)\\rightleftharpoons 2\\text{N}{{\\text{H}}_{3}}\\left( \\text{g} \\right)\\text{ }\\qquad\\Delta\\!\\!\\textit{ H}=\\left( 3\\textit{a}-2\\textit{b} \\right)\\;\\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$

燃烧热是在$\rm 101$ $\rm kPa$时，$\rm 1$ $\rm mol$纯物质完全燃烧生成指定产物时所放出的热量；已知${{\text{H}}_{2}}、\text{N}{{\text{H}}_{3}}$的燃烧热（$\Delta \textit{H}$）分别为$a\;\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，$b\;\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，则：

①${{\text{H}}_{\text{2}}}\left( \text{g} \right)+\dfrac{\text{1}}{\text{2}}{{\text{O}}_{\text{2}}}\left( \text{g} \right)\underset{{}}{\overset{{}}{\mathop{\rightleftharpoons }}}\,{{\text{H}}_{\text{2}}}\text{O}\left( \text{l} \right)\qquad\Delta \textit{H}=a\;\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

②$\text{N}{{\text{H}}_{3}}\left( \text{g} \right)+\dfrac{3}{\text{4}}{{\text{O}}_{\text{2}}}\left( \text{g} \right)\underset{{}}{\overset{{}}{\mathop{\rightleftharpoons }}}\,\dfrac{\text{1}}{\text{2}}{{\text{N}}_{2}}\left( \text{g} \right)+\dfrac{3}{\text{2}}{{\text{H}}_{\text{2}}}\text{O}\left( \text{l} \right)\qquad\Delta \textit{H}=b\;\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

由盖斯定律，$\rm 3\times $①$\rm -2\times $②得${{\text{N}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons 2\text{N}{{\text{H}}_{3}}\left( \text{g} \right)\qquad\Delta\!\!\textit{ H}=\left( 3\textit{a}-2\textit{b} \right)\;\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

在$\rm 500\;K$，体积为$\rm 1\;\rm L$的恒容容器中，对于合成氨反应，初始投料${{\text{N}}_{2}}\left( \text{g} \right)$为$\rm 0.2\;\rm mol$，${{\text{H}}_{2}}\left( \text{g} \right)$为$0.05\;\rm \text{mol}$，$\text{N}{{\text{H}}_{3}}\left( \text{g} \right)$为$\rm 0.15\;\rm mol$，以下可说明反应达到平衡的有                （填序号）。

①${{\text{H}}_{2}}$的体积分数不变  ②${{\text{N}}_{2}}$的物质的量分数不变  ③气体总压不变

④$\text{N}{{\text{H}}_{3}}$的分压不变  ⑤体系密度不变

①③④

①${{\text{H}}_{2}}$的体积分数不变，则平衡不再移动，说明达到平衡；  

②由题意：

$\begin{matrix} {} \\ 起始\left( \text{mol} \right) \\ 转化\left( \text{mol} \right) \\ 平衡\left( \text{mol} \right) \\ \end{matrix}\begin{matrix} {{\text{N}}_{\text{2}}}\text{(g)} \\ \text{0}\text{.2} \\ \textit{a} \\ \text{0.2}-\textit{a} \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{3}{{\text{H}}_{\text{2}}}\text{(g)} \\ \text{0}\text{.05} \\ 3\textit{a} \\ \text{0.05}-3\textit{a} \\ \end{matrix}\begin{matrix} \underset{{}}{\overset{{}}{\mathop{\rightleftharpoons }}}\, \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{2N}{{\text{H}}_{\text{3}}}\text{(g)} \\ \text{0}\text{.15} \\ 2\textit{a} \\ \text{0.15}-2\textit{a} \\ \end{matrix}$

反应后总的物质的为$ 0.4-2a$，则${{\text{N}}_{2}}$的物质的量分数$\dfrac{\text{0}.2-a}{\text{0}.4-2a}=0.5$，为定值，其不变，不能说明反应平衡；  

③恒容容器中进行气体分子数减小的反应，气体总压不变，则平衡不再移动，说明达到平衡；

④$\text{N}{{\text{H}}_{3}}$的分压不变，则平衡不再移动，说明达到平衡；  

⑤容器体积和气体总质量始终不变，则混合气体的密度始终不变，因此不能说明反应已达平衡；

故选：①③④

在不同压强下，以两种不同组成进料，反应达平衡时氨的摩尔分数与温度的计算结果如图所示（物质$\rm i$的摩尔分数：${{\textit{x}}_{\text{i}}}=\dfrac{{{\textit{n}}_{\text{i}}}}{{{\textit{n}}_{总}}}$）。其中一种进料组成为$x_{\mathrm{H}_2}=0.75$，$x_{\mathrm{N}_2}=0.25$，另一种为$x_{\mathrm{H}_2}=0.675$、$x_{\mathrm{N}_2}=0.225$、${{\textit{x}}_{\text{Ar}}}=0.10$。

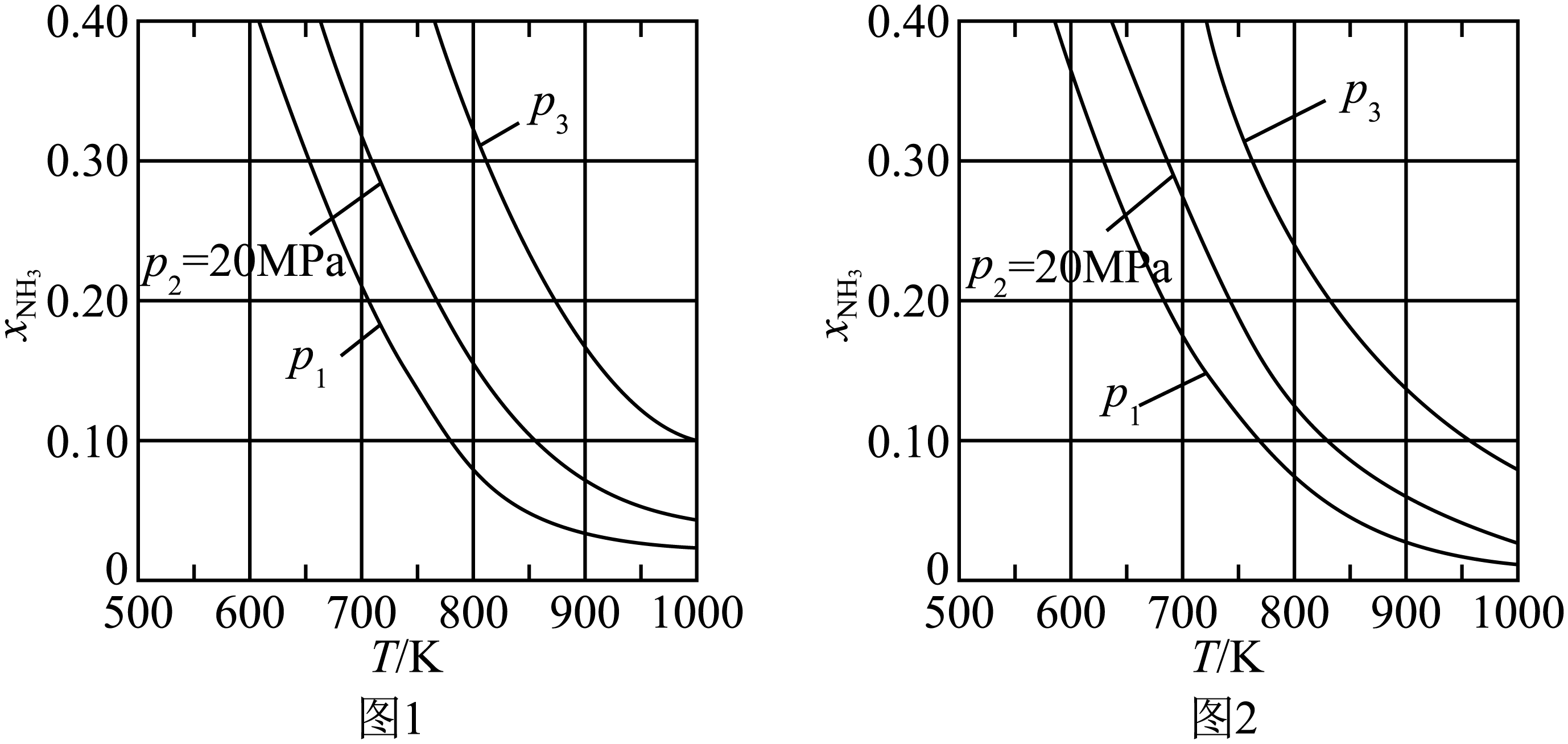
①图中压强由小到大的顺序为                ，判断的依据是                。

②进料组成中含有惰性气体$\rm Ar$的图是                。

③图$\rm 1$中，当$p_2=20\ \mathrm{MPa}$、${{\textit{x}}_{\text{N}{{\text{H}}_{3}}}}=0.20$时，氮气转化率$\alpha=$                （保留$\rm 3$位有效数字），该温度时，反应$\dfrac{1}{2}{{\text{N}}_{2}}\left( \text{g} \right)+\dfrac{3}{2}{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{N}{{\text{H}}_{3}}\left( \text{g} \right)$的平衡常数${{\textit{K}}_{\text{p}}}=$                ${{(\text{MPa})}^{-1}}$（化为最简式）。

${{\\textit{p}}_{1}}\\lt {{\\textit{p}}_{2}}\\lt {{\\textit{p}}_{3}}$ ；合成氨的反应为气体分子数减少的反应，压强越大平衡时氨的摩尔分数越大 ；图$\\rm 2$；$\\rm 33.3\\%$； $\\sqrt{\\dfrac{1}{432}}$（或$\\dfrac{\\sqrt{3}}{36}$）

①合成氨的反应为气体分子数减小的反应，压强越大越有利于氨的合成，因此压强越大平衡时氨的摩尔分数越大，结合图中信息可知，在相同温度下，反应达平衡时氨的摩尔分数${{\textit{p}}_{1}}\lt {{\textit{p}}_{2}}\lt {{\textit{p}}_{3}}$，因此，图中压强由小到大的顺序为${{\textit{p}}_{1}}\lt {{\textit{p}}_{2}}\lt {{\textit{p}}_{3}}$；判断的依据是：合成氨的反应为气体分子数减少的反应，压强越大平衡时氨的摩尔分数越大。

②对比图$\rm 1$和图$\rm 2$中的信息可知，在相同温度和相同压强下，图$\rm 2$中平衡时氨的摩尔分数较小。在恒压下充入惰性气体，反应混合物中各组分的浓度减小，各组分的分压也减小，化学平衡要朝气体分子数增大的方向移动，因此，充入惰性气体不利于合成氨，进料组成中含有惰性气体的图是图$\rm 2$。

③图$\rm 1$中，进料组成为两者物质的量之比为$\rm 3:1$，假设进料中氢气和氮气的物质的量分别为$\rm 3\;\rm mol$和$\rm 1\;\rm mol$，达到平衡时氮气的变化量为$a\rm\ mol$，则有：

$\begin{matrix} {} \\ 起始\left( \text{mol} \right) \\ 转化\left( \text{mol} \right) \\ 平衡\left( \text{mol} \right) \\ \end{matrix}\begin{matrix} {{\text{N}}_{\text{2}}}\text{(g)} \\ \text{1} \\ \textit{a} \\ 1-a \\ \end{matrix}\begin{matrix} + \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{3}{{\text{H}}_{\text{2}}}\text{(g)} \\ \text{3} \\ 3a \\ 3-3a \\ \end{matrix}\begin{matrix} \underset{{}}{\overset{{}}{\mathop{\rightleftharpoons }}}\, \\ {} \\ {} \\ {} \\ \end{matrix}\begin{matrix} \text{2N}{{\text{H}}_{\text{3}}}\text{(g)} \\ \text{0} \\ 2a \\ 2a \\ \end{matrix}$

总的物质的量为$ 4-2a$，当$p_2=20\ \mathrm{MPa}$、${{\textit{x}}_{\text{N}{{\text{H}}_{3}}}}=0.20$时，则$\dfrac{2\textit{a}}{4-2\textit{a}}=0.20$，$\textit{a}=\dfrac{1}{3}$，氮气转化率$\alpha=\dfrac{3\times \dfrac{1}{3}}{3}\times \text{100 }\!\!\%=33.3\%$；平衡时氮气、氢气、氨气的物质的量分别为$\dfrac{2}{3}\rm\ mol$、$\rm 2\;\rm mol$、$\dfrac{2}{3}\rm\ mol$，其物质的量分数分别为$\dfrac{1}{5}$、$\dfrac{3}{5}$、$\dfrac{1}{5}$，则该温度下反应${{\text{N}}_{2}}\left( \text{g} \right)+3{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons 2\text{N}{{\text{H}}_{3}}\left( \text{g} \right)$的平衡常数${{\textit{K}}_{\text{p}}}=\dfrac{{{\left( \dfrac{1}{5}\times 20 \right)}^{2}}}{\left( \dfrac{1}{5}\times 20 \right)\times {{\left( \dfrac{3}{5}\times 20 \right)}^{\text{3}}}}\;{{(\text{MPa})}^{-2}}=\dfrac{16}{4\times {{12}^{\text{3}}}}\;{{(\text{MPa})}^{-2}}$，故反应$\dfrac{1}{2}{{\text{N}}_{2}}\left( \text{g} \right)+\dfrac{3}{2}{{\text{H}}_{2}}\left( \text{g} \right)\rightleftharpoons \text{N}{{\text{H}}_{3}}\left( \text{g} \right)$的平衡常数${{\textit{K}}_{\text{p}}}=\sqrt{\dfrac{16}{4\times {{12}^{\text{3}}}}\;{{(\text{MPa})}^{-2}}}=\sqrt{\dfrac{1}{432}}\;{{(\text{MPa})}^{-1}}$（或$\dfrac{\sqrt{3}}{36}\;{{(\text{MPa})}^{-1}}$）。