则$\rm \Delta \textit{H}_{1}=$                $\rm \;\rm kJ/mol$。

$\\rm -134$

根据盖斯定律，反应Ⅱ$\rm \times 2-$反应Ⅲ$\rm =$反应Ⅰ，则$\rm \text{ }\!\!\Delta{{\textit{H}}_{\text{1}}}\text{=2 }\!\!\Delta{{\textit{H}}_{\text{2}}}-\text{ }\!\!\Delta{{\textit{H}}_{\text{3}}}=2\times \left( \text{+98\;\rm kJ/mol} \right)-\left( \text{+330\;\rm kJ/mol} \right)=-134\;\text{kJ/mol}$；

向温度为$ T\;^\circ\rm C$的刚性容器中，充入$\rm 1\;\rm mol\;\rm SiCl_{4}(g)$和$\rm 2\;\rm mol\;\rm Zn(g)$，起始压强为$p_{0}$ $\rm kPa$条件下发生上述反应，达到平衡后，测得反应体系中$\rm Zn$、$\rm ZnCl_{2}$物质的量分数分别为$\rm 35\%$、$\rm 40\%$，则$\rm Si$的物质的量为                $\rm \;\rm mol$，反应Ⅰ的分压表示的平衡常数$K_\rm {p}=$                $\rm \text{kP}{{\text{a}}^{\text{-1}}}\rm ($用含$p_{0}$代数式表示$\rm )$，若再向刚性容器中充入一定量的$\rm Zn(g)$，重新达平衡后，则分压$ p\rm(SiCl_{2})$将                $\rm ($填“增大”、“减小”或“不变”$\rm )$。

$\\rm \\dfrac{1}{3}$ ；$\\rm \\dfrac{720}{49{{\\textit{p}}_{0}}}$； 减小

刚性容器中发生$\rm SiCl_{4}(g)+2Zn(g)⇌Si(s)+2ZnCl_{2}(g)$及$\rm SiCl_{4}(g)+Zn(g)⇌SiCl_{2}(g)+ZnCl_{2}(g)$，利用三段式分析

$\rm \begin{matrix} {} & \text{SiC}{{\text{l}}_{\text{4}}}\left( \text{g} \right) & \text{+2Zn}\left( \text{g} \right) & \rightleftharpoons & \text{Si}\left( \text{s} \right) & \text{+2ZnC}{{\text{l}}_{\text{2}}}\left( \text{g} \right) \\ 初始\text{/mol} & \text{1} & \text{2} & {} & \text{0} & \text{0} \\ 转化\text{/mol} & \textit{x} & 2\textit{x} & {} & \textit{x} & 2\textit{x} \\ 平衡\text{/mol} & {} & {} & {} & \textit{x} & {} \\ \end{matrix}\begin{matrix} \Delta\!\!\textit{ n}\left(气体 \right) \\ {} \\ \textit{x} \\ {} \\ \end{matrix}$，$\rm \begin{matrix} {} & \text{SiC}{{\text{l}}_{\text{4}}}\left( \text{g} \right) & \text{+Zn}\left( \text{g} \right) & \rightleftharpoons & \text{SiC}{{\text{l}}_{\text{2}}}\left( \text{g} \right) & \text{+ZnC}{{\text{l}}_{\text{2}}}\left( \text{g} \right) \\ 初始\text{/mol} & 1-\textit{x} & 2-2\textit{x} & {} & \text{0} & 2\textit{x} \\ 转化\text{/mol} & \textit{y} & \textit{y} & {} & \textit{y} & \textit{y} \\ 平衡\text{/mol} & 1-\textit{x}-\textit{y} &2-2\textit{x}-\textit{y} & {} & \textit{y} & 2\textit{x}+\textit{y} \\ \end{matrix}\begin{matrix} \Delta\!\!\textit{ n}\left(气体 \right) \\ {} \\ 0 \\ {} \\ \end{matrix}$

平衡时气体总物质的量为$\rm \textit{n}\left( 总\right)=\left( 3-\textit{x}\right)\;\text{mol}$，列式得$\rm \begin{cases} \dfrac{2-2\textit{x}-\textit{y}}{3-\textit{x}}=35\% \\ \dfrac{2\textit{x}+\textit{y}}{3-\textit{x}}=40\% \\ \end{cases}$，解得$\rm \begin{cases} \textit{x}=\dfrac{1}{3} \\ \textit{y}=\dfrac{2}{5} \\ \end{cases}$，则平衡时，$\rm Si$的物质的量为$\rm \dfrac{1}{3}\;\text{mol}$，$\rm \textit{n}\left( \text{SiC}{{\text{l}}_{\text{4}}} \right)=\left( 1-\dfrac{1}{3}-\dfrac{2}{5} \right)\;\text{mol}=\dfrac{4}{15}$；平衡时$\rm \textit{n}\left(总 \right)=\left( 3-\textit{x} \right)\text{mol=}\left(3-\dfrac{1}{3} \right)\;\text{mol}=\dfrac{8}{3}\;\text{mol}$，则根据$\rm \dfrac{\textit{n}\left(初 \right)}{\textit{n}\left( 平\right)}=\dfrac{\textit{p}\left( 初\right)}{\textit{p}\left(平 \right)}$，即$\rm \dfrac{3\;\rm \text{mol}}{\dfrac{8}{3}\;\text{mol}}=\dfrac{{{\textit{p}}_{0}}}{\textit{p}\left(总 \right)}$，$\rm \textit{p}\left( 总\right)=\dfrac{8}{9}{{\textit{p}}_{0}}$，反应Ⅰ的分压表示的平衡常数$\rm {{\textit{K}}_{\text{p}}}=\dfrac{{{\textit{p}}^{\text{2}}}\left( \text{ZnC}{{\text{l}}_{\text{2}}} \right)}{\textit{p}\left( \text{SiC}{{\text{l}}_{\text{4}}} \right)\cdot {{\textit{p}}^{\text{2}}}\left( \text{Zn} \right)}=\dfrac{{{\left( \dfrac{8}{9}{{\textit{p}}_{0}}\times 40\% \right)}^{2}}}{\left( \dfrac{8}{9}{{\textit{p}}_{0}}\times \dfrac{\dfrac{4}{15}}{\dfrac{8}{3}} \right)\cdot {{\left( \dfrac{8}{9}{{\textit{p}}_{0}}\times 35\% \right)}^{2}}}=\dfrac{720}{49{{\textit{p}}_{0}}}\;\text{kP}{{\text{a}}^{\text{-1}}}$；若再向刚性容器中充入一定量的$\rm Zn(g)$，反应Ⅰ及反应Ⅱ平衡正移，重新达平衡后，$\rm \textit{n}\left( \text{SiC}{{\text{l}}_{4}} \right)$减小，$\rm \textit{n}\left( \text{SiC}{{\text{l}}_{2}} \right)$增大，由于温度不变，反应Ⅲ的平衡常数不变，而硅是固体，因此分压$\rm \textit{p}\left( \text{SiC}{{\text{l}}_{\text{2}}} \right)$将减小；

当$n\rm (Zn):\textit{n}\rm (SiCl_{4})=2:1$时，$\rm 10.0\;MPa$条件下平衡时$S\rm (Si)$随温度的变化，以及$\rm 1500\;K$条件下平衡时$S\rm (Si)$随压强的变化如图所示。

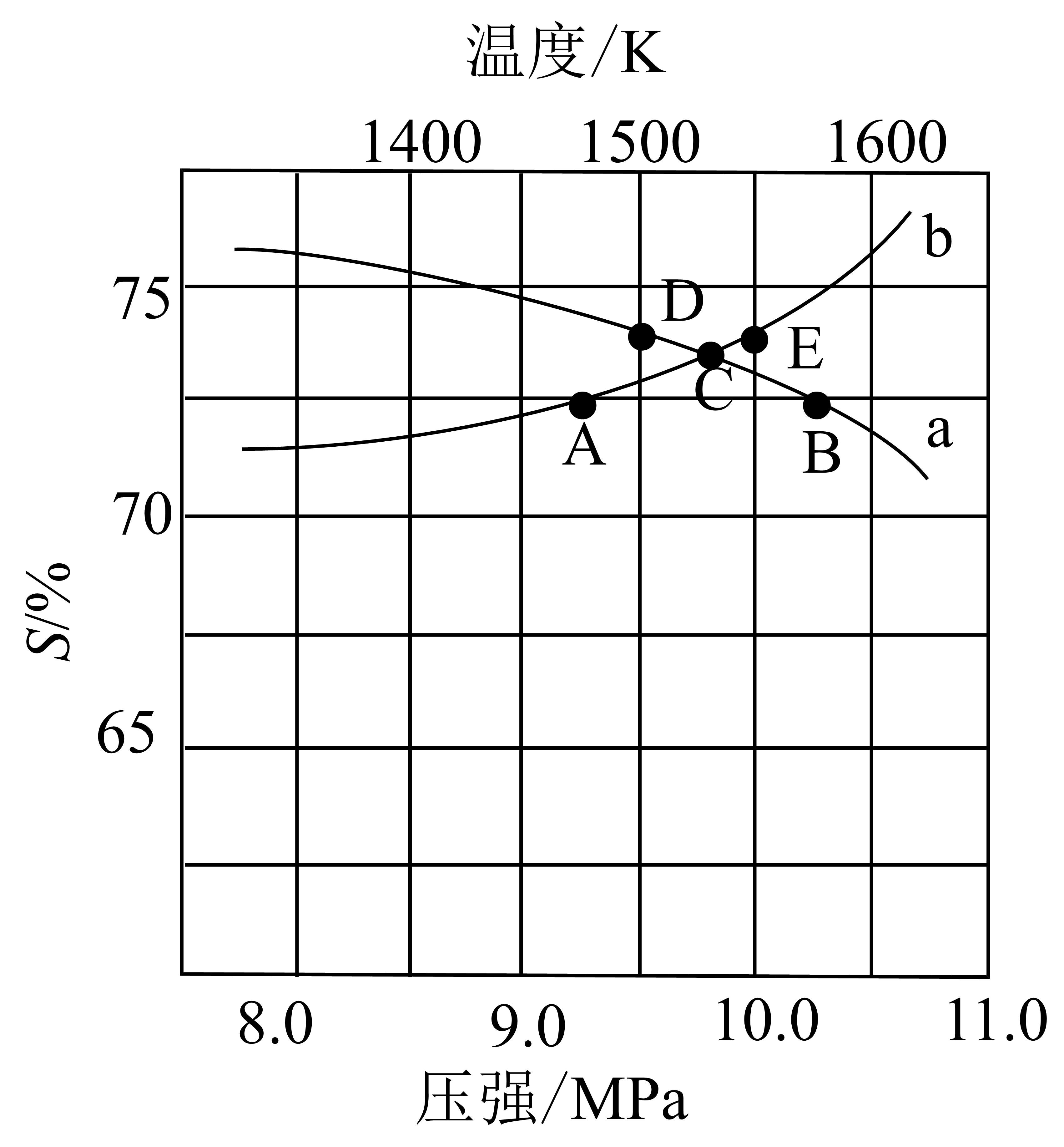
①$\rm 10.0\;MPa$条件下平衡时$S\rm (Si)$随温度的变化的曲线是                $\rm ($填“$\rm a$”或“$\rm b$”$\rm )$。

②$\rm A$、$\rm B$、$\rm C$、$\rm D$、$\rm E$五个点中，处于完全相同化学平衡状态的两个点是                。

③曲线$\rm b$呈如图所示变化趋势的原因是                。

$\\rm a$； $\\rm DE$ ；曲线$\\rm b$是 $\\rm 1500\\;K$条件下平衡时$S\\rm (Si)$随压强的变化，压强增大，反应Ⅰ平衡正向移动，反应Ⅲ平衡逆向移动，都会使$S\\rm (Si)$增大

①反应Ⅰ为放热反应，反应Ⅱ为吸热反应，温度升高，反应Ⅰ平衡逆移，反应Ⅱ平衡正移，$\rm Si$选择性降低，$\rm SiCl_{2}$选择性升高，即$S\rm (Si)$随温度升高降低，曲线$\rm a$是$S\rm (Si)$随温度的变化的曲线；

②曲线$\rm a$是$\rm 10.0\;MPa$条件下平衡时$S\rm (Si)$随温度的变化，则曲线上的点$\rm B$、$\rm C$、$\rm D$分别表示压强为$\rm 10.0\;MPa$时温度约为$\rm 1570\;K、1530\;K、1500\;K$的平衡，曲线$\rm b$是 $\rm 1500\;K$条件下平衡时$S\rm (Si)$随压强的变化，则曲线上的点$\rm A$、$\rm C$、$\rm E$分别表示温度为$\rm 1500\;K$时压强约为$\rm 9.2\;MPa、9.8\;MPa、10.0\;MPa$的平衡，故$\rm D$、$\rm E$都代表$\rm \text{1500\;K}$、$\rm \text{10.0\;MPa}$条件下的平衡，二者处于完全相同化学平衡状态；

③曲线$\rm b$是 $\rm 1500\;K$条件下平衡时$S\rm (Si)$随压强的变化，压强增大，平衡向气体体积减小的方向移动，则反应Ⅰ $\rm SiCl_{4}(g)+2Zn(g)⇌Si(s)+2ZnCl_{2}(g)$平衡正向移动，反应Ⅲ $\rm SiCl_{4}(g)+Si(s)⇌2SiCl_{2}(g)$平衡逆向移动，使$\rm Si$的物质的量增大，$\rm SiCl_{2}$物质的量减少，$\rm Si$的选择性增大