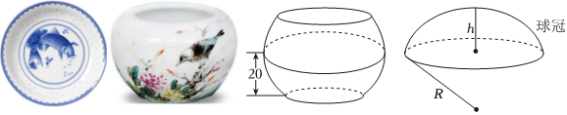
随着古代瓷器工艺的高速发展，在著名的宋代五大名窑之后，又增加了三种瓷器，与五大名窑并称为中国八大名瓷，其中最受欢迎的是景德镇窑．如图，景德镇产的青花玲珑瓷（无盖有底）的形状可视为一个球被两个平行平面所截后剩下的部分，其中球面被平面所截的部分均可视为球冠（截得的圆面是底，垂直于圆面的直径被截得的部分是高，其面积公式为$S=2\pi Rh$，其中$R$为球的半径，$h$为球冠的高）．已知瓷器的高为$38\;\rm cm$，在高为$20\;\rm cm$处有最大直径（外径）为$48\;\rm cm$，则该瓷器的表面积约为（$\pi $取$3.14$）$(\qquad)$．

$6270\\;\\rm c{{m}^{2}}$

$6275\\;\\rm c{{m}^{2}}$

$6280\\;\\rm c{{m}^{2}}$

$6300\\;\\rm c{{m}^{2}}$

根据题意可知球的半径$R=24$，上球冠的高为$24-18=6$，下球冠的高为$24-20=4$，

下底面圆的半径为$\sqrt{{{24}^{2}}-{{20}^{2}}}=4\sqrt{11}$，

$\therefore $ 该瓷器的表面积约为$4\pi\times24^{2}-2\pi\times24\times5-2\pi\times24\times4+\pi\times(4\sqrt{11})^{2}\approx6280(\rm cm^{2})$．

故选：$\rm C$