已知棱长相等的正三棱锥$P-ABC$底面的三个顶点$A,B,C$均在以$O$为球心的球面上（其中$O$为$\triangle ABC$的中心），球面与棱$PA,PB,PC$分别交于点${{A}_{1}},{{B}_{1}},{{C}_{1}}$．若球$O$的表面积为$12\pi$，则多面体${{A}_{1}}{{B}_{1}}{{C}_{1}}-ABC$的体积为                 ．

设球$O$的半径为$R$，由$4\pi{{R}^{2}}=12\pi$，得$R=\sqrt{3}$，

依题意，三棱锥$P-ABC$为正四面体，且$AO=R$，

设正四面体的棱长为$a$．在等边三角形$ABC$中，

由正弦定理可得$\dfrac{a}{\sin \dfrac{\pi}{3}}=2R$，即$\dfrac{a}{\dfrac{\sqrt{3}}{2}}=2\sqrt{3}$，解得$a=3$，

$\because PO\perp $平面$ABC$，$AO\subset $平面$ABC$，

$\therefore PO\perp AO$，

$\therefore PO=\sqrt{P{{A}^{2}}-A{{O}^{2}}}=\sqrt{{{a}^{2}}-{{R}^{2}}}=\sqrt{{{3}^{2}}-{{(\sqrt{3})}^{2}}}=\sqrt{6}$，

作$O H \perp P A$，垂足为$H$，在$\text{Rt}\triangle PAO$中，由$OH\cdot PA=PO\cdot AO$，

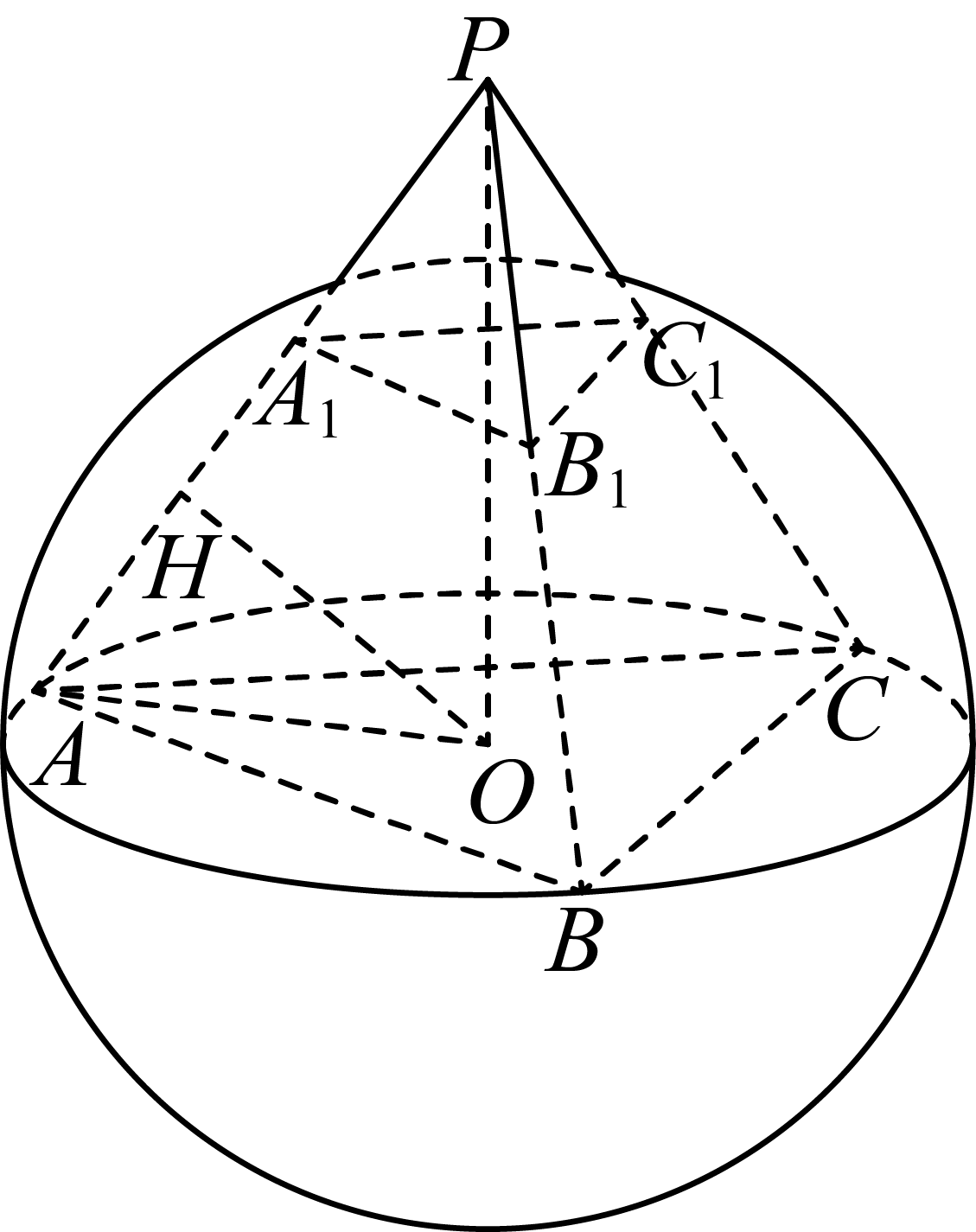
得$OH=\dfrac{PO\cdot AO}{PA}=\dfrac{\sqrt{6}\cdot \sqrt{3}}{3}=\sqrt{2}$，

$\therefore $ 在$\text{Rt}\triangle AHO$中，$AH=\sqrt{A{{O}^{2}}-O{{H}^{2}}}=\sqrt{{{(\sqrt{3})}^{2}}-{{(\sqrt{2})}^{2}}}=1$，

$\because OA=O{{A}_{1}}=R$，$O H \perp P A$，

$\therefore H$为线段$A{{A}_{1}}$的中点，

$\therefore A{{A}_{1}}=2AH=2$，

$\therefore P{{A}_{1}}=1$，

依题意，多面体${{A}_{1}}{{B}_{1}}{{C}_{1}}-ABC$为正三棱台，

$\therefore\dfrac{V_{P-A_1B_{1}C_{1}}}{V_{P-ABC}}=\left( \dfrac{PA_{1}}{PA}\right)^{3}=\dfrac{1}{27}$，即$V_{P-A_1B_{1}C_{1}}=\dfrac{1}{27}V_{P-ABC}$，

又${{V}_{P-ABC}}=\dfrac{1}{3}{{S}_{\triangle ABC}}\cdot PO=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{4}\times 9\times \sqrt{6}=\dfrac{\text{9}\sqrt{2}}{4}$，

$\therefore $ 正三棱台${{A}_{1}}{{B}_{1}}{{C}_{1}}-ABC$的体积为$V_{P-ABC}-V_{P-A_1B_{1}C_{1}}=\dfrac{26}{27}V_{P-ABC}=\dfrac{13\sqrt{2}}{6}$．

故答案为：$\dfrac{13\sqrt{2}}{6}$