半径为$R$的球的内接正三棱柱的侧面积（各侧面面积之和）的最大值为                 ．

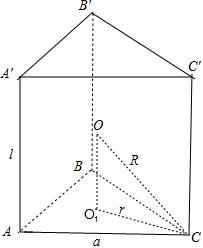
设正三棱柱的底面边长为$a$，侧棱长为$l$，

则底面圆半径为$r=\dfrac{\sqrt{3}}{3}a$，且${{\left(\dfrac{l}{2}\right)}^{2}}+{{r}^{2}}={{R}^{2}}$，

$\therefore {{l}^{2}}=4{{R}^{2}}-\dfrac{4}{3}{{a}^{2}}$，即$l=2\sqrt{{{R}^{2}}-\dfrac{{{a}^{2}}}{3}}$；

$\therefore $ 侧面积之和为${{S}_{侧}}=3al=6a\sqrt{{{R}^{2}}-\dfrac{{{a}^{2}}}{3}}=6\sqrt{3\cdot \dfrac{{{a}^{2}}}{3}\cdot \left({{R}^{2}}-\dfrac{{{a}^{2}}}{3}\right)} \leqslant 6\sqrt{3\cdot {{\left( \dfrac{\dfrac{{{a}^{2}}}{3}+{{R}^{2}}-\dfrac{{{a}^{2}}}{3}}{2} \right)}^{2}}}=3\sqrt{3}{{R}^{2}}$．

即半径为$R$的球内接正三棱柱的三个侧面积之和的最大值是$3\sqrt{3}{{R}^{2}}$．

故答案为：$3\sqrt{3}{{R}^{2}}$