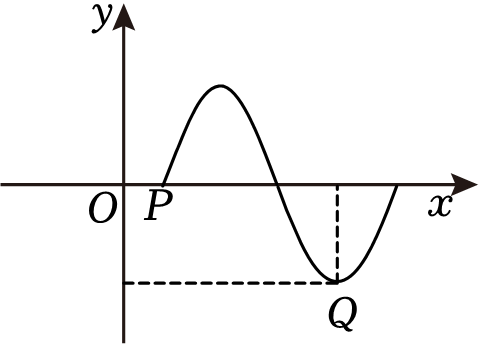
函数$f(x)=A\sin (\omega x+\varphi )\left(A\gt 0,\omega \gt 0,\vert \varphi \vert \lt \dfrac{\pi }{2}\right)$的部分图象如图，$P\left(\dfrac{2}{3},0\right)$和$Q\left(\dfrac{11}{3},-\sqrt{3}\right)$均在函数$f(x)$的图象上，且$Q$是图象上的最低点．

$(1)$求函数$f(x)$的单调递增区间；

$(2)$若$f(x_{0})=\dfrac{4\sqrt{3}}{5}$，$x_{0}\in \left[\dfrac{5}{3},\dfrac{8}{3}\right]$，求$\cos \dfrac{\pi x_0}{2}$的值．

$(1)$$\\left[-\\dfrac{1}{3}+4k,\\dfrac{5}{3}+4k\\right]$，$k\\in \\bf Z$；

$(2)$$-\\dfrac{3+4\\sqrt{3}}{10}$

$(1)$由题得，$A=\sqrt{3}$，$\dfrac{3}{4}T=3$，

故$T=4$，$\omega =\dfrac{\pi }{2}$，

由$f\left(\dfrac{11}{3}\right)=-\sqrt{3}$，得$\dfrac{\pi }{2}\times \dfrac{11}{3}+\varphi =\dfrac{3\pi }{2}+2k\pi$，$k\in {\bf Z}$，

故$\varphi =-\dfrac{\pi }{3}+2k\pi$，$k\in {\bf Z}$，$\vert \varphi \vert \lt \dfrac{\pi }{2}$，

故$\varphi =-\dfrac{\pi }{3}$，$f(x)=\sqrt{3}\sin \left(\dfrac{\pi }{2}x-\dfrac{\pi }{3}\right)$，

令$-\dfrac{\pi }{2}+2k\pi \leqslant \dfrac{\pi }{2}x-\dfrac{\pi }{3}\leqslant \dfrac{\pi }{2}+2k\pi \Rightarrow -\dfrac{1}{3}+4k\leqslant x\leqslant \dfrac{5}{3}+4k$，

即$f(x)$单调递增区间为$\left[-\dfrac{1}{3}+4k,\dfrac{5}{3}+4k\right]$，$k\in {\bf Z}$；

$(2)$由$f(x_0)=\dfrac{4\sqrt{3}}{5}$，即$\sin \left(\dfrac{\pi }{2}x_0-\dfrac{\pi }{3}\right)=\dfrac{4}{5}$，

又$x_0\in \left[\dfrac{5}{3},\dfrac{8}{3}\right]$，则$\left(\dfrac{\pi }{2}x_0-\dfrac{\pi }{3}\right)\in \left(\dfrac{\pi }{2},\pi \right)$，

故$\cos \left(\dfrac{\pi }{2}x_0-\dfrac{\pi }{3}\right)=-\dfrac{3}{5}$，

$\cos \left(\dfrac{\pi }{2}x_{0}\right)=\cos \left[\left(\dfrac{\pi }{2}x_{0}-\dfrac{\pi }{3}\right)+\dfrac{\pi }{3}\right]=\cos \left(\dfrac{\pi }{2}x_{0}-\dfrac{\pi }{3}\right)\cdot \dfrac{1}{2}-\sin \left(\dfrac{\pi }{2}x_{0}-\dfrac{\pi }{3}\right)\cdot \dfrac{\sqrt{3}}{2}=-\dfrac{3+4\sqrt{3}}{10}$．