如图，$ABCD$是一块边长为$100$米的正方形地皮，其中$ATS$是一座半径为$90$米的扇形小山，$P$是弧$TS$上一点，其余部分都是平地．现有一开发商想在平地上建造一个两边分别落在$BC$与$CD$上的长方形停车场$PQCR$，求长方形停车场$PQCR$面积的最大值．

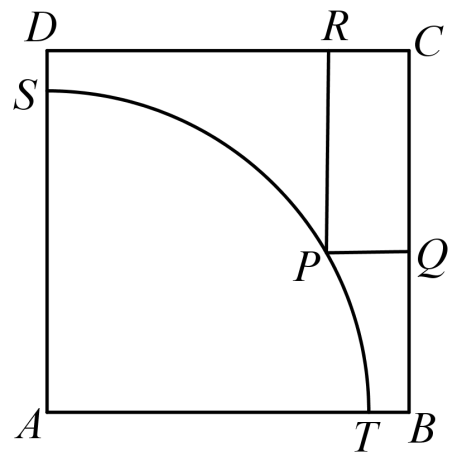
$14050-9000\\sqrt{2}(\\rm m^{2})$

如图，连接$AP$，

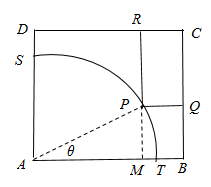
设$\angle PAB=\theta \left( 0\leqslant \theta \leqslant \dfrac{\pi}{2} \right)$，延长$RP$交$AB$于$M$，

则$AM=90\cos \theta $，$MP=90\sin \theta $，

$∴PQ=MB=AB-AM=100-90\cos \theta $，$PR=MR-MP=100-90\sin \theta $．

$∴$矩形$PQCR$的面积为

$S\left( \theta \right)=PQ\cdot PR=\left( 100-90\cos \theta \right)\left( 100-90\sin \theta \right)=10000-9000\left( \sin \theta +\cos \theta \right)+8100\sin \theta \cos \theta $

设$\sin \theta +\cos \theta =t\left( 1\leqslant t\leqslant \sqrt{2} \right)$，则$\sin \theta \cos \theta =\dfrac{1}{2}\left( {{t}^{2}}-1 \right)$，

$∴S\left( \theta \right)=10000-9000t+8100\times \dfrac{1}{2}\left( {{t}^{2}}-1 \right)=\dfrac{8100}{2}{{\left( t-\dfrac{10}{9} \right)}^{2}}+950$，

$∴$当$t=\sqrt{2}$时，$S{{\left( \theta \right)}_{\max }}=14050-9000\sqrt{2}\left( {{\rm m}^{2}} \right)$，

故长方形停车场$PQCR$面积的最大值是$14050-9000\sqrt{2}\left( {{\rm m}^{2}} \right)$．