人脸识别技术在各行各业的应用改变着人类的生活，所谓人脸识别，就是利用计算机分析人脸视频或者图像，并从中提取出有效的识别信息，最终判别对象的身份，人脸识别中检测样本之间的相似度主要应用距离的测试，常用测量距离的方式有曼哈顿距离和余弦距离．若二维空间有两个点$A\left(x_1, y_1\right)$，$ B\left(x_2, y_2\right)$，则曼哈顿距离为$d(A,B)=\left| {{x}_{1}}-{{x}_{2}} \right|+\left| {{y}_{1}}-{{y}_{2}} \right|$，余弦相似度为$\cos (A, B)=\dfrac{x_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}} \cdot \dfrac{x_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}+\dfrac{y_{1}}{\sqrt{x_{1}^{2}+y_{1}^{2}}} \cdot \dfrac{y_{2}}{\sqrt{x_{2}^{2}+y_{2}^{2}}}$，余弦距离为$1-\cos (A,B)$．

$(1)$若$A(-1,2)$，$B\left( \dfrac{3}{5},\dfrac{4}{5} \right)$，求$AB$之间的曼哈顿距离$d(A,B)$和余弦距离；

$(2)$已知$0\lt\alpha\lt\beta\lt\dfrac{\pi}{2}$，$E(5\cos\alpha,5\sin\alpha)$，$ F(13 \cos \beta, 13 \sin \beta)$，$P(5\cos(\alpha+\beta),5\sin(\alpha+\beta))$，若$\cos (E, P)=\dfrac{5}{13}$，$ \cos (E, F)=\dfrac{63}{65}$．

①求$d(E,F)$；

②若动点$G$满足$d(E, G)=d(E, F)$，求$G$围成封闭图形的面积．

$(1)$$d\\left( A,B \\right)=\\dfrac{14}{5}$，余弦距离为$\\dfrac{5-\\sqrt{5}}{5}$；

$(2)$①$d(E,F)=10$；②$200$

$(1)$$d(A,B)=\left| -1-\dfrac{3}{5} \right|+\left| 2-\dfrac{4}{5} \right|=\dfrac{14}{5},\cos (A,B)=-\dfrac{1}{\sqrt{5}}\times \dfrac{3}{5}+\dfrac{2}{\sqrt{5}}\times \dfrac{4}{5}=\dfrac{\sqrt{5}}{5}$；

故余弦距离为$1-\cos (A, B)=\dfrac{5-\sqrt{5}}{5}$；

$(2)$①$\because\sqrt{(5\sin\alpha)^{2}+(5\cos\alpha)^{2}}=5$，$\sqrt{[5\sin(\alpha+\beta)]^{2}+[5\cos(\alpha+\beta)]^{2}}=5$；

$\therefore\cos(E,P)=\dfrac{5\cos\alpha}{5}\cdot\dfrac{5\cos(\alpha+\beta)}{5}+\dfrac{5\sin\alpha}{5}\cdot\dfrac{5\sin(\alpha+\beta)}{5}=\cos\beta=\dfrac{5}{13}$；

$\because 0\lt \beta \lt \dfrac{\pi}{2}$，

$\therefore \sin \beta =\dfrac{12}{13}$；

$\therefore F(5,12)$；

$\therefore \cos (E, F)=\dfrac{5 \cos \alpha}{5} \cdot \dfrac{13 \cos \beta}{13}+\dfrac{5 \sin \alpha}{5} \cdot \dfrac{13 \sin \beta}{13}=\cos (\alpha-\beta)=\dfrac{63}{65}$；

$\because0\lt\alpha\lt\beta\lt\dfrac{\pi}{2}$，则$\alpha-\beta\in\left( -\dfrac{\pi}{2},0\right)$

$\therefore \sin (\alpha-\beta)=-\dfrac{16}{65}$；                                                                                                                                       

$\because\cos\alpha=\cos(\alpha-\beta+\beta)=\cos(\alpha-\beta)\cos\beta-\sin(\alpha-\beta)\sin\beta=\dfrac{3}{5}$；

$\therefore\sin\alpha=\dfrac{4}{5}$，即$E(3,4)$，$ d(E, F)=|3-5|+|4-12|=10$；

②$G\left( x,y \right)$，则$d(E,G)=\left| x-3 \right|+\left| y-4 \right|=10$，

$\therefore $ 动点$G$围成的封闭图形是正方形，如图所示：

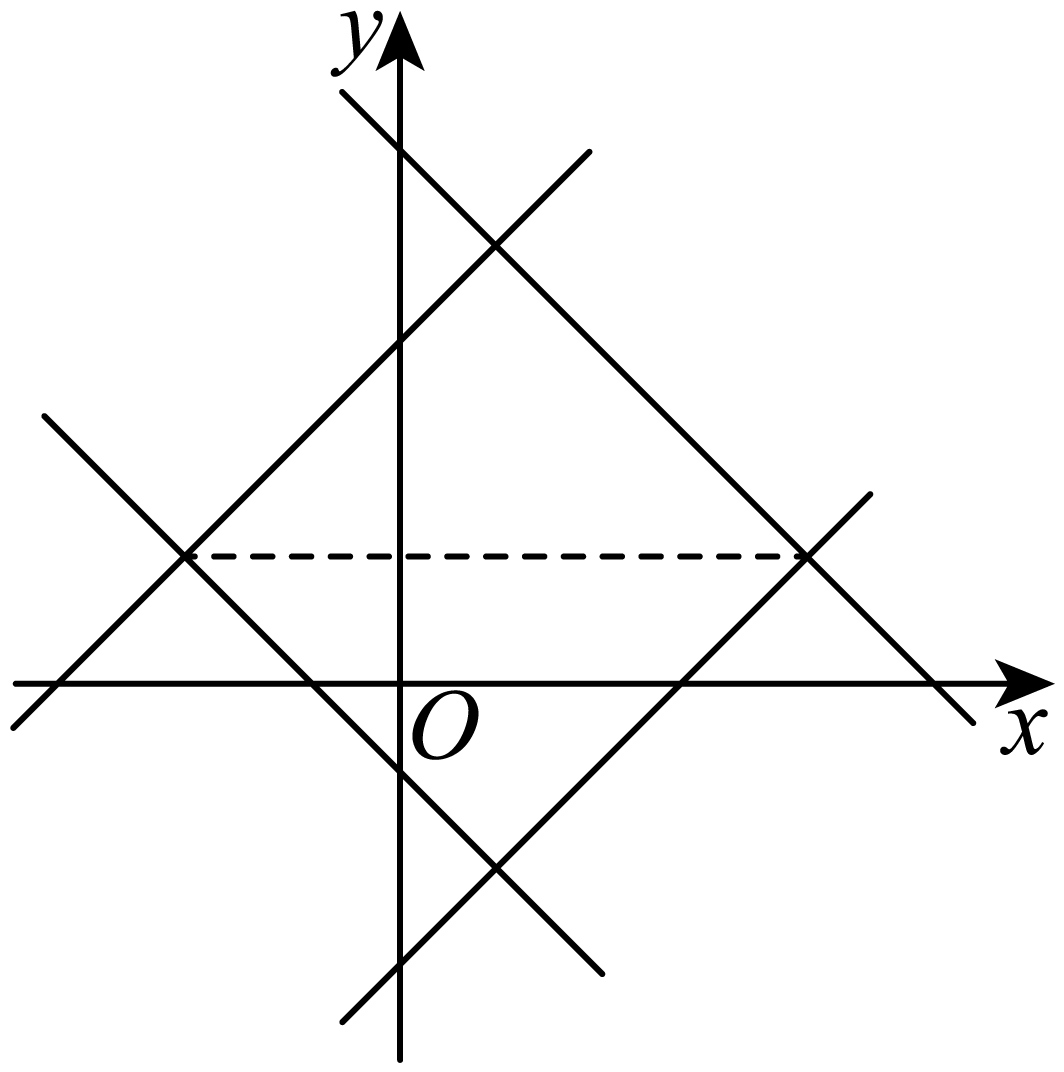
其边长为$10\sqrt{2}$，故围成的面积为$200$．