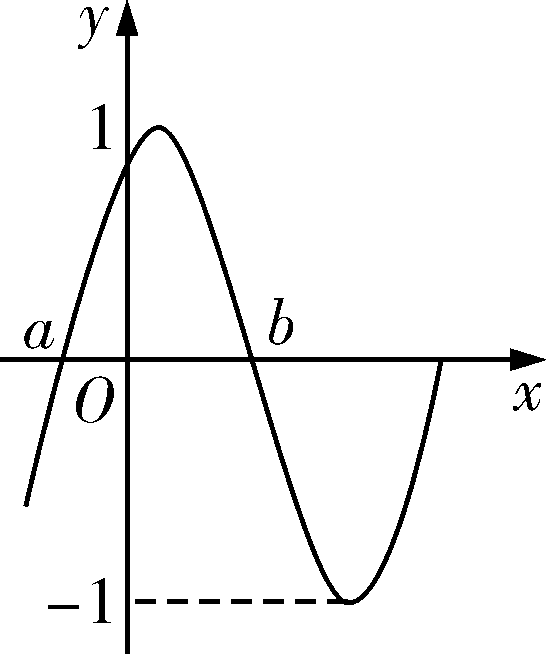
将函数$f\left( x \right)$的图象横坐标伸长为原来的$2$倍，再向左平移$\dfrac{\pi }{3}$个单位，得到函数$g\left( x\right)=\sin\left( 2x+\varphi\right)\left( 0\lt\varphi\lt\dfrac{\pi}{2}\right)$的部分图象（如图所示）．对于$\forall {{x}_{1}}$，${{x}_{2}}\in \left[ a,b \right]$，且${{x}_{1}}\ne {{x}_{2}}$，若$g\left( {{x}_{1}} \right)=g\left( {{x}_{2}} \right)$，都有$g\left( {{x}_{1}}+{{x}_{2}} \right)=\dfrac{\sqrt{3}}{2}$成立，则$(\qquad)$．

$g\\left( x \\right)=\\sin \\left( 2x+\\dfrac{\\pi }{3} \\right)$

$f\\left( x \\right)=\\sin \\left( 4x-\\dfrac{\\pi }{3} \\right)$

$g\\left( x \\right)$在$\\left[ \\pi ,\\dfrac{3\\pi }{2} \\right]$上单调递增

函数$f\\left( x \\right)$在$\\left[ 0,\\dfrac{4\\pi }{3} \\right]$的零点为${{x}_{1}}$，${{x}_{2}}$，$\\cdots $，${{x}_{n}}$，则${{x}_{1}}+2{{x}_{2}}+2{{x}_{3}}+\\cdot \\cdot \\cdot +2{{x}_{n-1}}+{{x}_{n}}=\\dfrac{85\\pi }{12}$

对于$\rm A$，由题意可知函数$g\left( x \right)=\sin \left( 2x+\varphi \right)\left( 0\lt \varphi \lt \dfrac{\pi }{2} \right)$的图象在区间$\left[ a,b \right]$上的对称轴为直线$x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$，又$g\left( {{x}_{1}}+{{x}_{2}} \right)=\dfrac{\sqrt{3}}{2}$，

$\therefore g\left( 0 \right)=g\left( {{x}_{1}}+{{x}_{2}} \right)=\dfrac{\sqrt{3}}{2}$，

$\therefore \sin \varphi =\dfrac{\sqrt{3}}{2}$，

$0\lt \varphi \lt \dfrac{\pi }{2}$，$\varphi =\dfrac{\pi }{3}$，故$g\left( x \right)=\sin \left( 2x+\dfrac{\pi }{3} \right)$，$\rm A$正确；

对于$\rm B$，$g\left( x \right)=\sin \left( 2x+\dfrac{\pi }{3} \right)$右移$\dfrac{\pi }{3}$个单位得到函数$y=\sin \left( 2x-\dfrac{\pi }{3} \right)$的图象，再将其横坐标缩短为原来的$\dfrac{1}{2}$得到$f\left( x \right)=\sin \left( 4x-\dfrac{\pi }{3} \right)$的图象，故$\rm B$正确；

对于$\rm C$，令$-\dfrac{\pi }{2}+2k\pi \leqslant 2x+\dfrac{\pi }{3}\leqslant \dfrac{\pi }{2}+2k\pi $，$k\in \bf{Z}$，得$-\dfrac{5\pi }{12}+k\pi \leqslant x\leqslant \dfrac{\pi }{12}+k\pi $，$k\in \bf{Z}$，当$k=1$时，$\dfrac{7\pi }{12}\leqslant x\leqslant \dfrac{13\pi }{12}$，

$\therefore g\left( x \right)$在$\left[ \dfrac{7\pi }{12},\dfrac{13\pi }{12} \right]$上单调递增，而$\left[ \pi ,\dfrac{3\pi }{2} \right]\varsubsetneq \left[ \dfrac{7\pi }{12},\dfrac{13\pi }{12} \right]$，故$\rm C$错误，

对于$\rm D$，令$t=4x-\dfrac{\pi }{3}$，则$t\in \left[ -\dfrac{\pi }{3},5\pi \right]$，函数$y=\sin t$在$\left[ -\dfrac{\pi }{3},5\pi \right]$上有$6$个零点${{t}_{1}}$，${{t}_{2}}$，$\cdots $，${{t}_{6}}$，则${{t}_{1}}+{{t}_{2}}=\pi $，${{t}_{2}}+{{t}_{3}}=3\pi $，${{t}_{3}}+{{t}_{4}}=5\pi $，${{t}_{4}}+{{t}_{5}}=7\pi $，${{t}_{5}}+{{t}_{6}}=9\pi $，

故${{t}_{1}}+2{{t}_{2}}+2{{t}_{3}}+2{{t}_{4}}+2{{t}_{5}}+{{t}_{6}}=4\left( {{x}_{1}}+2{{x}_{2}}+2{{x}_{3}}+2{{x}_{4}}+2{{x}_{5}}+{{x}_{6}} \right)-10\times \dfrac{\pi }{3}=25\pi $，

$\therefore {{x}_{1}}+2{{x}_{2}}+2{{x}_{3}}+\cdots +2{{x}_{n-1}}+{{x}_{n}}=\dfrac{85}{12}\pi $，故$\rm D$正确．

故选：$\rm ABD$