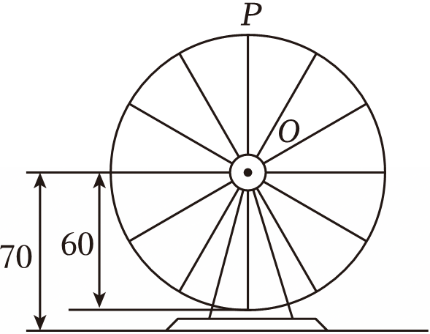
如图，摩天轮的半径为$60\;\rm m$，点$O$距地面的高度为$70\;\rm m$，摩天轮按逆时针方向匀速转动，每$18\;\rm min$转一圈，若摩天轮上点$P$的起始位置在最高点处，则在摩天轮转动的过程中，$(\qquad)$．

转动$9\\;\\rm min$后点$P$距离地面$8\\;\\rm m$

第$16\\;\\rm min$和第$38\\;\\rm min$点$P$距离地面的高度相同

转速减半时转动一圈所需的时间变为原来的$\\dfrac{1}{2}$

转动一圈内，点$P$距离地面的高度不低于$100\\;\\rm m$的时长为$5.5\\;\\rm min$

设函数$y=A\sin (\omega x+\varphi )+B$，则$A=60$，$B=70$，$T=18$，

$\therefore \omega =\dfrac{2\pi }{T}=\dfrac{\pi }{9}$，

$x=0$时，$60\sin \varphi +70=130$，

$\therefore \sin \varphi =1$，

$\therefore \varphi =\dfrac{\pi }{2}+2k\pi$，$k\in {\bf Z}$；

$\therefore y=60\sin \left(\dfrac{\pi }{9}x+\dfrac{\pi }{2}\right)+70$．

$x=9$时，$y=60\sin \left(\dfrac{\pi }{9}\times 9+\dfrac{\pi }{2}\right)+70=10$，点$P$距离地面$10\;\rm m$，选项$\rm A$错误；

$x=16$时，$y=60\sin \left(\dfrac{\pi }{9}\times 16+\dfrac{\pi }{2}\right)+70=60\cos \dfrac{2\pi }{9}+70$，

$x=38$时，$y=60\sin \left(\dfrac{\pi }{9}\times 38+\dfrac{\pi }{2}\right)+70=60\cos \dfrac{2\pi }{9}+70$，点$P$距离地面的高度相同，选项$\rm B$正确；

转速减半时转动一圈所需的时间变为原来的$2$倍，选项$\rm C$错误；

令$y\geqslant 0$，得$60\sin \left(\dfrac{\pi }{9}x+\dfrac{\pi }{2}\right)+70\geqslant 100$，得$\cos \dfrac{\pi }{9}x\leqslant \dfrac{1}{2}$，解得$-\dfrac{\pi }{3}\leqslant \dfrac{\pi }{9}x\leqslant \dfrac{\pi }{3}$，

即$-3\leqslant x\leqslant 3$，

$\therefore $ 点$P$距离地面的高度不低于$100\;\rm m$的时长为$6\;\rm min$，选项$\rm D$错误．

故选：$\rm B$