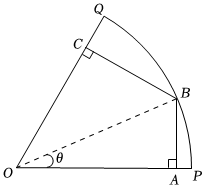
如图，扇形钢板$POQ$的半径为$1m$，圆心角为$60^{\circ}$.现要从中截取一块四边形钢板$ABCO$.其中顶点$B$在扇形$POQ$的弧$\widehat {PQ}$上，$A$，$C$分别在半径$OP$，$OQ$上，且$AB\bot OP$，$BC\bot OQ$.
$(1)$设$\angle AOB=\theta $，试用$\theta $表示截取的四边形钢板$ABCO$的面积$S\left(\theta \right)$，并指出$\theta $的取值范围；
$(2)$求当$\theta $为何值时，截取的四边形钢板$ABCO$的面积最大.

$(1)$$S(\\theta )=\\dfrac{1}{4}[\\sin2\\theta +\\sin(\\dfrac{{2\\pi }}{3}-2\\theta )]$，$\\theta ∈(0,\\dfrac{\\pi }{3})$

$(2)$$\\theta =\\dfrac{\\pi }{6}$时，$\\dfrac{{\\sqrt{3}}}{4}{m^2}$$.$

$(1)$因为$\angle AOB=\theta $，扇形钢板$POQ$的圆心角为$60^{\circ}$，所以$∠BOC=\dfrac{\pi }{3}-\theta $，
因为扇形钢板$POQ$的半径为$1m$，$AB\bot OP$，$BC\bot OQ$，
所以$OA=\cos \theta $，$AB=\sin \theta $，
所以${S_{△OAB}}=\dfrac{1}{2}OA\cdot AB=\dfrac{1}{2}\sin\theta \cos\theta =\dfrac{1}{4}\sin2\theta $，
又$OC=\cos(\dfrac{\pi }{3}-\theta )$，$BC=\sin(\dfrac{\pi }{3}-\theta )$，
所以${S_{△OBC}}=\dfrac{1}{2}OC\cdot BC=\dfrac{1}{2}\cos(\dfrac{\pi }{3}-\theta )\sin(\dfrac{\pi }{3}-\theta )=\dfrac{1}{4}\sin(\dfrac{{2\pi }}{3}-2\theta )$，
所以四边形钢板$ABCO$的面积$S(\theta )={S_{△OAB}}+{S_{△OBC}}=\dfrac{1}{4}[\sin2\theta +\sin(\dfrac{{2\pi }}{3}-2\theta )]$，$\theta ∈(0,\dfrac{\pi }{3})$，
其中$\theta $的取值范围为$(0,\dfrac{\pi }{3})$.
$(2)S(\theta )=\dfrac{1}{4}[\sin2\theta +\sin(\dfrac{{2\pi }}{3}-2\theta )]=\dfrac{1}{4}(\sin2\theta +\dfrac{{\sqrt{3}}}{2}\cos2\theta +\dfrac{1}{2}\sin2\theta )=\dfrac{1}{4}(\dfrac{3}{2}\sin2\theta +\dfrac{{\sqrt{3}}}{2}\cos2\theta )=\dfrac{{\sqrt{3}}}{4}(\dfrac{{\sqrt{3}}}{2}\sin2\theta +\dfrac{1}{2}\cos2\theta )=\dfrac{{\sqrt{3}}}{4}\sin(2\theta +\dfrac{\pi }{6})$，
因为$\theta ∈(0,\dfrac{\pi }{3})$，所以$2\theta +\dfrac{\pi }{6}∈(\dfrac{\pi }{6},\dfrac{{5\pi }}{6})$，
所以当$2\theta +\dfrac{\pi }{6}=\dfrac{\pi }{2}$，即$\theta =\dfrac{\pi }{6}$时，四边形钢板$ABCO$的面积$S\left(\theta \right)$最大，最大值为$\dfrac{{\sqrt{3}}}{4}{m^2}$.