| 1.8 三角函数的简单应用 题目答案及解析
稿件来源:高途
| 1.8 三角函数的简单应用题目答案及解析如下,仅供参考!
必修二
第一章 三角函数
1.8 三角函数的简单应用
从秦朝统一全国币制到清朝末年,圆形方孔铜钱(简称“孔方兄”$) $是我国使用时间长达两千多年的货币.如图$1$,这是一枚清朝同治年间的铜钱,其边框是由大小不等的两同心圆围成的,内嵌正方形孔的中心与同心圆圆心重合,正方形外部,圆框内部刻有四个字“同治重宝”.某模具厂计划仿制这样的铜钱作为纪念品,其小圆内部图纸设计如图$2$所示,小圆直径$1$厘米,内嵌一个大正方形孔,四周是四个全等的小正方形(边长比孔的边长小),每个正方形有两个顶点在圆周上,另两个顶点在孔边上,四个小正方形内用于刻铜钱上的字.设$\angle OAB=\theta $,五个正方形的面积和为$S$.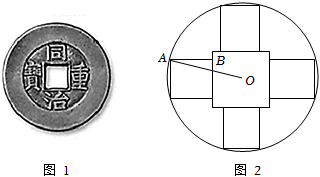
$(1)$求面积$S$关于$\theta $的函数表达式,并求$\tan \theta $的范围;
$(2)$求面积$S$最小值.
答案见解析
"]]$(1)$过点$O$分别作小正方形边,大正方形边的垂线,垂足分别为$E$,$F$,
因为内嵌一个大正方形孔的中心与同心圆圆心重合,
所以点$E$,$F$分别为小正方形和大正方形边的中点,
所以小正方形的边长为$(\dfrac{1}{2}\sin\theta )×2=\sin\theta $,
大正方形的边长为$(\dfrac{1}{2}\cos\theta -\sin\theta )×2=\cos\theta -2\sin\theta $,
所以五个正方形的面积和为$S=4\sin ^{2}\theta +\left(\cos \theta -2\sin \theta \right)^{2}=8\sin ^{2}\theta +\cos ^{2}\theta -4\sin \theta \cos \theta $,
因为小正方形边长小于内嵌一个大正方形的边长,
所以$\sin \theta\ \ \lt \cos \theta -2\sin \theta $,所以$tan\theta \lt \dfrac{1}{3}$,
所以$\theta $的取值范围为$(0$,$\theta _{0}$$)$,$\tan{\theta }_{0}=\dfrac{1}{3}$,${\theta }_{0}∈(0,\dfrac{\pi }{2})$;
$(2)S=8\sin ^{2}\theta +\cos ^{2}\theta -4\sin \theta \cos \theta =\dfrac{8{\sin}^{2}\theta +co{s}^{2}\theta -4\sin\theta \cos\theta }{{\sin}^{2}\theta +{\cos}^{2}\theta }=\dfrac{8{\tan}^{2}\theta -4tan\theta +1}{{\tan}^{2}\theta +1}$,
令$t=\tan \theta $,则$S=\dfrac{8{t}^{2}-4t+1}{{t}^{2}+1}$,设$f\left(t\right)=\dfrac{8{t}^{2}-4t+1}{{t}^{2}+1}$,$t∈(0,\dfrac{1}{3})$,
令${f}{'}\left(t\right)=\dfrac{2(2{t}^{2}+7t-2)}{({t}^{2}+1)^{2}}=0$得:$t=\dfrac{-7+\sqrt{65}}{4}\lt \dfrac{1}{3}$,
| $t$ | $(0$,$\dfrac{-7+\sqrt{65}}{4})$ | $\dfrac{-7+\sqrt{65}}{4}$ | $(\dfrac{-7+\sqrt{65}}{4}$,$\dfrac{1}{3})$ |
| ${f'}\left(t\right)$ | $-$ | $0$ | $+$ |
| $f\left(t\right)$ | 递减 | 极小值 | 递增 |
所以$t=\dfrac{-7+\sqrt{65}}{4}$时,面积$S$最小值为$\dfrac{9-\sqrt{65}}{2}$,
答:面积$S$最小值为$\dfrac{9-\sqrt{65}}{2}$.
| 1.8 三角函数的简单应用题目答案及解析(完整版)
