| 4.3.1 一元线性回归模型 题目答案及解析
稿件来源:高途
| 4.3.1 一元线性回归模型题目答案及解析如下,仅供参考!
选择性必修二
第四章 概率与统计
4.3 统计模型
4.3.1 一元线性回归模型
从传统旅游热点重现人山人海场面,到新兴旅游城市异军突起;从“特种兵式旅游”出圈,到“味蕾游”兴起;从文博演艺一票难求,到国风国潮热度不减$\cdots \cdots 2023$年“五一”假期旅游市场传递出令人振奋的信息.这个“五一”假期,您在游玩时的满意度如何?您对景区在“吃住行游购娱”等方方面面有哪些评价和感受?为此,某市文旅局对市内各景区进行了游客满意度测评(满分$100$分$)$.
$(1)$本市一景区随机选取了$100$名游客的测评成绩作为样本并进行统计,得到如表频率分布表.
| 成绩 | $\left[0,20\right)$ | $\left[20,40\right)$ | $\left[40,60\right)$ | $\left[60,80\right)$ | $\left[80,100\right]$ |
| 频率 | $0.1$ | $0.1$ | $0.3$ | $0.35$ | $0.15$ |
按照分层抽样的方法,先从样本测评成绩在$\left[0,20\right)$,$\left[80,100\right]$的游客中随机抽取$5$人,再从这$5$人中随机选取$3$人赠送纪念品,记这$3$人中成绩在$\left[80,100\right]$的人数为$X$,求$X$的分布列及期望;
$(2)$该市文旅局规定游客满意度测评成绩在$80$分及以上为“好评”,并分别统计了该市$7$个景区满意度测评的平均成绩$x$与“好评”率$y$,如表所示:
| $x$ | $32$ | $41$ | $54$ | $68$ | $74$ | $80$ | $92$ |
| $y$ | $0.28$ | $0.34$ | $0.44$ | $0.58$ | $0.66$ | $0.74$ | $0.94$ |
根据数据初步判断,可选用$y=k{\rm e}^{\lambda x}(k\gt0)$作为回归方程.
求该回归方程;
$(ii)$根据以上统计分析,可以认为本市各景区满意度测评平均成绩$x\sim N\left(\mu ,400\right)$,其中$\mu $近似为样本平均数$a$,估计该市景区“好评”率不低于$0.78$的概率为多少?
参考公式与数据:
①若$z=\ln y$,则$\overline{z}\approx -0.64$,$\dfrac{\sum_{i=1}^{7}{x}_{i}{z}_{i}-7\overline{x}\overline{z}}{\sum_{i=1}^{n}{x}_{i}^{2}-7{\overline{x}}^{2}}\approx 0.02$,$\ln 0.15\approx -1.9$,$\ln 5.2\approx 1.66$.
②线性回归方程$\hat{y}=\hat{b}x+\hat{a}$中,$\hat{b}=\dfrac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\hat{a}=\overline{y}-\hat{b}\overline{x}$.
③若随机变量$X\sim N(u,\sigma ^{2})$,则$P\left( \mu-\sigma\lt X\lt\mu+\sigma\right)\approx0.683$;
$P\left(\mu -2\sigma\ \ \lt X \lt \mu +2\sigma \right)\approx 0.954$;
$P\left(\mu -3\sigma\ \ \lt X \lt \mu +3\sigma \right)\approx 0.997$.
$(1)$答案见解析;
$(2)$$(i)$$y=0.15{\\rm e}^{0.02x}$;
$(ii)$$0.1585$
"]]$(1)$按照分层抽样的方法,测评成绩在$\left[0,20\right)$的游客有$2$人,$\left[80,100\right]$的游客有$3$人,则$X$的取值范围是$\{1,2,3\}$,
$P(X=1)=\dfrac{{\rm C}_{3}^{1}{\rm C}_{2}^{2}}{{\rm C}_{5}^{3}}=0.3$,$P(X=2)=\dfrac{{\rm C}_{3}^{2}{\rm C}_{2}^{1}}{{\rm C}_{5}^{3}}=0.6$,$P(X=3)=\dfrac{{\rm C}_{3}^{3}{\rm C}_{2}^{0}}{{\rm C}_{5}^{3}}=0.1$,
$X$分布列为;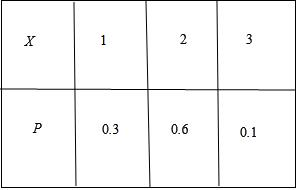 $E\left( X\right)=1\times 0.3+2\times 0.6+3\times 0.1=1.8$.
$E\left( X\right)=1\times 0.3+2\times 0.6+3\times 0.1=1.8$.
$(2)\left(i\right)$对$\ \ y=k{\rm e}^{\lambda x}$两边取对数得$\ln y=\ln k+\lambda x$,令$z=\ln y$,则$z=\lambda x+\ln k$,
根据所给公式可得$\lambda =\dfrac{\sum_{i=1}^{7}{x}_{i}{z}_{i}-7\boldsymbol{x}\cdot \boldsymbol{z}}{\sum_{i=1}^{7}{x}_{i}^{2}-7{\boldsymbol{x}}^{2}}≈0.02$,
又$\because \overline{x}=\dfrac{32+41+54+68+74+80+92}{7}=63$,$\overline{z}≈-0.64$,
$\therefore \ln k=-0.64-0.02\times 63=-1.9$,即$k\approx 0.15$,
$\therefore $该回归方程为:$y=0.15{\rm e}^{0.02x}$;
$(ii)$由$\left(i\right)$及参考数据可得$\mu \approx \overline{x}=63$,$\sigma =20$,
由$y\geqslant 0.78$即$0.15{\rm e}^{0.02x}\geqslant0.78$可得$x\geqslant\dfrac{\ln5.2}{0.02}\approx83$,
又$\mu +\sigma =83$,$P\left( \mu-\sigma\lt x\lt\mu+\sigma\right)\approx0.683$,
由正态分布的性质得:
$P\left(x\geqslant 83\right)=P\left(x\leqslant 43\right)=\dfrac{1-0.683}{2}=0.1585$,
估计该市景区“好评”率不低于$0.78 $的概率为$0.1585$.
| 4.3.1 一元线性回归模型题目答案及解析(完整版)
