在四棱锥$P-ABCD$中，底面$ABCD$为正方形，$PA=AB=1$，$M$为空间中一动点，$G$为$PC$的中点，$PA\bot $平面$ABCD$.若$\overrightarrow{MA}\cdot \overrightarrow{MG}=0$，则$M$的轨迹围成封闭图形的体积为                  ；若$PC$与平面$PBA$所成的角等于$\angle AMG$，则平面$PBD$与$M$的轨迹的交线长为                  .

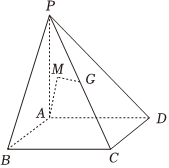
$\because \overrightarrow{MA}\cdot \overrightarrow{MG}=0$，$\therefore M$在以$AG$为直径的球面上，
$\therefore AG=\dfrac{1}{2}PC=\dfrac{1}{2}\sqrt{1+2}=\dfrac{\sqrt{3}}{2}$，$\therefore $球的半径$R=\dfrac{\sqrt{3}}{4}$，
$\therefore M$的轨迹围成封闭图形的体积为$V=\dfrac{4}{3}\pi \cdot \dfrac{3}{16}\times \dfrac{\sqrt{3}}{4}=\dfrac{\sqrt{3}\pi }{16}$；
$PC$与平面$PBA$所成的角为$\angle CPB$，$\therefore \tan \angle AMG=\tan \angle CPB=\dfrac{\sqrt{2}}{2}$，
$\therefore \sin \angle AMG=\dfrac{\sqrt{3}}{3}=\sin \theta $，且$AG\bot $平面$PBD$，$A$到直线$PBD$的距离为$\dfrac{\sqrt{3}}{3}$，
由$\angle AMG$为确定的锐角，$M$与$A$，$G$张角为定值，
$\therefore M$的轨迹为以$AG$为弦的球的上，下方合着的球冠，设球心为$O$，
连接$OA$，$OG$，过$O$作$ON\bot AG$于点$N$，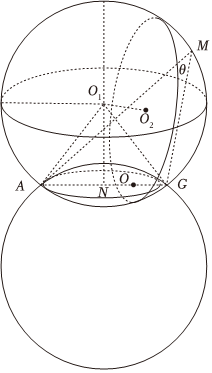
，
$\odot O_{2}$为平面$PBD$截球$O$的面，$AG\bot \odot O_{2}$交于$Q$点，
$\therefore NG=\dfrac{1}{2}AG=\dfrac{\sqrt{3}}{4}$，$NQ=\dfrac{\sqrt{3}}{3}-\dfrac{\sqrt{3}}{4}=\dfrac{\sqrt{3}}{12}=OO_{2}$，
设平面$PBD$与$M$的轨迹交线一侧所在圆$O_{2}$半径为$r$，
而大球$O$半径$R=\dfrac{NG}{\sin\theta}=\dfrac{\sqrt{3}}{4}\cdot\sqrt{3}=\dfrac{3}{4}$，$\therefore r=\sqrt{\dfrac{9}{16}-(\dfrac{\sqrt{3}}{12})^{2}}=\sqrt{\dfrac{13}{24}}$，
$O_{2}O=ON=\dfrac{\sqrt{6}}{4}$，
$\therefore $轨迹的交线长为：$\pi (\sqrt{\dfrac{13}{24}}+\dfrac{\sqrt{6}}{4})\cdot 2=\dfrac{\sqrt{78}+3\sqrt{6}}{6}\pi $.
故答案为：$\dfrac{\sqrt{3}\pi }{16}$；$\dfrac{\sqrt{78}+3\sqrt{6}}{6}\pi $.