已知圆锥侧面展开图是圆心角为直角，半径为$2$的扇形，则此圆锥内切球的表面积为$(\qquad)$．

$13\\pi$

$\\dfrac{52}{81}\\pi$

$\\dfrac{\\sqrt{15}}{50}\\pi$

$\\dfrac{3}{5}\\pi$

圆锥侧面展开图扇形的弧长为$2\times \dfrac{\pi }{2}=\pi$，

圆锥底面的半径$r$满足$2\pi r=\pi$，解得$r=\dfrac{1}{2}$，

$\therefore $ 该圆锥轴截面是一个两腰长为$2$，底边长为$1$的等腰三角形，底边上的高为$\dfrac{\sqrt{15}}{2}$，

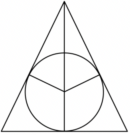
设此圆锥内切球半径为$R$，则$R(1+2+2)=1\times \dfrac{\sqrt{15}}{2}$，

解得$R=\dfrac{\sqrt{15}}{10}$．

$\therefore $ 内切球的表面积为$S=4\pi {R^2}=\dfrac{3}{5}\pi$．

故选：$\rm D$