已知在六面体$PABCDE$中，$PA\bot $平面$ABCD$，$ED\bot $平面$ABCD$，且$PA=2ED$，底面$ABCD$为菱形，且$\angle ABC=60^{\circ}$.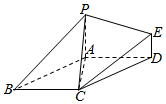
$(1)$求证：平面$PAC\bot $平面$PBD$；
$(2)$若直线$PC$与平面$ABCD$所成角为$45^{\circ}$，试问：在线段$PE$上是否存在点$M$，使二面角$P-AC-M$为$60^{\circ}$？若存在，确定点$M$的位置；若不存在，请说明理由.

(1) 证明见解析;

(2) 存在点$M$即为点$E$时，二面角$P - AC - M$为$60^{\\circ}$

$(1)$证明：连接$BD$，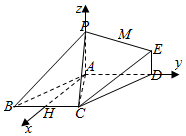
$\because $四边形$ABCD$为菱形，$\therefore BD\bot AC$，
又$PA\bot $平面$ABCD$，$BD\subset $平面$ABCD$，$\therefore BD\bot PA$，
又$PA\cap AC=A$，$\therefore BD\bot $平面$PAC$，
又$BD\subset $平面$PBD$，$\therefore $平面$PBD\bot $平面$PAC$；
$(2)$$\because PA\bot $平面$ABCD$，$\therefore AC$为$PC$在平面$ABCD$上的射影，
$\therefore \angle PCA$为直线$PC$与平面$ABCD$所成角，则$\angle PCA=45^{\circ}$，得$PA=AC$，
令$DE=1$，则$PA=AC=2$，
又四边形$ABCD$为菱形，$\angle ABC=60^{\circ}$，$\therefore \triangle ABC$为等边三角形，得$AB=2$，
取$BC$的中点$H$，连接$AH$，可得$AH=\sqrt{3}$，且$AH\bot BC$，$\therefore AH\bot AD$，
以$A$为原点，分别以$AH$，$AD$，$AP$所在直线为$x$，$y$，$z$，建立空间直角坐标系，
如图所示，，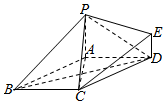
则$E\left(0,2,1\right)$，$P\left(0,0,2\right)$，$C(\sqrt{3},1,0)$，$B(\sqrt{3},-1,0)$，$D\left(0,2,0\right)$，
$\therefore \overrightarrow{EP}=(0,-2,1)$，设$M\left(x,y,z\right)$，
$\because M$，$P$，$E$三点共线，$\therefore \overrightarrow{EM}=\lambda \overrightarrow{EP}(0≤\lambda ≤1)$，则$\left(x,y-2,z-1\right)=\lambda \left(0,-2,1\right)$，
解得$x=0$，$y=2-2\lambda $，$z=1+\lambda $，$\therefore M\left(0,2-2\lambda ,1+\lambda \right)$，
$\therefore \overrightarrow{AC}=(\sqrt{3},1,0)$，$\overrightarrow{AM}=(0,2-2\lambda ,1+\lambda )$，$\overrightarrow{BD}=(-\sqrt{3},3,0)$，
由$(1)$知$BD\bot $平面$PAC$，$\therefore $平面$PAC$的法向量${\boldsymbol{n}_1}∥\overrightarrow{BD}$，取${\boldsymbol{n}_1}=(-1,\sqrt{3},0)$，
令平面$ACM$的法向量为${\boldsymbol{n}_2}=(x,y,z)$，
则$\left\{\begin{array}{l}{\boldsymbol{{n}_{2}}\cdot \overrightarrow{AC}=\sqrt{3}x+y=0}\\{\boldsymbol{{n}_{2}}\cdot \overrightarrow{AM}=(2-2\lambda )y+(1+\lambda )z=0}\end{array}\right.$，令$y=\sqrt{3}$，则${\boldsymbol{n}_2}=({-1,\sqrt{3},\dfrac{{2\sqrt{3}(\lambda -1)}}{{\lambda +1}}})$，
$\because $二面角$P-AC-M$为$60^{\circ}$，$\therefore |{\cos⟨{{{\boldsymbol{n}}_1},{{\boldsymbol{n}}_2}}⟩}|=|{\cos60°}|=\dfrac{{|{{{\boldsymbol{n}}_1}\cdot {{\boldsymbol{n}}_2}}|}}{{|{{{\boldsymbol{n}}_1}}∥{{{\boldsymbol{n}}_2}}|}}$，
$\therefore \dfrac{4}{{2\cdot \sqrt{4+\dfrac{{12{{(\lambda -1)}^2}}}{{{{(\lambda +1)}^2}}}}}}=\dfrac{1}{2}$，解得$\lambda =0$，
$\because 0\leqslant \lambda \leqslant 1$，$\therefore $当$\lambda =0$时，点$M$与点$E$重合，
$\therefore $存在点$M$即为点$E$时，二面角$P-AC-M$为$60^{\circ}$.