已知四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$如图所示，底面$ABCD$为平行四边形，其中点$D$在平面$A_{1}B_{1}C_{1}D_{1}$内的投影为点$A_{1}$，且$AB=AA_{1}=2AD,\angle ABC=120^{\circ}$.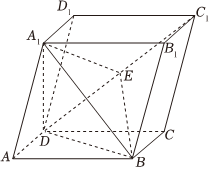
$(1)$求证：平面$A_{1}BD\bot $平面$ADD_{1}A_{1}$；
$(2)$已知点$E$在线段$C_{1}D$上（不含端点位置），且平面$A_{1}BE$与平面$BCC_{1}B_{1}$的夹角的余弦值为$\dfrac{\sqrt{5}}{5}$，求$\dfrac{DE}{E{C}_{1}}$的值.

$(1)$ 证明见解析
$(2)$ $\\dfrac{1}{3}$

$(1)$证明：四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$如图所示，底面$ABCD$为平行四边形，
点$D$在平面$A_{1}B_{1}C_{1}D_{1}$内的投影为点$A_{1}$，且$AB=AA_{1}=2AD,\angle ABC=120^{\circ}$.
$\because A_{1}D\bot $平面$ABCD$，$AD\subset $平面$ABCD$，$\therefore A_{1}D\bot AD$，
在$\triangle ADB$中，设$AB=2$，$AD=1$，$\angle DAB=60^{\circ}$，
由余弦定理，得$BD^{2}=AB^{2}+AD^{2}-2AB\cdot AD\cdot \cos \angle DAB=2^{2}+1^{2}-2\times 2\times 1\times \cos 60^{\circ}=3,\therefore BD=\sqrt{3}$，
$\therefore AD^{2}+BD^{2}=AB^{2}$，$\therefore AD\bot DB$.
$\because A_{1}D\cap DB=D$，$\therefore AD\bot $平面$A_{1}BD$，
$\because AD\subset $平面$ADD_{1}A_{1}$，$\therefore $平面$A_{1}BD\bot $平面$ADD_{1}A_{1}$.
$(2)$由$(1)$知，$DA$，$DB$，$DA_{1}$两两垂直，以$D$为坐标原点，
分别以向量$\overrightarrow{DA},\overrightarrow{DB}$，$\overrightarrow{D{A}_{1}}$的方向为$x$轴，$y$轴，$z$轴正方向，建立空间直角坐标系$D-xyz$，如图，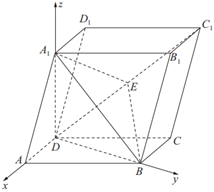
，
则$D\left(0,0,0\right),A\left(1,0,0\right)$，$B\left(0,\sqrt{3},0\right),{A}_{1}\left(0,0,\sqrt{3}\right),C\left(-1,\sqrt{3},0\right)$，
$\overrightarrow{AC}=\left(-2,\sqrt{3},0\right),A_{1}C_{1}=AC,\therefore {C}_{1}\left(-2,\sqrt{3},\sqrt{3}\right)$，
$\therefore \overrightarrow{{A}_{1}B}=\left(0,\sqrt{3},-\sqrt{3}\right),\overrightarrow{D{C}_{1}}=\left(-2,\sqrt{3},\sqrt{3}\right)$，
设$\overrightarrow{DE}=\lambda \overrightarrow{D{C}_{1}}\left(0\lt \lambda \lt 1\right)$，则$\overrightarrow{DE}=\lambda \overrightarrow{D{C}_{1}}=\left(-2\lambda ,\sqrt{3}\lambda ,\sqrt{3}\lambda \right)$，即$E\left(-2\lambda ,\sqrt{3}\lambda ,\sqrt{3}\lambda \right)$.
$\therefore \overrightarrow{{A}_{1}E}=\left(-2\lambda ,\sqrt{3}\lambda ,\sqrt{3}\lambda -\sqrt{3}\right)$；
设$\boldsymbol{n}=\left({x}_{1},{y}_{1},{z}_{1}\right)$为平面$A_{1}EB$的一个法向量，
则$\left\{\begin{array}{c}\boldsymbol{n}\cdot \overrightarrow{{A}_{1}B}=0\\ \boldsymbol{n}\cdot \overrightarrow{{A}_{1}E}=0\end{array}\right.$即$\left\{\begin{array}{c}\sqrt{3}{y}_{1}-\sqrt{3}{z}_{1}=0\\-2\lambda {x}_{1}+\sqrt{3}\lambda {y}_{1}+\left(\sqrt{3}\lambda -\sqrt{3}\right){z}_{1}=0\end{array}\right.$，
令$z_{1}=2\lambda $，得$\boldsymbol{n}=\left(2\sqrt{3}\lambda -\sqrt{3},2\lambda ,2\lambda \right)$；
由题意得知$DB\bot $平面$BCC_{1}B_{1}$，故$\boldsymbol{m}=\left(0,1,0\right)$为平面$BCC_{1}B_{1}$的一个法向量；
设平面$A_{1}EB$与平面$BCC_{1}B_{1}$的夹角为$\alpha $，
点$E$在线段$C_{1}D$上（不含端点位置），且平面$A_{1}BE$与平面$BCC_{1}B_{1}$的夹角的余弦值为$\dfrac{\sqrt{5}}{5}$，
则$\cos\alpha =\dfrac{|\boldsymbol n\cdot \boldsymbol m|}{|\boldsymbol n|\cdot |\boldsymbol m|}=\dfrac{2\lambda }{\sqrt{20{\lambda }^{2}-12\lambda +3}}=\dfrac{\sqrt{5}}{5}$，
解得$\lambda =\dfrac{1}{4}$，故$\dfrac{DE}{E{C}_{1}}=\dfrac{1}{3}$.