如图，函数$f(x)=A\sin\left(\omega x+\phi \right)\left(A\gt 0,\omega \gt 0,|\phi |≤\dfrac{\pi }{2}\right)$的图象与$x$轴的其中两个交点为$A$，$B$，与$y$轴交于点$C$，$D$为线段$BC$的中点，$OB=\sqrt{3}OC$，$OA=2$，$AD=\dfrac{2\sqrt{21}}{3}$，则$ $ $(\qquad)$ $ $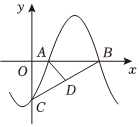

$f\\left(x\\right)$的最小正周期为$12\\pi $

$f\\left(x\\right)$的图象关于直线$x=8$对称

$f\\left(x\\right)$在$\\left[5,7\\right]$单调递减

$f\\left(-x+2\\right)$为奇函数

由题可$A\left(2,0\right),B\left(2+\dfrac{\pi }{\omega },0\right),C\left(0,A\sin \varphi \right)$，则$D\left(1+\dfrac{\pi }{2\omega },\dfrac{A\sin\phi }{2}\right)$，
有$\sqrt{3}|A\sin\phi |=2+\dfrac{\pi }{\omega },\sin \left(2\omega +\varphi \right)=0$，
$\because AD=\dfrac{2\sqrt{21}}{3},\therefore {(\dfrac{\pi }{2\omega }-1)}^{2}+\dfrac{{A}^{2}{\sin}^{2}\phi }{4}=\dfrac{28}{3}$，
把$|A\sin\phi |=\dfrac{1}{\sqrt{3}}\left(2+\dfrac{\pi }{\omega }\right)$代入上式，得${(\dfrac{\pi }{\omega })}^{2}-2×\dfrac{\pi }{\omega }-24=0$，解得$\dfrac{\pi }{\omega }=6$（负值舍去），
$\therefore \omega =\dfrac{\pi }{6},\therefore \sin\left(\dfrac{\pi }{3}+\phi \right)=0$，由$|\phi |≤\dfrac{\pi }{2}$，解得$\phi =-\dfrac{\pi }{3},\therefore \sqrt{3}|A\sin\left(-\dfrac{\pi }{3}\right)|=8$，
解得$A=\dfrac{16}{3},\therefore f(x)=\dfrac{16}{3}\sin\left(\dfrac{\pi }{6}x-\dfrac{\pi }{3}\right)$，
对$\rm A$，$f\left(x\right)$的最小正周期为$\dfrac{2\pi }{\dfrac{\pi }{6}}=12$，故$\rm A$错误；
对$\rm B$：$f(8)=\dfrac{16}{3}\sin\left(\dfrac{\pi }{6}×8-\dfrac{\pi }{3}\right)=0$，故$\rm B$错误；
对$\rm C$：当$5\leqslant x\leqslant 7$时，$\dfrac{\pi }{2}≤\dfrac{\pi }{6}x-\dfrac{\pi }{3}≤\dfrac{5\pi }{6},\therefore f\left(x\right)$在$\left[5,7\right]$单调递减，故$\rm C$正确；
对$\rm D$：$f\left(-x+2\right)=\dfrac{16}{3}\sin[\dfrac{\pi }{6}\left(-x+2\right)-\dfrac{\pi }{3}]=-\dfrac{16}{3}\sin\left(\dfrac{\pi }{6}x\right)$，为奇函数，故$\rm D$正确.
故选：$\rm CD $.