已知函数$f(x)=A\sin(\omega x+\varphi )(A\gt0,\omega \gt0,0\lt\varphi \lt\pi)$的部分图象如图所示，则下列结论正确的是$(\quad\ \ \ \ )$.

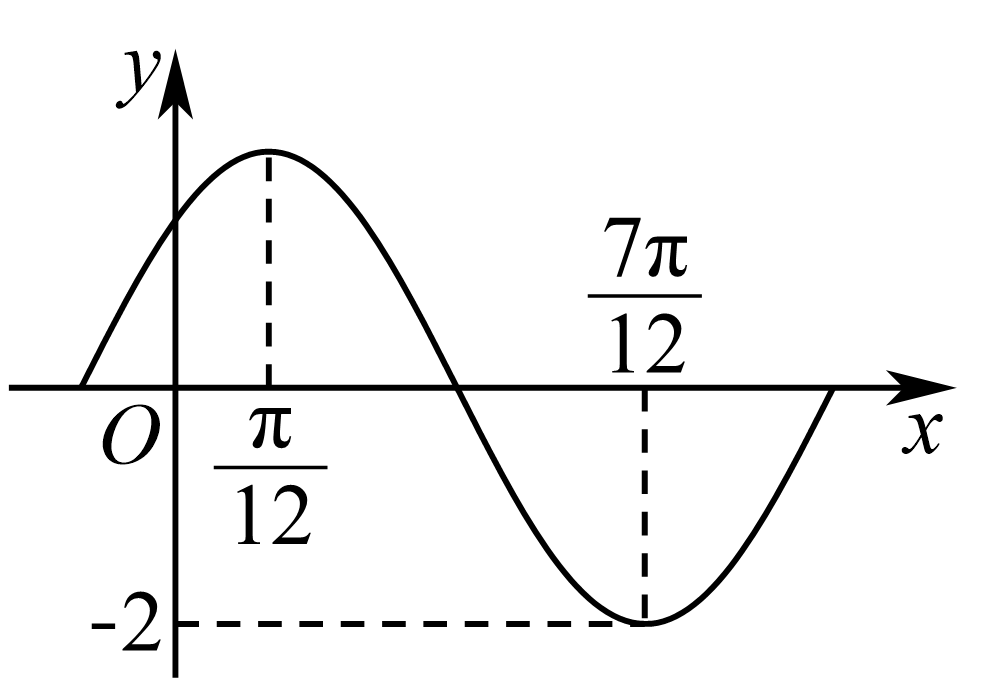
函数$f(x)$的最小正周期为$\\pi$

函数$y=f\\left( x+\\dfrac{\\pi}{6}\\right)$是偶函数

点$\\left( \\dfrac{5\\pi}{6},0\\right)$是$f(x)$图象的一个对称中心

函数$f(x)$在区间$\\left[ -\\dfrac{\\pi}{2},0\\right]$上单调递增

观察函数图象，$A = 2$，函数$f(x)$的周期$T=2\left( \dfrac{7\pi}{12}-\dfrac{\pi}{12}\right)=\pi$，$\omega=\dfrac{2\pi}{T}=2$，

又$f\left( \dfrac{\pi}{12}\right)=2$，则$2\times\dfrac{\pi}{12}+\varphi=\dfrac{\pi}{2}+2k\pi,k\in{\bf Z}$，而$0\lt\varphi\lt\pi$，于是$\varphi=\dfrac{\pi}{3}$，$f(x)=2\sin\left( 2x+\dfrac{\pi}{3}\right)$，

对于A，函数$f(x)$的最小正周期为$\pi$，A正确；

对于B，$f\left( x+\dfrac{\pi}{6}\right)=2\sin\left[ 2\left( x+\dfrac{\pi}{6}\right)+\dfrac{\pi}{3}\right]=2\sin\left( 2x+\dfrac{2\pi}{3}\right)$，函数$y=f\left( x+\dfrac{\pi}{6}\right)$不是偶函数，B错误；

对于C，$f\left( \dfrac{5\pi}{6}\right)=2\sin\left( 2\times\dfrac{5\pi}{6}+\dfrac{\pi}{3}\right)=0$，因此点$\left( \dfrac{5\pi}{6},0\right)$是$f(x)$图象的一个对称中心，C正确；

对于D，当$x\in\left[ -\dfrac{\pi}{2},0\right]$时，$2x+\dfrac{\pi}{3}\in\left[ -\dfrac{2\pi}{3},\dfrac{\pi}{3}\right]$，而当$x=-\dfrac{5\pi}{12}$时，函数$f(x)$取得最小值，

因此函数$f(x)$在区间$\left[ -\dfrac{\pi}{2},0\right]$上不单调，D错误.

故选：AC