《九章算术》是我国古代数学中的经典，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．在阳马${{P}-{ABCD}}$中，侧棱$PD\perp $底面$ABCD$，且$PD=CD=a$，点$E$是$PC$的中点，连接$DE$，$BD$，$BE$．以下结论正确的有$(\qquad)$．

$DE//$平面$PAB$

四面体$EBCD$是鳖臑

若阳马${{P}-{ABCD}}$的体积为${{V}_{1}}$，四面体$EBCD$的体积为${{V}_{2}}$，则${{V}_{1}}=4{{V}_{2}}$

若四面体$EBCD$的外接球的体积为$\\dfrac{\\sqrt{3}}{2}{{a}^{3}}$，则$CD=\\sqrt{2}AD$．

如图，取$PB$中点$F$，连接$EF$，$AF$，

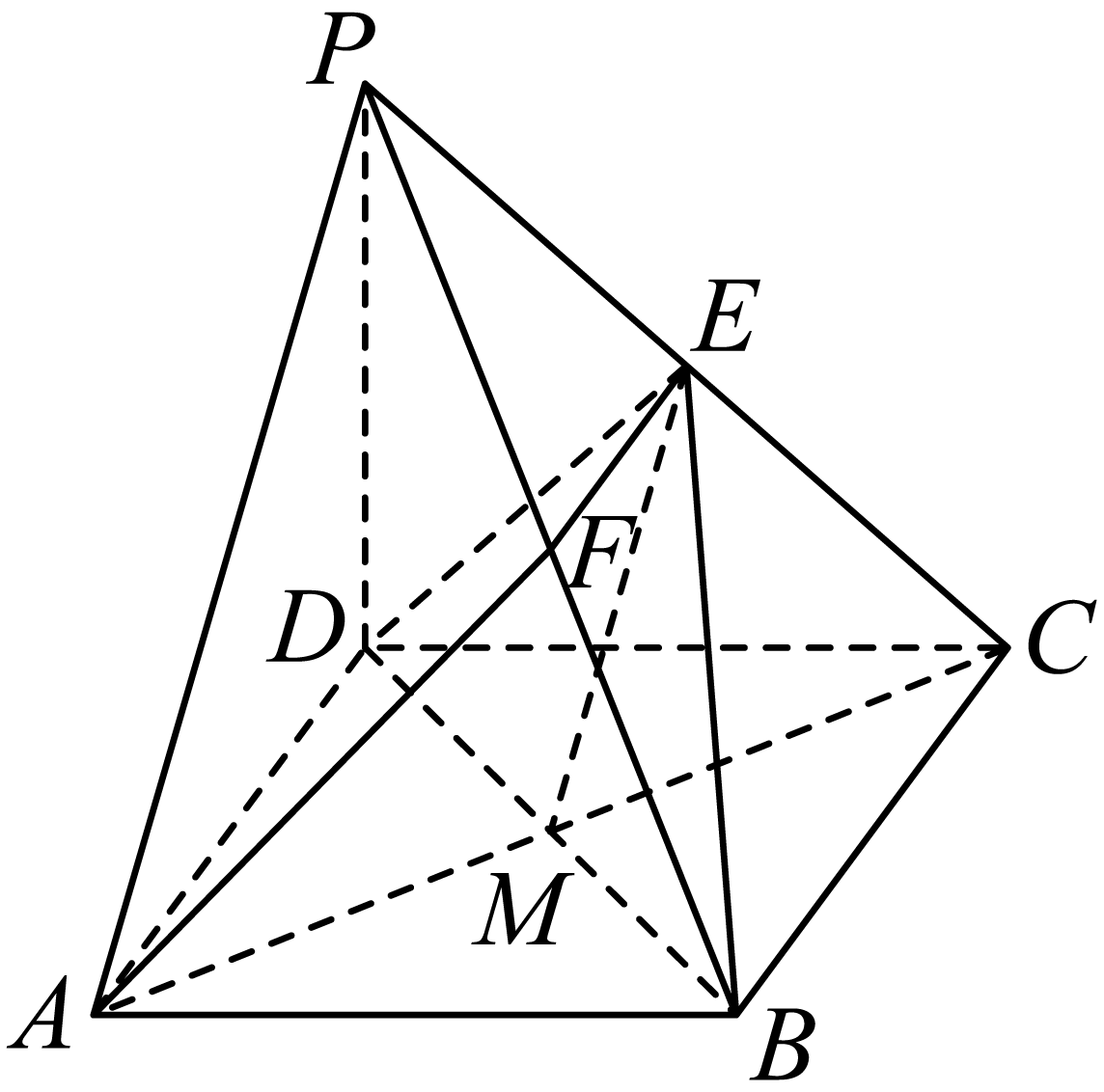
$\because E$是$PC$的中点，

$\therefore EF//BC$，$EF=\dfrac{1}{2}BC$，

$\because $ 底面$ABCD$为长方形，

$\therefore AD//BC$，$AD=BC$，

$\therefore EF//AD$，$EF=\dfrac{1}{2}AB$，

$\therefore $ 四边形$ADEF$为梯形，

$\therefore $ 直线$DE$与$AF$相交，

$\because AF\subset $平面$PAB$，

$\therefore $ 直线$DE$与平面$PAB$相交，

$\therefore \rm A$错误；

$\because PD\perp $底面$ABCD$，

$\therefore PD\perp BC$，

$\because ABCD$为长方形，

$\therefore DC\perp BC$，

$\because PD\subset PCD$,$DC\subset PCD$且$PD\cap DC=D$，

$\therefore BC\perp $平面$PCD$，

$\because DE\subset $平面$PCD$，

$\therefore BC\perp DE$，

$\because PD=CD=a$，

$\therefore DE\perp PC$，

又$BC\subset $平面$PBC$，$PC\subset $平面$PBC$，且$BC\cap PC=C$，

$\therefore DE\perp $平面$PBC$，

$\therefore $ 四面体$EBCD$四个面都是直角三角形，

$\therefore $ 四面体$EBCD$是鳖臑，

$\therefore \rm B$正确；

由题意可知${ {PD}}$是阳马${{P}-{ABCD}}$的高，

$\therefore {{V}_{1}}=\dfrac{1}{3}{{S}_{ABCD}}\cdot PD$，

$\because E$是$PC$的中点，

$\therefore {{V}_{2}}=\dfrac{1}{3}{{S}_{\triangle BCD}}\cdot \dfrac{1}{2}PD=\dfrac{1}{3}\times \dfrac{1}{2}{{S}_{ABCD}}\cdot \dfrac{1}{2}PD=\dfrac{1}{4}{{V}_{1}}$，

$\therefore \rm C$正确；

连接$AC$，则$AC$与$BD$相交与点$M$，连接$EM$，则$M$为四面体$EBCD$外接球的球心，

$\therefore $ 半径为$BM$，若$CD=\sqrt{2}AD$，则$AD=\dfrac{\sqrt{2}}{2}a$，

$\therefore BD=\sqrt{{{a}^{2}}+{{\left( \dfrac{\sqrt{2}}{2}a \right)}^{2}}}=\dfrac{\sqrt{6}}{2}a$，

$\therefore $ 四面体$EBCD$的体积$V=\dfrac{4\pi}{3}{{\left( \dfrac{1}{2}\times \dfrac{\sqrt{6}}{4}a \right)}^{3}}=\dfrac{\sqrt{6}}{64}\pi{{a}^{3}}$，

$\therefore \rm D$错误$.$  

故选：$\rm BC$