下列说法不正确的是$(\qquad)$．

有两个面平行且相似，其余各面都是梯形的多面体是棱台

如果一个棱锥的各个侧面都是等边三角形，那么这个棱锥可能为六棱锥

棱长都是$1$的三棱锥的表面积为$\\sqrt{3}$

正方体$ABCD-A_{1}B_{1}C_{1}D_{1}$的棱长为$2$，$E$，$F$分别为棱$AA_{1}$与$CC_{1}$的中点，四棱锥$A_{1}-EBFD_{1}$的体积为$\\dfrac{4}{3}$

对于$\rm A$，侧棱延长线不一定交于一点，根据棱台定义不一定是棱台，命题不正确；

对于$\rm B$，棱锥的各个侧面都是等边三角形，则顶角为$60^\circ$，

若为六棱锥，则$60^\circ \times 6=360^\circ$，为一个周角，故为平面图形，命题不正确；

对于$\rm C$，棱长都是$1$的三棱锥每个面为全等的等边三角形，

表面积为$4\times \dfrac{1}{2}\times 1\times \dfrac{\sqrt{3}}{2}=\sqrt{3}$，命题正确；

对于$\rm D$，连接$EF$，由题意，$EF//A_{1}C_{1}$，

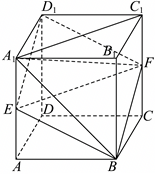
$\therefore EF\perp AA_{1}$，

则${S}_{\rm{Rt}\triangle {A}_{1}EF}=\dfrac{1}{2}{A}_{1}E\cdot EF=\dfrac{1}{2}\times 1\times 2\sqrt{2}=\sqrt{2}$，

且${V}_{{A_1}-EBF{D}_{1}}={V}_{{D_1}-{A}_{1}EF}+{V}_{B-{A_1}EF}=2{V}_{{D_1}-{A}_{1}EF}=2{V}_{F-{A_1}E{D}_{1}}=2\times \dfrac{1}{3}{S}_{\triangle {A_1}E{D}_{1}}\cdot CD$

$=2\times \dfrac{1}{3}\times \dfrac{1}{2}\times 1\times 2\times 2=\dfrac{4}{3}$，命题正确．

故选：$\rm AB$