如图，平行六面体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，底面$ABCD$是边长为$1$的正方形，$A{{A}_{1}}=\sqrt{2}$，$\angle {{A}_{1}}AD=\angle {{A}_{1}}AB=120{}^\circ $．

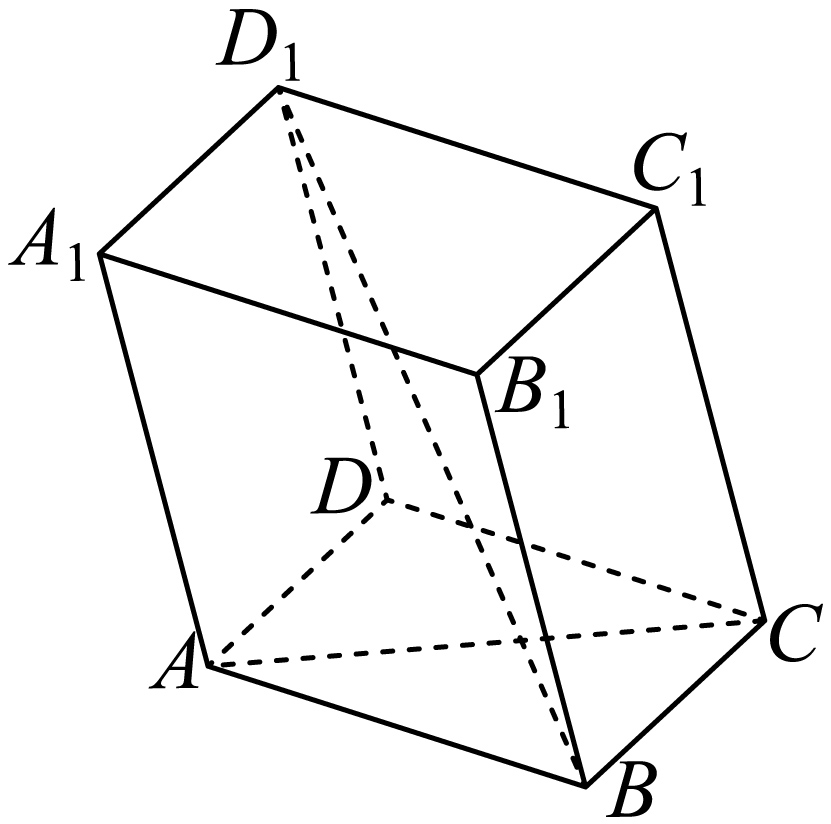
$(1)$求该平行六面体的表面积；

$(2)$记${{A}_{1}}$在底面$ABCD$上的射影为$H$，$\theta =\angle {{A}_{1}}AB$，${{\theta }_{1}}=\angle {{A}_{1}}AH$，${{\theta }_{2}}=\angle BAH$，求证：$\cos \theta =\cos {{\theta }_{1}}\cos {{\theta }_{2}}$，并求侧棱$A{{A}_{1}}$与底面$ABCD$的所成角；

$(3)$求异面直线$AC$与$B{{D}_{1}}$的所成角．

$(1)$$2\\sqrt{6}+2$；

$(2)$证明见解析，${{45}^{^\\circ }}$；

$(3)$${{60}^{^\\circ }}$

$(1)$底面$ABCD$是边长为$1$的正方形，则${{S}_{ABCD}}=1$,${{S}_{{{A1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}}}=1$,

$A{{A}_{1}}=\sqrt{2}$，$\angle {{A}_{1}}AD=\angle {{A}_{1}}AB=120{}^\circ $，

$\therefore {{S}_{侧}}=4{{S}_{{{A_1}}{{B}_{1}}AB}}=4\times 2\times \dfrac{1}{2}\left| AB \right|\cdot \left| A{{A}_{1}} \right|\cdot \sin \angle {{A}_{1}}AB=4\times \sqrt{2}\times \dfrac{\sqrt{3}}{2}=2\sqrt{6}$，

$\therefore $ 该平行六面体的表面积${{S}_{表}}={{S}_{侧}}+{{S}_{ABCD}}+{{S}_{{{A1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}}}=2\sqrt{6}+2$$.$

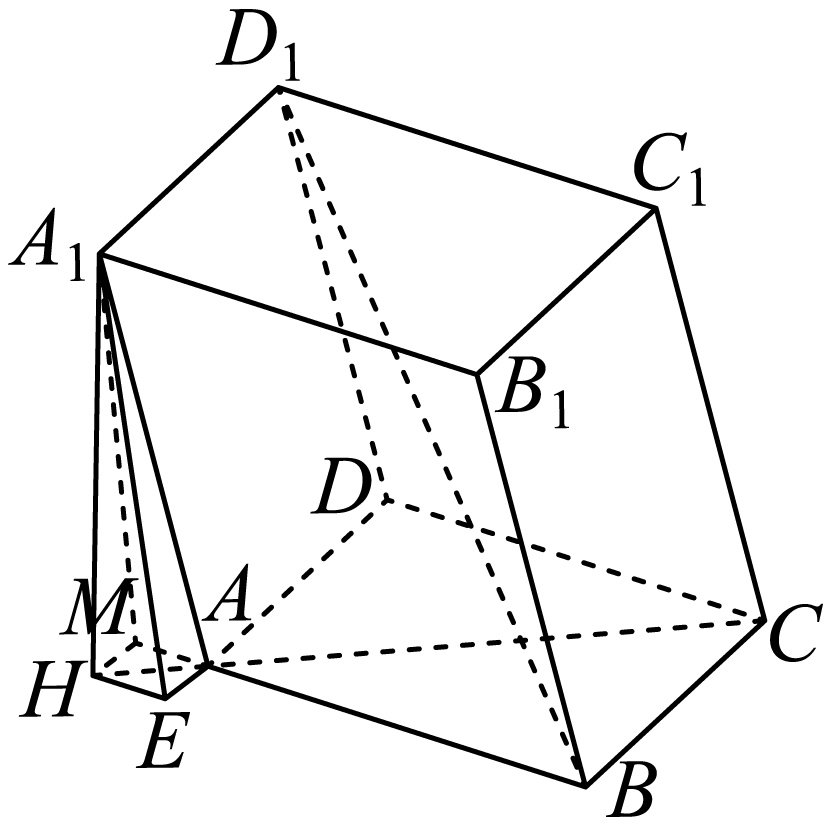
$(2)$过 ${{A}_{1}}$ 作 ${{A}_{1}}M\perp AB,{{A}_{1}}E\perp AD,{{A}_{1}}H\perp $平面$ABCD$，连接 $AM$, $HM$, $AE$, $HE$, $AH$，

此时$A D \subset$平面$ABCD$ ，${{A}_{1}}H\perp AD,{{A}_{1}}E\perp AD$，${{A}_{1}}H\cap {{A}_{1}}E={{A}_{1}}$，${{A}_{1}}H,{{A}_{1}}E\subset $平面${{A}_{1}}HE$，

$\therefore AD\perp $ 面${{A}_{1}}HE$，

$\cos \theta_1=\cos \angle A_1 A H=\dfrac{A H}{A A_1}$，$\cos \theta_2=\cos \angle B A H=-\cos \angle H A M=-\dfrac{A M}{A H}$，

$\cos \theta=-\cos \angle A_1 A M=-\dfrac{A M}{A A_1}=-\dfrac{A M}{A H} \cdot \dfrac{A H}{A A_1}=\cos \theta_1 \cos \theta_2$，得证$.$

$\because \angle {{A}_{1}}AD=\angle {{A}_{1}}AB=120{}^\circ $，则$\angle {{A}_{1}}AE=\angle {{A}_{1}}AM=60{}^\circ $,

则$AM=A{{A}_{1}}\cdot \cos 60{}^\circ =\dfrac{\sqrt{2}}{2}=AE$，

$\therefore {{A}_{1}}H=\sqrt{A{\rm A}_{1}^{2}-A{{H}^{2}}}=\sqrt{2-1}=1$ ,

$\therefore \cos \angle {{A}_{1}}AH=\dfrac{AH}{A{{A}_{1}}}=\dfrac{\sqrt{2}}{2}$，

$\therefore \angle {{A}_{1}}AH=45{}^\circ $，

$\because {{A}_{1}}H\perp $平面$ABCD$，$AH\subset $平面$ABCD$，

$\therefore {{A}_{1}}H\perp AH$，

$\therefore $ 侧棱$A{{A}_{1}}$与底面$ABCD$的所成角为$\angle {{A}_{1}}AH$$.$

$\therefore $ ，侧棱$A{{A}_{1}}$与底面$ABCD$的所成角为$45{}^\circ $$.$

$(3)$由题意$\overrightarrow{AB}\cdot \overrightarrow{AD}=0$，$\overrightarrow{A{{A}_{1}}}\cdot \overrightarrow{AB}=\overrightarrow{A{{A}_{1}}}\cdot \overrightarrow{AD}=\sqrt{2}\times 1\times \cos 120{}^\circ =-\dfrac{\sqrt{2}}{2}$，

$\overrightarrow{B{{D}_{1}}}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{D{{D}_{1}}}=-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{{A}_{1}}}$，

${{\left| \overrightarrow{B{{D}_{1}}} \right|}^{2}}={{(-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{{A}_{1}}})}^{2}}={{\overrightarrow{AB}}^{2}}+{{\overrightarrow{AD}}^{2}}+{{\overrightarrow{A{{A}_{1}}}}^{2}}-2\overrightarrow{AB}\cdot \overrightarrow{AD}-2\overrightarrow{AB}\cdot \overrightarrow{A{{A}_{1}}}+2\overrightarrow{AD}\cdot \overrightarrow{A{{A}_{1}}}$

$=1+1+2-0-2\times \left( -\dfrac{\sqrt{2}}{2} \right)+2\times \left( -\dfrac{\sqrt{2}}{2} \right)=4$，

$\therefore B{{D}_{1}}=\left| \overrightarrow{B{{D}_{1}}} \right|=2$．

而$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$，$\left| \overrightarrow{AC} \right|=\sqrt{2}$，

则$\overrightarrow{B{{D}_{1}}}\cdot \overrightarrow{AC}=(-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{A{{A}_{1}}})\cdot (\overrightarrow{AB}+\overrightarrow{AD})={{\overrightarrow{AD}}^{2}}-{{\overrightarrow{AB}}^{2}}+\overrightarrow{A{{A}_{1}}}\cdot \overrightarrow{AB}+\overrightarrow{A{{A}_{1}}}\cdot \overrightarrow{AD}$

$=1-1+\left( -\dfrac{\sqrt{2}}{2} \right)+\left( -\dfrac{\sqrt{2}}{2} \right)=-\sqrt{2}$，

$\therefore \left| \cos \left\langle \overrightarrow{B{{D}_{1}}},\overrightarrow{AC} \right\rangle \right|=\dfrac{\left| \overrightarrow{B{{D}_{1}}}\cdot \overrightarrow{AC} \right|}{\left| \overrightarrow{B{{D}_{1}}} \right|\left| \overrightarrow{AC} \right|}=\dfrac{\sqrt{2}}{2\times \sqrt{2}}=\dfrac{1}{2}$，

$\therefore $ 直线$B{{D}_{1}}$与$AC$所成角为${{60}^{^\circ }}$$.$