正方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$棱长为$4$，点$P$满足$\left| \overrightarrow{PB} \right|=1$，点$Q$满足$\overrightarrow{AQ}=\lambda \overrightarrow{AD}+\left( 1-\lambda \right)\overrightarrow{A{{D}_{1}}}$，$\lambda \in \bf{R}$，则$\left| \overrightarrow{AP}+\overrightarrow{AQ} \right|$的最小值为                 $.$

如图建立空间直角坐标系：

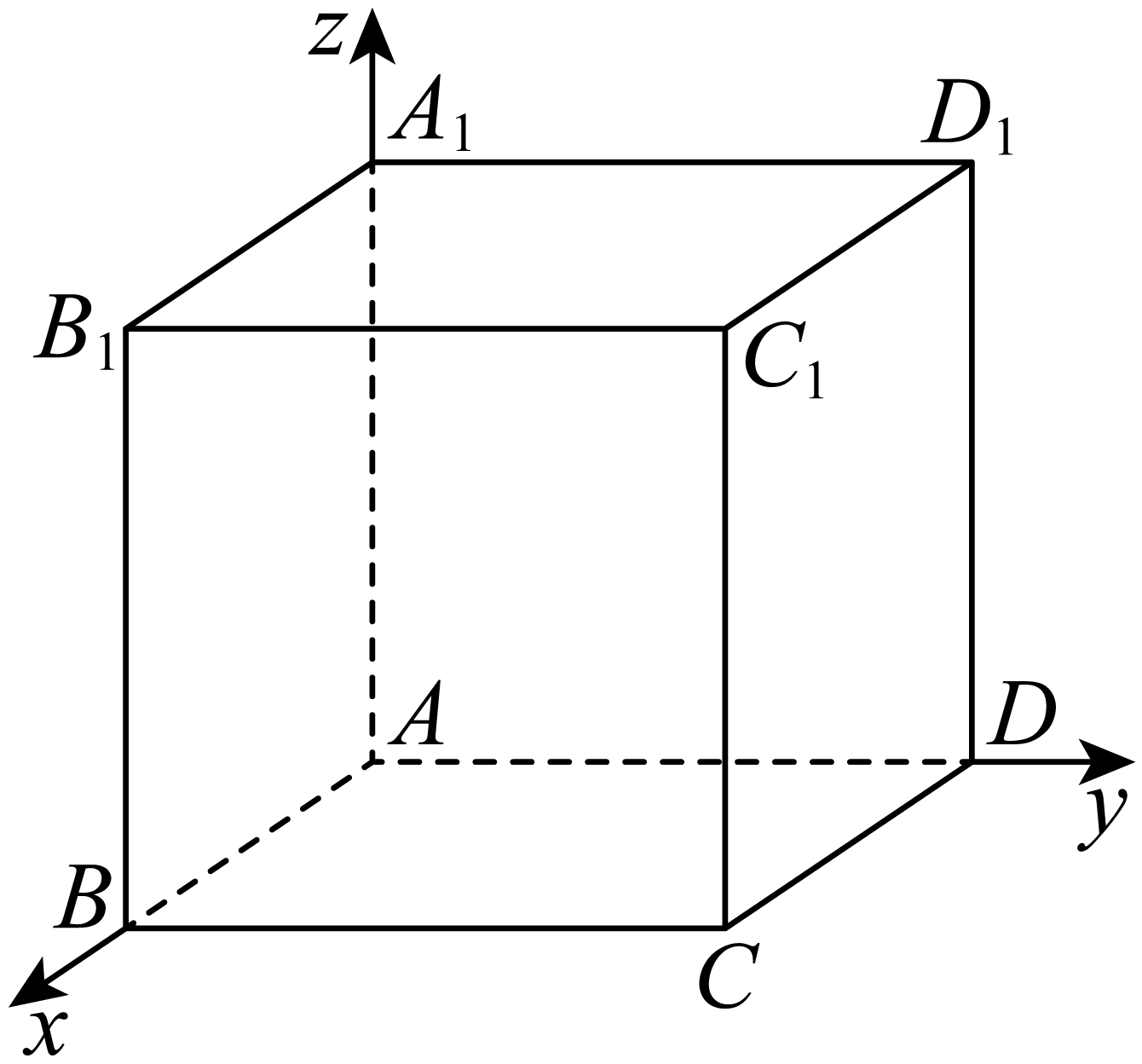
则由题意可得$A\left( 0,0,0 \right)$，$B\left( 4,0,0 \right)$，$D\left( 0,4,0 \right)$，${{D}_{1}}\left( 0,4,4 \right)$$.$

$\because $ 点$Q$满足$\overrightarrow{AQ}=\lambda \overrightarrow{AD}+\left( 1-\lambda \right)\overrightarrow{A{{D}_{1}}}$，$\lambda \in \bf{R}$，

$\therefore $ 点$Q$，点$D$和点${{D}_{1}}$三点共线$.$

设$P\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)$，$Q\left( 0,4,t \right)$，

则$\overrightarrow{AP}=\left( {{x}_{0}},{{y}_{0}},{{z}_{0}} \right)$，$\overrightarrow{AQ}=\left( 0,4,t \right)$，

$\therefore \overrightarrow{AP}+\overrightarrow{AQ}=\left( {{x}_{0}},{{y}_{0}}+4,{{z}_{0}}+t \right)$

则$\left| \overrightarrow{AP}+\overrightarrow{AQ} \right|=\sqrt{x_{0}^{2}+{{\left( {{y}_{0}}+4 \right)}^{2}}+{{\left( {{z}_{0}}+t \right)}^{2}}}$$.$

令$y=x_{0}^{2}+{{\left( {{y}_{0}}+4 \right)}^{2}}+{{\left( {{z}_{0}}+t \right)}^{2}}$，则该函数可以看做是关于$t$的二次函数，

则当$t=-{{z}_{0}}$时，函数$y=x_{0}^{2}+{{\left( {{y}_{0}}+4 \right)}^{2}}+{{\left( {{z}_{0}}+t \right)}^{2}}$有最小值，为$\sqrt{x_{0}^{2}+{{\left( {{y}_{0}}+4 \right)}^{2}}}$$.$

$\therefore $ 要使$\left| \overrightarrow{AP}+\overrightarrow{AQ} \right|$最小，可先取$t=-{{z}_{0}}$，此时$\left| \overrightarrow{AP}+\overrightarrow{AQ} \right|=\sqrt{x_{0}^{2}+{{\left( {{y}_{0}}+4 \right)}^{2}}}$，

其几何意义是点$P$在平面$xoy$上的射影点${{P}_{0}}\left( {{x}_{0}},{{y}_{0}},0 \right)$到点$M\left( 0,-4,0 \right)$的距离$.$

又$\because \left| \overrightarrow{PB} \right|=1$，

$\therefore $ 点$P$的轨迹是以点$B\left( 4,0,0 \right)$为球心，$1$为半径的球面，

则射影点${{P}_{0}}\left( {{x}_{0}},{{y}_{0}},0 \right)$的轨迹是以点$B\left( 4,0,0 \right)$为圆心，$1$为半径的圆及其内部$.$

$\therefore\left| \overrightarrow{AP}+\overrightarrow{AQ}\right|=\sqrt{x_{0}^{2}+\left( y_{0}+4\right)^{2}}\geqslant\left| BM\right|-1$

又$\because \left| BM \right|=\sqrt{{{\left( 4-0 \right)}^{2}}+{{\left[ 0-\left( -4 \right) \right]}^{2}}+{{\left( 0-0 \right)}^{2}}}=4\sqrt{2}$，

$\therefore\left| \overrightarrow{AP}+\overrightarrow{AQ}\right|\geqslant4\sqrt{2}-1$．

故答案为：$4\sqrt{2}-1$