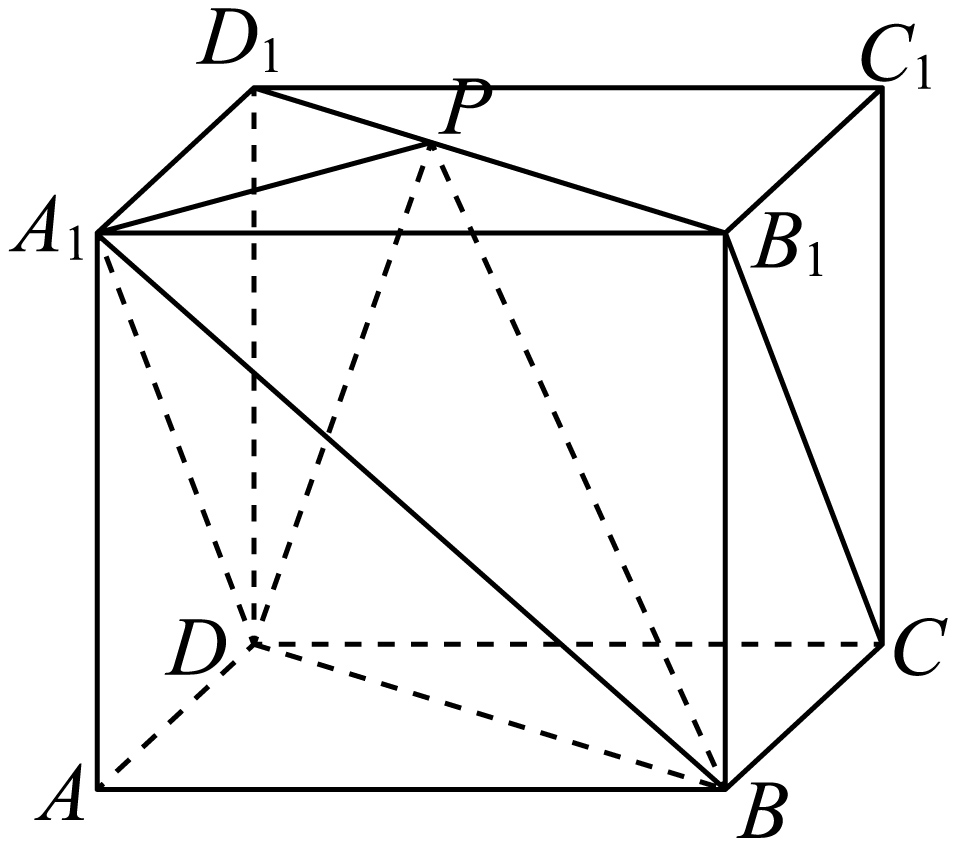
如图，长方体$ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$中，$AB=2$，$AD=1$，$A{{A}_{1}}=2$，$O$为底面$ABCD$的中心，点$P$为${{D}_{1}}{{B}_{1}}$上的动点（包括端点），则当$\triangle P{{A}_{1}}O$的面积最小时，线段$DP$的长为                 ．

如图以$DA,DC,D{{D}_{1}}$所在的直线分别为$x,y,z$轴建立空间直角坐标系，则

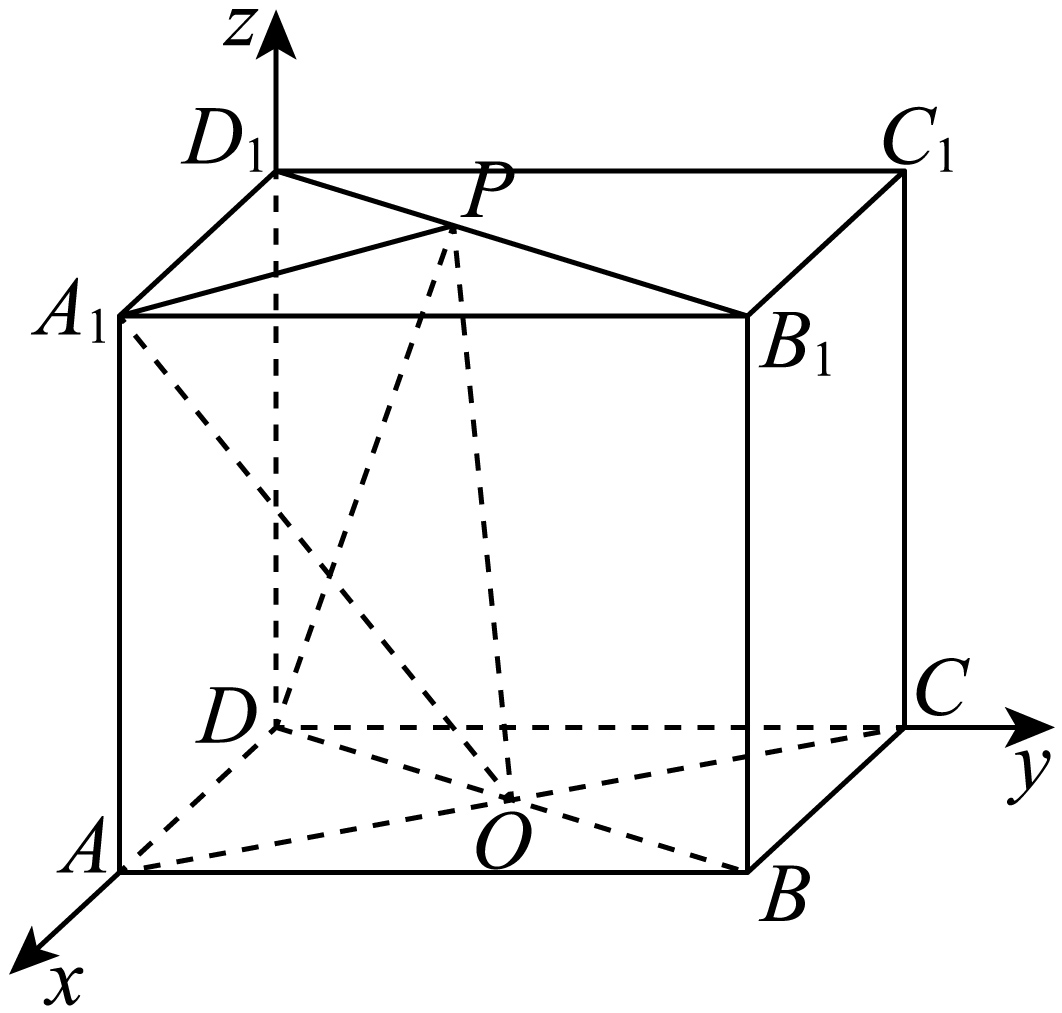
$D(0,0,0),{{A}_{1}}(1,0,2),O\left(\dfrac{1}{2},1,0\right)$，${{D}_{1}}(0,0,2),{{B}_{1}}(1,2,2)$，

则$\overrightarrow{{{A}_{1}}O}=\left( -\dfrac{1}{2},1,-2 \right),\overrightarrow{{{D}_{1}}{{B}_{1}}}=(1,2,0)$，

设$P(a,b,2)$，则$\overrightarrow{{{D}_{1}}P}=(a,b,0)$，

$\because \overrightarrow{{{D}_{1}}P}$‖$\overrightarrow{{{D}_{1}}{{B}_{1}}}$，

$\therefore \dfrac{a}{1}=\dfrac{b}{2}$，得$b=2a$，

$\therefore P(a,2a,2)$$($$0\le a\le 1$$)$，则$\overrightarrow{{{A}_{1}}P}=(a-1,2a,0)$，

设点$P$到${{A}_{1}}O$的距离为$d$，则

${{d}^{2}}={{\left| \overrightarrow{{{A}_{1}}P} \right|}^{2}}-{{\left( \dfrac{\overrightarrow{{{A}_{1}}P}\cdot \overrightarrow{{{A}_{1}}O}}{\left| \overrightarrow{{{A}_{1}}O} \right|} \right)}^{2}}={{(a-1)}^{2}}+4{{a}^{2}}-\dfrac{{{\left[-\dfrac{1}{2}(a-1)+2a\right]}^{2}}}{\dfrac{1}{4}+1+4}$

$=5{{a}^{2}}-2a+1-\dfrac{{{\left(\dfrac{3}{2}a+\dfrac{1}{2}\right)}^{2}}}{\dfrac{21}{4}}$

$=5{{a}^{2}}-2a+1-\dfrac{{{(3a+1)}^{2}}}{21}$

$=\dfrac{96{{a}^{2}}-48a+20}{21}$，

$\therefore $ 当$a=-\dfrac{-48}{2\times 96}=\dfrac{1}{4}$时，$d$取得最小值，此时$\triangle P{{A}_{1}}O$的面积取得最小值，

$\therefore P\left(\dfrac{1}{4},\dfrac{1}{2},2\right)$，

$\therefore DP=\sqrt{\dfrac{1}{16}+\dfrac{1}{4}+4}=\dfrac{\sqrt{69}}{4}$．

故答案为：$\dfrac{\sqrt{69}}{4}$